R1 2008 høst LØSNING

a)

1)<tex>f(x)=3e^{2x}, \quad f'(x) = 3 \cdot 2 e^{2x} = 6e^{2x}</tex>

2)<tex>h(x)=x \cdot lnx, \quad h'(x) = lnx + x \cdot \frac 1x = lnx + 1 </tex>

b)

l går gjennom A(1,2) og B(3,7), <tex> \vec{AB}=[2,5]</tex>

1)Parameterfremmstilling:<tex> l: \left [ x = 1+2t \\ y = 2 + 5t \right]</tex>

2) Skjæring med x-akse, y = 0:<tex>t = - \frac 25 \Rightarrow x = \frac 15, \quad \quad ( \frac 15,0)</tex>

Skjæring med y-akse, x = 0:<tex>t = - \frac 12 \Rightarrow y = -\frac 12, \quad \quad (0,- \frac 12)</tex>

c)

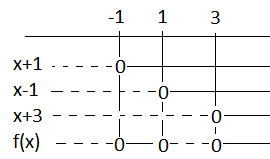
1)<tex>f(-1) = (-1)^3 - 3 \cdot (-1)^2 - (-1)+3 = -1-3+1+3 = 0 \quad</tex> dvs.f(x) er delelig med (x-(-1))

<tex>\quad \quad x^3-3x^2-x+3: (x+1) = x^2-4x+3 \\ -(x^3 +x^2) \\ \quad \quad\quad\quad \quad -4x^2-x \\ \quad \quad -(-4x^2-4x) \\ \quad \quad\quad \quad\quad \quad\quad \quad\quad \quad -(3x+3)\\ \quad \quad\quad \quad \quad \quad\quad \quad\quad \quad\quad \quad\quad\quad \quad \quad 0 </tex>

<tex>x^2-4x+3 = 0 \\ x= \frac {4 \pm \sqrt{16-12}}{2} = \frac{4 \pm 2}{2} \\ x = 1 \vee x=3 \\ f(x)= x^3-3x^2-x+3 = (x+1)(x-1)(x-3)</tex>

2)

<tex>f(x) \geq 0 \\ x \in [-1,1] \cup [3,\rightarrow></tex>

d)

1) Lengden av sidene i trekanten: <tex>\vec{AB}= [2,1], \vec{BC} =[-1,4], \vec{AC} = [1,5] \\ AB = \sqrt{5},\quad BC = \sqrt{17},\quad AC=\sqrt{26}</tex>

2)

Dersom trekanten er rettvinklet må AC være hypotenusen.

<tex>(AC)^2 = 26 \\ (AB)^2 + (AC)^2 = 5+17 = 22 </tex>

Trekanten er ikke rettvinklet.

e)

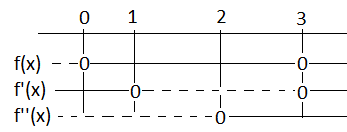
1)grafen til f(x) er heltrukket og grafen til f'(x) er stipplet. f(x) vokser til x = 1 hvor den har et maksimum. Fra x = 1 til x = 3 er f(x) avtagende, med et minimum i x = 3. Den deriverte er null i x = 1 og x = 3 og negativ mellom disse verdiene, som er i samsvar med at grafen til f har et negativt stigningstall i dette området. Der f vokser er f' positiv.

2)

a)

<tex> \vec{OB}= [3,0], \vec{OC}= [4,3], \vec{OD}= [-1,5] \\ \vec{OM_1}= \frac 12 \vec{OB}= [ \frac 32,0] \\ \vec{OM_2}= \frac12 \vec{OB}+ \fra 12\vec{OC}= [\frac 32,0]+[2, \frac 32] =[\frac 72,\frac 32] \\ \vec{OM_3}=\frac 12\vec{OC}+\frac 12 \vec{OD}= [2, \frac32]+[- \frac 12, \frac 52]=[\frac 32,4] \\ \vec{OM_4}= \frac 12\vec{OD}=[-\frac 12, \frac 52]</tex>

b)

Dersom firkanten <tex>M_1M_2M_3M_4</tex> er et parallellogram, må <tex> \vec{M_1M_2} =\vec{M_4M_3} </tex>:

<tex> \vec{M_1M_2} = [\frac 72, \frac 32]-[\frac 32,0]=[2, \frac32]\\ \vec{M_4M_3}= [\frac 32,4]-[- \frac 12, \frac 52]=[2, \frac32] </tex>

Man observerer at så er tilfelle og at firkanten derfor er et parallellogram.

c)

Dersom firkanten <tex>N_1N_2N_3N_4</tex> er et parallellogram, må <tex> \vec{N_1N_2} =\vec{N_4N_3} </tex>:

<tex> \vec{N_1N_2} = [\frac{a+b}{2} \quad ,\quad \frac {c}{2}]-[\frac a2\quad,\quad0]=[\frac b2\quad, \quad\frac c2]\\ \vec{N_4N_3}= [\frac{b+d}{2}\quad,\quad\frac{c+e}{2}]-[ \frac d2\quad,\quad \frac e2]=[\frac b2\quad, \quad\frac c2] </tex>

DEL TO

b)

<tex>P()= \frac{ \left ({16}\\{7} \right)\cdot\left ({14}\\{3} \right) }{\left ({30}\\{10} \right)} = 0,139 </tex>