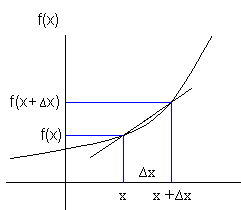Forskjell mellom versjoner av «Derivasjon»
(Ny side: Nedenfor følger en oversikt over de vanligste derivasjonsreglene for funksjoner med en variabel.<p> <table border="1" cellpadding="10"> <tr> <td>'''TYPE'''</td> <td>'''FUNKSJO...) |
|||
| (4 mellomliggende revisjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
| + | == Definisjon == | ||
| + | |||
| + | |||
| + | Den deriverte av en funksjon beskriver hastigheten funksjonene forandrer seg med, med hensyn på en uavhengig variabel. Den deriverte er også stigningen til tangenten av kurven. La oss anta at vi har funksjonen f(x) i et koordinatsystem. Vi velger et punkt x på førsteaksen. Tilhørende funksjonsverdi er f(x). La oss tenke oss at vi beveger oss et lite stykke bortover på førsteaksen fra x. Denne avstanden kaller vi ∆x. Dette nye punktet på førsteaksen heter da x+∆x. Funksjonsverdien til dette punktet blir f(x+∆x). Dette kan se slik ut:<p></p> | ||
| + | [[Bilde:Diferens.gif]]<p></p> | ||
| + | Om vi så tenker oss at størrelsen på ∆x går mot null har vi følgende: | ||
| + | <p></p> | ||
| + | <math>f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} </math> | ||
| + | |||
| + | Den deriverte av f(x) skrives f '(x) og er gitt ved uttrykket over. Vi se at stigningstallet til sekanten vil nærme seg stigningstallet til grafens tangent i x, når ∆x går mot null. | ||
| + | |||
| + | == Derivasjonsregler == | ||
Nedenfor følger en oversikt over de vanligste derivasjonsreglene for funksjoner med en [[variabel]].<p> | Nedenfor følger en oversikt over de vanligste derivasjonsreglene for funksjoner med en [[variabel]].<p> | ||
| Linje 15: | Linje 27: | ||
<td>f(x) = x<sup>n</sup></td> | <td>f(x) = x<sup>n</sup></td> | ||
<td>f '(x) = nx<sup>n-1</sup></td> | <td>f '(x) = nx<sup>n-1</sup></td> | ||
| − | <td>< | + | <td><math>(x^3)' = 3x^2</math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Linje 22: | Linje 34: | ||
<td> c f(x) </td> | <td> c f(x) </td> | ||
<td>[c f(x)]' = c f '(x) </td> | <td>[c f(x)]' = c f '(x) </td> | ||
| − | <td>< | + | <td><math>(4x^3)' = 4 \cdot 3x^2 = 12x^2</math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Linje 34: | Linje 46: | ||
<td> f(x) = g(x)+ h(x) +... </td> | <td> f(x) = g(x)+ h(x) +... </td> | ||
<td> f '(x) = g'(x) + h'(x) +... </td> | <td> f '(x) = g'(x) + h'(x) +... </td> | ||
| − | <td>< | + | <td><math>(x^3 -4x^2 +2x -1)' = 3x^2 - 8x + 2</math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Linje 49: | Linje 61: | ||
<tr> | <tr> | ||
<td>Produkt<br>[[Bevis]]<br>[[Eksempel på derivasjon med produktregelen|Eksempel]]<br>Se video [http://youtu.be/t6Lu4vDVfhg]</td> | <td>Produkt<br>[[Bevis]]<br>[[Eksempel på derivasjon med produktregelen|Eksempel]]<br>Se video [http://youtu.be/t6Lu4vDVfhg]</td> | ||
| − | <td> f(x)< | + | <td> f(x)<math>\cdot</math>g(x) </td> |
| − | <td> [f(x)< | + | <td> [f(x)<math>\cdot</math>g(x)]'= f '(x)<math>\cdot</math>g(x)+ f(x)<math>\cdot</math>g '(x) </td> |
| − | <td> < | + | <td> <math>(4x^3cos(x))'= 12x^2cos(x)-4x^3sin(x) \\ = 4x^2(3cos(x)-xsin(x))</math> </td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| Linje 66: | Linje 78: | ||
<td> Tangens </td> | <td> Tangens </td> | ||
<td> f (x) = tan x</td> | <td> f (x) = tan x</td> | ||
| − | <td> < | + | <td> <math>f ' (x)=\frac{1}{cos^2x}</math> eller <math> f ' (x)= 1 + tan^2x </math> </td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td> Kvotient </td> | <td> Kvotient </td> | ||
| − | <td> f (x)=< | + | <td> f (x)=<math>\frac{g(x)}{h(x)}</math> |
| − | <td> f ' (x)=< | + | [[Bevis]] </td> |
| − | <td>< | + | <td> f ' (x)=<math>\frac{g ' (x)\cdot h(x)- g(x)\cdot h ' (x)}{(h(x))^2}</math> </td> |
| + | <td><math>( \frac{sin x}{2x^3})' \\ = \frac{cosx \cdot 2x^3 - 6x^2sinx}{4x^6}\\ = \frac{xcosx-3sinx}{2x^4}</math> </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Linje 78: | Linje 91: | ||
<td>y = g(u)<br>u er en funksjon av x </td> | <td>y = g(u)<br>u er en funksjon av x </td> | ||
<td>y ' = g ' (u)∙u' </td> | <td>y ' = g ' (u)∙u' </td> | ||
| − | <td>< | + | <td><math>(sin(x^2))' = 2x cos(x^2)</math> </td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Logaritme funksjonen </td> | <td>Logaritme funksjonen </td> | ||
<td> f(x) = ln |x|</td> | <td> f(x) = ln |x|</td> | ||
| − | <td> f ' (x)=< | + | <td> f ' (x)=<math>\frac{1}{x}</math> </td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Kvadratrot </td> | <td>Kvadratrot </td> | ||
| − | <td> f(x)=< | + | <td> f(x)=<math>\sqrt{x}</math> </td> |
| − | <td> f ' (x)=< | + | <td> f ' (x)=<math>\frac{1}{2\sqrt{x}}</math> </td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Nte'rot </td> | <td>Nte'rot </td> | ||
| − | <td> f(x)=< | + | <td> f(x)=<math>\sqrt[m]{x^n}=x^{\frac{n}{m}}</math> </td> |
| − | <td> Se potensfunksjon | + | <td> Se potensfunksjon </td> |
</tr> | </tr> | ||
Nåværende revisjon fra 23. mar. 2019 kl. 21:57
Definisjon
Den deriverte av en funksjon beskriver hastigheten funksjonene forandrer seg med, med hensyn på en uavhengig variabel. Den deriverte er også stigningen til tangenten av kurven. La oss anta at vi har funksjonen f(x) i et koordinatsystem. Vi velger et punkt x på førsteaksen. Tilhørende funksjonsverdi er f(x). La oss tenke oss at vi beveger oss et lite stykke bortover på førsteaksen fra x. Denne avstanden kaller vi ∆x. Dette nye punktet på førsteaksen heter da x+∆x. Funksjonsverdien til dette punktet blir f(x+∆x). Dette kan se slik ut:
Om vi så tenker oss at størrelsen på ∆x går mot null har vi følgende:
<math>f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} </math>
Den deriverte av f(x) skrives f '(x) og er gitt ved uttrykket over. Vi se at stigningstallet til sekanten vil nærme seg stigningstallet til grafens tangent i x, når ∆x går mot null.
Derivasjonsregler
Nedenfor følger en oversikt over de vanligste derivasjonsreglene for funksjoner med en variabel.
| TYPE | FUNKSJON | DERIVERT | EKSEMPEL |
| Potenser |
f(x) = xn | f '(x) = nxn-1 | <math>(x^3)' = 3x^2</math> |
| Konstant multiplisert med funksjon |
c f(x) | [c f(x)]' = c f '(x) | <math>(4x^3)' = 4 \cdot 3x^2 = 12x^2</math> |
| Konstant | f(x)= C | C' = 0 | (5)' = 0 |
| Polynom | f(x) = g(x)+ h(x) +... | f '(x) = g'(x) + h'(x) +... | <math>(x^3 -4x^2 +2x -1)' = 3x^2 - 8x + 2</math> |
| Eksponentialfunksjonen ax | f (x) = ax | f '(x) = axln a | |
| Eksponentialfunksjonen ex | f (x) = ex | f '(x) = ex | |
| Produkt Bevis Eksempel Se video [1] |
f(x)<math>\cdot</math>g(x) | [f(x)<math>\cdot</math>g(x)]'= f '(x)<math>\cdot</math>g(x)+ f(x)<math>\cdot</math>g '(x) | <math>(4x^3cos(x))'= 12x^2cos(x)-4x^3sin(x) \\ = 4x^2(3cos(x)-xsin(x))</math> |
| Sinus | f(x) = sin x | f'(x) = cos x | |
| Cosinus | f(x) = cos x | f'(x) = -sin x | |
| Tangens | f (x) = tan x | <math>f ' (x)=\frac{1}{cos^2x}</math> eller <math> f ' (x)= 1 + tan^2x </math> | |
| Kvotient | f (x)=<math>\frac{g(x)}{h(x)}</math> Bevis | f ' (x)=<math>\frac{g ' (x)\cdot h(x)- g(x)\cdot h ' (x)}{(h(x))^2}</math> | <math>( \frac{sin x}{2x^3})' \\ = \frac{cosx \cdot 2x^3 - 6x^2sinx}{4x^6}\\ = \frac{xcosx-3sinx}{2x^4}</math> |
| Kjerneregel | y = g(u) u er en funksjon av x |
y ' = g ' (u)∙u' | <math>(sin(x^2))' = 2x cos(x^2)</math> |
| Logaritme funksjonen | f(x) = ln |x| | f ' (x)=<math>\frac{1}{x}</math> | |
| Kvadratrot | f(x)=<math>\sqrt{x}</math> | f ' (x)=<math>\frac{1}{2\sqrt{x}}</math> | |
| Nte'rot | f(x)=<math>\sqrt[m]{x^n}=x^{\frac{n}{m}}</math> | Se potensfunksjon |