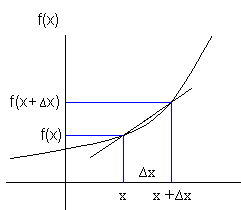Derivasjon

Gjennomsnittlig vekst

Gjennomsnittlig vekst refererer til den jevne eller gjennomsnittlige økningen (eller reduksjonen) i en verdi over en bestemt tidsperiode. Dette konseptet brukes ofte i matematikk, økonomi og naturfag for å forstå utviklingen over tid, og det gir et mål på hvordan en variabel forandrer seg i gjennomsnitt mellom to punkter.

Matematisk beregnes gjennomsnittlig vekst ved hjelp av formelen:

\[ \text{Gjennomsnittlig vekst} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} \]

Her er:

\( y_1 \) og \( y_2 \): verdier ved to forskjellige tidspunkter \( x_1 \) og \( x_2 \),

\( \Delta y \): forskjellen mellom de to verdiene,

\( \Delta x \): forskjellen mellom de to tidspunktene.

Eksempel: Gjennomsnittlig vekst i et tre

La oss si at et tre er 2 meter høyt når det blir plantet, og etter 5 år har det vokst til en høyde på 7 meter. Vi ønsker å finne ut hva den gjennomsnittlige veksten per år er.

Steg 1: Identifiser verdiene

Startverdi (\( y_1 \)): 2 meter (ved \( x_1 = 0 \), altså år 0).

Sluttverdi (\( y_2 \)): 7 meter (ved \( x_2 = 5 \), altså år 5).

Steg 2: Beregn forskjellene

\( \Delta y = y_2 - y_1 = 7 - 2 = 5 \) meter.

\( \Delta x = x_2 - x_1 = 5 - 0 = 5 \) år.

Steg 3: Sett inn i formelen

\[ \text{Gjennomsnittlig vekst} = \frac{\Delta y}{\Delta x} = \frac{5 \, \text{meter}}{5 \, \text{år}} = 1 \, \text{meter per år}. \]

Tolkning: Det betyr at treet har vokst i gjennomsnitt 1 meter per år over de fem årene. Den blå grafen viser modellen for vekst. Vi ser at treet vokser sakte i starten, og at vekstfarten øker etter hvert. Den røde stiplede linjen viser den gjennomsnittlige vekstfarten i perioden 0 til 5 år.

Dersom vi trenger å vite hva veksten var på et gitt tidspunkt, bruker vi det som kalles for momentan vekst.

Gjennomsnittlig vekst gir en enkel måte å forstå endring over tid på, selv om veksten i virkeligheten kanskje ikke har vært helt jevn. Dette gjør konseptet nyttig i alt fra biologiske studier til økonomiske analyser.

Momentan vekst

Den momentane veksten i et punkt er det samme som den deriverte i punktet.

Momentan vekst refererer til vekstraten i et bestemt øyeblikk i stedet for gjennomsnittet over en periode. Der gjennomsnittlig vekst måler endringen mellom to punkter, beskriver momentan vekst hva som skjer "akkurat nå". Matematikere bruker den deriverte til å beregne momentan vekst, som er et sentralt konsept i kalkulus.

Matematisk kan momentan vekst defineres som grensen for gjennomsnittlig vekst når tidsintervallet \( \Delta x \) nærmer seg 0. Dette skrives som:

\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

Her er:

- \( f'(x) \): den momentane vekstraten,

- \( f(x) \): funksjonsverdien (f.eks. høyden på et tre, en mengde penger, eller en annen variabel),

- \( \Delta x \): et lite tidsintervall.

Den deriverte av en funksjon beskriver hastigheten funksjonene forandrer seg med, med hensyn på en uavhengig variabel. Den deriverte er også stigningen til tangenten av kurven. La oss anta at vi har funksjonen f(x) i et koordinatsystem. Vi velger et punkt x på førsteaksen. Tilhørende funksjonsverdi er f(x). La oss tenke oss at vi beveger oss et lite stykke bortover på førsteaksen fra x. Denne avstanden kaller vi ∆x. Dette nye punktet på førsteaksen heter da x+∆x. Funksjonsverdien til dette punktet blir f(x+∆x).

Gjennomsnittlig vekst gir et mål på endringen over en periode, mens momentan vekst forteller oss hvor raskt verdien endrer seg på et spesifikt tidspunkt. For å forstå forskjellen kan vi sammenligne det med å kjøre bil: gjennomsnittshastigheten forteller hvor raskt du har kjørt i gjennomsnitt over hele turen, mens momentan hastighet forteller hvor raskt du kjører på et spesifikt tidspunkt – som målt med en fartsmåler.

---

Eksempel: Momentan vekst av et tre

La oss si at høyden til et tre \( h(t) \) (i meter) er gitt av funksjonen \( h(t) = 0,2t^2 + 2 \), der \( t \) er tiden i år. Vi ønsker å finne den momentane vekstraten (veksthastigheten) etter \( t = 1 \) år, og etter \(t =4,5\) år. (Dette er samme treet som vi så på i gjennomsnittlig vekst.)

Steg 1: Finn den deriverte av \( f(t) \)

Den momentane vekstraten er gitt av den deriverte \( f'(t) \). Deriver funksjonen: \[ f'(t) =( 0,2t^2 + 2)' = 0,4t \]

Steg 2: Beregn \( f'(t) \) ved \( t = 1 \) og \( t=4,5\) Sett inn i \( f'(t) \): \[ f'(1) = 0,4 \cdot 1 = 0,4 \] \[ f'(4,5) = 0,4 \cdot 4,5 = 1,8 \]

Tolkning: Den momentane vekstraten etter 1 år er 0,4 meter per år. Det betyr at treet vokser med en hastighet på 0,4 meter per år akkurat på dette tidspunktet. Etter 4,5 år er veksten bedre, da er den 1,8 m/år. Legg merke til at den deriverte i punktene er stigningstallet til tangenten i det respektive punkt.

Sammenligning med gjennomsnittlig vekst

Hvis vi sammenligner dette med gjennomsnittlig vekst mellom \( t = 0 \) og \( t = 5 \), så vi at den var 1,0 m/år. Det er en grei informasjon dersom vi ikke er enteressert i detaljene i vekstforløpet, men bare gjennomsnittet mellom start og stopp punkt. Skal man si noe mer detaljert om veksten er ofte momentan vekst egnet til det.

Dersom man ikke har et funksjonsuttrykk, men bare en graf kan man likevel finne gode verdier for både gjennomsnittlig vekst og momentan vekst.

For gjennomsnittlig vekst: Merk av start og sluttpunkt på grafen. Legg en linjal over og tegn den rette linjen mellom punktene. Finn stigningstallet til den rette linjen. Det er den gjennomsnittlige veksten.

For momentan vekst: Merk av punktet på grafen. Legg en linjal i flukt med grafen, slik at den kun tangerer grafen i det avmerkede punktet ( vanskelig å få nøyaktig dersom figuren er liten).Tegn den rette linjen og finn stogningstallet.

Derivasjon ved bruk av definisjonen

Vi har funksjonen

\[f(x) = x^2-2x+1 \]

og definisjonen

\[f'(x) = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

Vi setter funksjonen inn i definisjonen:

\[f'(x) = \lim_{\Delta x\to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

\[f'(x) = \lim_{\Delta x\to 0} \frac{(x+\Delta x)^2 - 2(x + \Delta x) +1 - (x^2-2x + 1)}{\Delta x} \]

\[f'(x) = \lim_{\Delta x\to 0} \frac{x^2+2x\Delta x + (\Delta x)^2 - 2x - 2\Delta x + 1 - x^2 +2x - 1}{\Delta x} \]

\[f'(x) = \lim_{\Delta x\to 0} \frac{2x\Delta x + ( \Delta x)^2 - 2\Delta x}{\Delta x} \]

\[f'(x) = \lim_{\Delta x\to 0} \frac{ \Delta x(2x +\Delta x-2)}{\Delta x} \]

\[f'(x) = \lim_{\Delta x\to 0} 2x + \Delta x - 2 \]

\[f'(x) = 2x - 2 \]

Nå slipper vi vanligvis å bruke definisjonen når vi deriverer, fordi vi har et sett med derivasjonsregler som gjør det lettere.

Derivasjonsregler

Polynomfunksjoner

Den deriverte av en konstant er null. Vi deriverer ledd for ledd. En potens med grunntall x deriveres slik: \[ f(x) = x^n, \quad \quad f'(x) = nx^{n-1}\]

\[ f(x) = kx^n, \quad \quad f'(x) = nkx^{n-1}\]

\[ f(x) = g(x) + h(x) + ..., \quad \quad f'(x) = g'(x) + h'(x) + ....\]

Eksempel:

\[ f(x) = x^4- 3x^2 + 3x - 1 \]

\[ f'(x) = 4x^3- 6x + 3 \]

I det første leddet trekkes fire ned foran x og eksponenten reduseres med en. I det andre leddet multipliseres 2 med faktoren som allerede står foran x. I ledd nr tre deriverer vi x og får 1, altså blir det 3 ganger 1 som er 3. Det siste leddet er -1, det er en konstant og den deriverte er da null.

Funksjoner med kvadratrot og n'te røtter

Funksjoner som inneholder

\[ \sqrt{x} \quad eller \quad \sqrt[m]{x^n} \] skrives om til \[ x^{\frac 12} \quad eller \quad x^{\frac nm} \]

Derivasjons regelen for potenser med x som grunntall (over) Gjelder

\[ f(x) =\sqrt{x}, \quad \quad \quad \quad f'(x)= (\sqrt{x})' = ( x^{\frac 12})' = \frac12 x^{- \frac 12} = \frac{1}{2 \sqrt{x}} \]

\[ f(x) =\sqrt[m]{x^n}, \quad \quad \quad \quad f'(x)= (\sqrt[m]{x^n})' = ( x^{\frac nm} )' = \frac nm x^{ \frac nm - 1} \]

Eksempel

\[ g(x) = 4 \sqrt{x} - \sqrt[6]{x^{5}} \]

\[ g'(x) = 4 \cdot \frac{1}{2 \sqrt{x}} - \frac 56 x^{ \frac 56 - 1} \]

Da er derivasjonen gjort, så er det å rydde opp litt:

\[ g'(x) = \frac{4}{2 \sqrt{x}} - \frac 56 x^{ -\frac 16} = \frac{2}{ \sqrt{x}} - \frac{5}{6 \sqrt[6]{x}} \]

Logaritme- og eksponential funksjoner

\[ f(x)= \ln|x|, \quad \quad \quad f'(x) = \frac 1x \]

\[ g(x)= e^x, \quad \quad \quad g'(x) = e^x \]

\[ h(x) = a^x \quad \quad \quad h'(x) = a^x \cdot ln a \]

Trigonometriske funksjoner

\[ f(x) = \sin(x), \quad \quad \quad f'(x) = \cos(x) \]

\[ f(x) = \cos(x), \quad \quad \quad f'(x) = -\sin(x) \]

\[ f(x) = \tan(x), \quad \quad \quad f'(x)=\frac{1}{cos^2x} \quad eller \quad f ' (x)= 1 + tan^2x \]

Til nå har vi sett hvordan enkle funksjoner har sine deriverte, men vi trenger noen metoder for sammensatte funksjoner som brøkfunksjoner, produkt av funksjoner, og funksjoner inne i en funksjon:

Produktregelen

\[ f(x) = g(x) \cdot h(x), \quad \quad \quad f'(x) = g'(x) \cdot h(x) + g(x) \cdot h'(x) \]

Eksempel:

\[ f(x) = x^4 \ln|x| \]

\[ f'(x) = 4x^3 \cdot \ln|x| + x^4 \cdot \frac 1x = x^3( 4 \ln|x| + 1) \]

Brøkfunksjoner

\[ f (x)=\frac{g(x)}{h(x)}, \quad \quad \quad f ' (x)= \frac{g'(x)\cdot h(x)- g(x)\cdot h'(x)}{(h(x))^2} \]

Kjerneregelen

\[ f(x) = g(u(x)), \quad \quad \quad f'(x) = g'(u) \cdot u'(x) \]

Eksempel

\[ f(x) = (x^2- \sqrt{x})^3 \] Setter $ u = x^2- \sqrt{x} $ og får \[ f'(x) = 3u^2 \cdot (2x - \frac{1}{2 \sqrt{x}} \]

TYPE	FUNKSJON	DERIVERT	EKSEMPEL
Produkt Bevis Eksempel Se video [1]	f(x)<math>\cdot</math>g(x)	[f(x)<math>\cdot</math>g(x)]'= f '(x)<math>\cdot</math>g(x)+ f(x)<math>\cdot</math>g '(x)	<math>(4x^3cos(x))'= 12x^2cos(x)-4x^3sin(x) \\ = 4x^2(3cos(x)-xsin(x))</math>
Kvotient	f (x)=<math>\frac{g(x)}{h(x)}</math> Bevis	f ' (x)=<math>\frac{g ' (x)\cdot h(x)- g(x)\cdot h ' (x)}{(h(x))^2}</math>	<math>( \frac{sin x}{2x^3})' \\ = \frac{cosx \cdot 2x^3 - 6x^2sinx}{4x^6}\\ = \frac{xcosx-3sinx}{2x^4}</math>
Kjerneregel	y = g(u) u er en funksjon av x	y ' = g ' (u)∙u'	<math>(sin(x^2))' = 2x cos(x^2)</math>

Grensekostnader

En kostnadsfunksjon uttrykker hva det koster å produsere x enheter av en vare.

Grensekostnaden forteller hvor mye kostnaden øker dersom man øker produksjonen fra x enheter til x+1 enheter.

Grensekostnaden er tilnærmet lik den deriverte av kostnadsfunksjonen

Eks. 1: Kostnaden ved produksjon av en vare er gitt som:

$K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]$

Der x er antall enheter.

Den deriverte av K(x) er:

K’(x) = 0,004x + 30

Man produseres 500 enheter og ønsker å finne økningen i kostnader når produksjonen økes til 501 enheter: K’(500) = 0,004 · 500 + 30 = 32

Det vil koste ca. 32 kroner å øke produksjonen fra 500 til 501 enheter.

Kostnaden ved å produsere henholdsvis 500 og 501 enheter er:

K(500) = 0,002 · 500 2 + 30 · 500 + 30 = 15.530kr.

K(501) = 0,002 · 501 2 + 30 · 501 + 30 = 15.562,002kr.

Man ser at nøyaktigheten ved å bruke den deriverte er god. Nøyaktigheten er størst når grafen krummer lite.

Kostnadsfunksjonen er en matematisk modell og vil trolig ikke gi det helt riktige bildet a virkeligheten. Derfor kan man bruke K’(x) når man skal finne grensekostnaden. Feilen er liten og regningen enklere.

Grenseinntekter

Dersom inntekten ved salg av et produkt er I(x) der x er solgte enheter er grenseinntekten I’(x). Grenseinntekten forteller hvor mye inntektene øker når salget øker fra x til x+1 enheter.

Overskudd

En virksomhets overskudd er inntekter minus kostnader.

O(x) = I(x) – K(x)

Overskuddet er størst når O’(x) = 0,

vi får:

O’(x) = I’(x) – K’(x)

O’(x) = 0

I’(x) – K’(x) = 0

I’(x) = K’(x)

Når grensekostnadene er lik grenseinntektene er overskuddet størst.

Eks. 2:

En bedrift har muligheten til å produsere 3000 enheter av et produkt. Hvor mange enheter må produseres for å maksimalisere overskuddet?

x [ 0, 3000]

Kostnadsfunksjonen er gitt som: $K(x) = 0,002x^2 + 30x +2000 $

$K’(x) = 0,004x + 30 $

Inntektsfunksjonen er gitt som: $I(x) = 0,0001x^2 + 40x$

$I’(x) = 0,0002x + 40 $

$K’(x) = I’(x)$

$0,004x + 30 = 0,0002x + 40$

$x = 2632$

Bedriften får størst overskudd ved å produsere 2632 enheter.

Maksimums og minimums problemer

Derivasjon er et egnet verktøy når man arbeider med maksimering eller minimering fordi den deriverte til funksjonen er null i et maksimumspunktet og minimumspunktet til funksjonen.

f’(x) = 0

gir deg alltid x verdien i et maksimums eller minimumspunkt, dersom de finnes.

Eks. 1

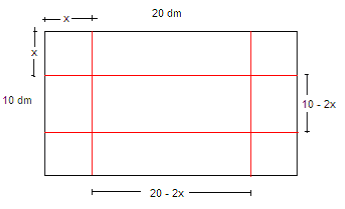
Du har en aluminiumsplate på en ganger to meter og ønsker å forme den til en boks med størst mulig volum.

Volumet av boksen er:

V(x) = bhl = x(20-2x)(10-2x) = x(200 – 40x – 20x +4x 2) = 4x 3 – 60x 2 +200x

V’(x) = 12x 2 – 120x +200

Setter den deriverte lik null:

V’(x) = 0

12x 2 – 120x + 200 = 0

x = 2,1 (tolkning av svarene fører til at vi forkaster den andre muligheten)

Det betyr at boksen får et størst volum dersom den har en høyde på 21 cm.

Eks. 2

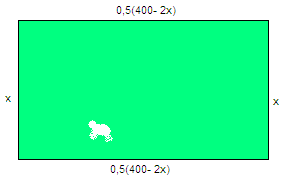
En bonde har en sau og 400 meter gjerde. Hun lurer på hvordan hun kan få det største arealet for sauen, ved å lage en innhegning som er firkantet.

Løsning:

Areal:

A(x) = x(200 – x) = 200x – x 2

Den deriverte av arealet:

A’(x) = 200 – 2x

Setter A’(x) = 0 og får

x = 100

Altså er det et kvadrat som gir størst areal.

Strekning, fart og akslerasjon

Et legeme tilbakelegger strekningen s i løpet av tiden t gitt ved s(t)

Legemets fart v er gitt som $v(t) = s'(t)$

Farten er den deriverte av strekningen.

Legemets akslerasjon a er gitt som

$a(t) = v'(t) = s¨(t)$

Akslerasjonen er den deriverte av farten, dvs. den dobbelderiverte av strekningen.

Eks. 3:

En partikkel forflytter seg etter $s(t) = 3,7t^2 $

Hvor langt forflytter partikkelen seg på 6 sekunder?' $s(6) = 3,7 · 6^2 = 133,2m $

Hva er partikkelen fart etter 4 sekunder?

$v(t) = s'(t) = 7,4t $

$v(4) = s'(4) =7,4 · 4 =29,6 m/s $

Hvor lang tid tar det før partikkelen beveger seg med 100 m/s? v(t) = 100 m/s gir

100m/s = 7,4t,

t =100/7,4 = ca. 13,5s

Hva er partikkelens akslerasjon? Er akslerasjonen konstant, eller varierer den med tiden?

$a(t) = v'(t) = 7,4m/s^2$ Man observerer at t ikke inngår i uttrykket for akslerasjonen, hvilket betyr at den er konstant 7,4 m/s 2, gjennom hele tidsforløpet.

---