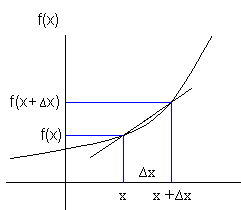Derivasjon
Definisjon
Den deriverte av en funksjon beskriver hastigheten funksjonene forandrer seg med, med hensyn på en uavhengig variabel. Den deriverte er også stigningen til tangenten av kurven. La oss anta at vi har funksjonen f(x) i et koordinatsystem. Vi velger et punkt x på førsteaksen. Tilhørende funksjonsverdi er f(x). La oss tenke oss at vi beveger oss et lite stykke bortover på førsteaksen fra x. Denne avstanden kaller vi ∆x. Dette nye punktet på førsteaksen heter da x+∆x. Funksjonsverdien til dette punktet blir f(x+∆x). Dette kan se slik ut:
Om vi så tenker oss at størrelsen på ∆x går mot null har vi følgende:
<math>f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} </math>
Den deriverte av f(x) skrives f '(x) og er gitt ved uttrykket over. Vi se at stigningstallet til sekanten vil nærme seg stigningstallet til grafens tangent i x, når ∆x går mot null.
Derivasjonsregler
Nedenfor følger en oversikt over de vanligste derivasjonsreglene for funksjoner med en variabel.
| TYPE | FUNKSJON | DERIVERT | EKSEMPEL |
| Potenser |
f(x) = xn | f '(x) = nxn-1 | <math>(x^3)' = 3x^2</math> |
| Konstant multiplisert med funksjon |
c f(x) | [c f(x)]' = c f '(x) | <math>(4x^3)' = 4 \cdot 3x^2 = 12x^2</math> |
| Konstant | f(x)= C | C' = 0 | (5)' = 0 |
| Polynom | f(x) = g(x)+ h(x) +... | f '(x) = g'(x) + h'(x) +... | <math>(x^3 -4x^2 +2x -1)' = 3x^2 - 8x + 2</math> |
| Eksponentialfunksjonen ax | f (x) = ax | f '(x) = axln a | |
| Eksponentialfunksjonen ex | f (x) = ex | f '(x) = ex | |
| Produkt Bevis Eksempel Se video [1] |
f(x)<math>\cdot</math>g(x) | [f(x)<math>\cdot</math>g(x)]'= f '(x)<math>\cdot</math>g(x)+ f(x)<math>\cdot</math>g '(x) | <math>(4x^3cos(x))'= 12x^2cos(x)-4x^3sin(x) \\ = 4x^2(3cos(x)-xsin(x))</math> |
| Sinus | f(x) = sin x | f'(x) = cos x | |
| Cosinus | f(x) = cos x | f'(x) = -sin x | |
| Tangens | f (x) = tan x | <math>f ' (x)=\frac{1}{cos^2x}</math> eller <math> f ' (x)= 1 + tan^2x </math> | |
| Kvotient | f (x)=<math>\frac{g(x)}{h(x)}</math> Bevis | f ' (x)=<math>\frac{g ' (x)\cdot h(x)- g(x)\cdot h ' (x)}{(h(x))^2}</math> | <math>( \frac{sin x}{2x^3})' \\ = \frac{cosx \cdot 2x^3 - 6x^2sinx}{4x^6}\\ = \frac{xcosx-3sinx}{2x^4}</math> |
| Kjerneregel | y = g(u) u er en funksjon av x |
y ' = g ' (u)∙u' | <math>(sin(x^2))' = 2x cos(x^2)</math> |
| Logaritme funksjonen | f(x) = ln |x| | f ' (x)=<math>\frac{1}{x}</math> | |
| Kvadratrot | f(x)=<math>\sqrt{x}</math> | f ' (x)=<math>\frac{1}{2\sqrt{x}}</math> | |
| Nte'rot | f(x)=<math>\sqrt[m]{x^n}=x^{\frac{n}{m}}</math> | Se potensfunksjon |
Grensekostnader
En kostnadsfunksjon uttrykker hva det koster å produsere x enheter av en vare.
Grensekostnaden forteller hvor mye kostnaden øker dersom man øker produksjonen fra x enheter til x+1 enheter.
Grensekostnaden er tilnærmet lik den deriverte av kostnadsfunksjonen
Eks. 1: Kostnaden ved produksjon av en vare er gitt som:
$K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]$
Der x er antall enheter. Den deriverte av K(x) er K’(x) = 0,004x + 30 Man produseres 500 enheter og ønsker å finne økningen i kostnader når produksjonen økes til 501 enheter: K’(500) = 0,004 · 500 + 30 = 32
Det vil koste ca. 32 kroner å øke produksjonen fra 500 til 501 enheter.
Kostnaden ved å produsere henholdsvis 500 og 5001 enheter er:
K(500) = 0,002 · 500 2 + 30 · 500 + 30 = 15.530kr.
K(501) = 0,002 · 501 2 + 30 · 501 + 30 = 15.562,002kr.
Man ser at nøyaktigheten ved å bruke den deriverte er god. Nøyaktigheten er størst når grafen krummer lite.
Kostnadsfunksjonen er en matematisk modell og vil trolig ikke gi det helt riktige bildet a virkeligheten. Derfor kan man bruke K’(x) når man skal finne grensekostnaden. Feilen er liten og regningen enklere.
Grenseinntekter
Dersom inntekten ved salg av et produkt er I(x) der x er solgte enheter er grenseinntekten I’(x). Grenseinntekten forteller hvor mye inntektene øker når salget øker fra x til x+1 enheter.
Overskudd
En virksomhets overskudd er inntekter minus kostnader.
O(x) = I(x) – K(x)
Overskuddet er størst når O’(x) = 0,
vi får:
O’(x) = I’(x) – K’(x)
O’(x) = 0
I’(x) – K’(x) = 0
I’(x) = K’(x)
Når grensekostnadene er lik grenseinntektene er overskuddet størst.
Eks. 2:
En bedrift har muligheten til å produsere 3000 enheter av et produkt. Hvor mange enheter må produseres for å maksimalisere overskuddet?
x [ 0, 3000]
Kostnadsfunksjonen er gitt som: K(x) = 0,002x2 + 30x +2000
K’(x) = 0,004x + 30
Inntektsfunksjonen er gitt som: I(x) = 0,0001x 2 + 40x
I’(x) = 0,0002x + 40
K’(x) = I’(x)
0,004x + 30 = 0,0002x + 40
x = 2632
Bedriften får størst overskudd ved å produsere 2632 enheter.
Maksimums og minimums problemer
Derivasjon er et egnet verktøy når man arbeider med maksimering eller minimering fordi den deriverte til funksjonen er null i et maksimumspunktet og minimumspunktet til funksjonen.
f’(x) = 0
gir deg alltid x verdien i et maksimums eller minimumspunkt, dersom de finnes.
Eks. 1
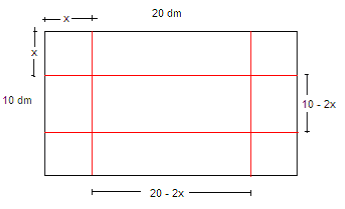
Du har en aluminiumsplate på en ganger to meter og ønsker å forme den til en boks med størst mulig volum.
Volumet av boksen er:
V(x) = bhl = x(20-2x)(10-2x) = x(200 – 40x – 20x +4x 2) = 4x 3 – 60x 2 +200x
V’(x) = 12x 2 – 120x +200
Setter den deriverte lik null:
V’(x) = 0
12x 2 – 120x + 200 = 0
x = 2,1 (tolkning av svarene fører til at vi forkaster den andre muligheten)
Det betyr at boksen får et størst volum dersom den har en høyde på 21 cm.
Eks. 2
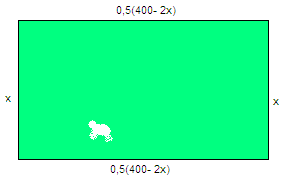
En bonde har en sau og 400 meter gjerde. Hun lurer på hvordan hun kan få det største arealet for sauen, ved å lage en innhegning som er firkantet.
Løsning:
Areal:
A(x) = x(200 – x) = 200x – x 2
Den deriverte av arealet:
A’(x) = 200 – 2x
Setter A’(x) = 0 og får
x = 100
Altså er det et kvadrat som gir størst areal.
Strekning, fart og akslerasjon
Et legeme tilbakelegger strekningen s i løpet av tiden t gitt ved s(t)
Legemets fart v er gitt som v(t) = s'(t)
Farten er den deriverte av strekningen.
Legemets akslerasjon a er gitt som a(t) = v'(t) = s(t)
Akslerasjonen er den deriverte av farten, dvs. den dobbelderiverte av strekningen.
Eks. 3:
En partikkel forflytter seg etter s(t) = 3,7t2
Hvor langt forflytter partikkelen seg på 6 sekunder?' s(6) = 3,7 · 62 = 133,2m
Hva er partikkelen fart etter 4 sekunder?
v(t) = s'(t) = 7,4t
v(4) = s'(4) =7,4 · 4 =29,6 m/s
Hvor lang tid tar det før partikkelen beveger seg med 100 m/s?
v(t) = 100 m/s gir 100m/s = 7,4t, t =100/7,4 = ca. 13,5s
Hva er partikkelens akslerasjon? Er akslerasjonen konstant, eller varierer den med tiden?
a(t) = v'(t) = 7,4m/s 2
Man observerer at t ikke inngår i uttrykket for akslerasjonen, hvilket betyr at den er konstant 7,4 m/s 2, gjennom hele tidsforløpet.