Modellering

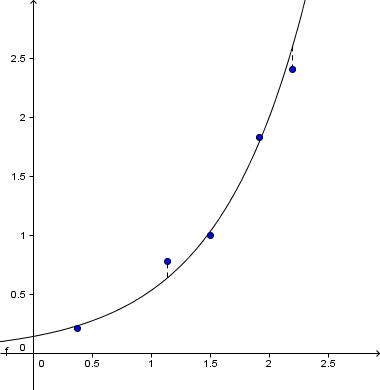
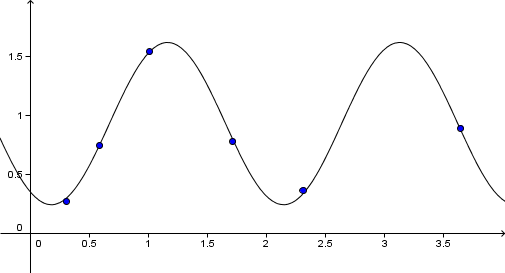
Modellering er en del av statistisk analyse der man fra en mengde målepunkter prøver å finne en matematisk sammenheng mellom variabler (parametre) og målinger.

Når man lager modeller har man i mange tilfeller bruk for et grafisk hjelpemiddel som kan gjøre grovarbeidet. Til dette brukes vanligvis grafiske kalkulatorer på skolen. Et gratis alternativ er Geogebra.

Statistisk modellering har anvendelser i mange praktiske fag, som fysikk, kjemi, økonomi og ingeniørfag.

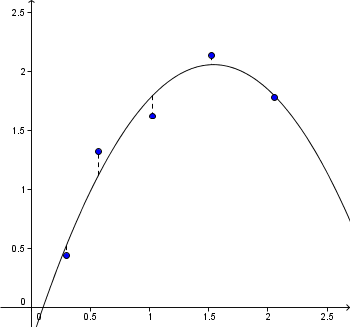
Hovedfokuset i fagene i videregående skole er å fra målepunktene kunne virdere hvilken type funksjon som best vil beskrive sammenhengen mellom parametre og målinger.

Teknikker for modellering

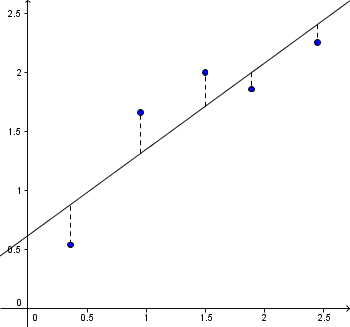
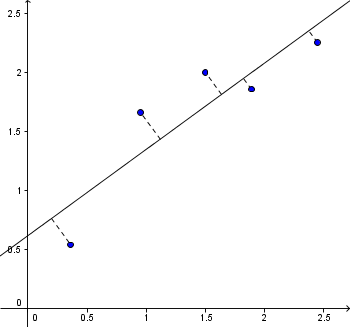
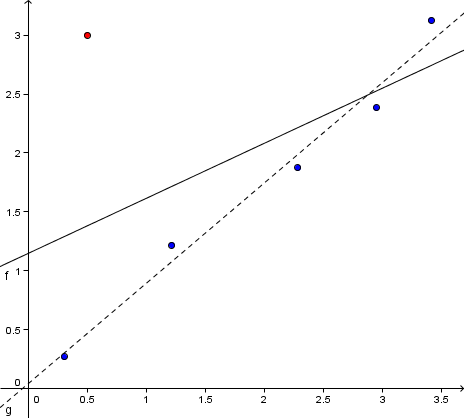
Algoritmene som brukes i tilpasningen av kuver til datapunkter er ofte så lange og omfattende at kun datamaskiner brukes. Det er likevel lurt å være klar over kriteriene som brukes for å bedømme om en gitt kurve er en god tilpasning, og hvilken kurve blandt flere som best beskriver den.

Korrelasjonskoeffesienten

Korrelasjonskoeffesienten er en statistisk størrelse som brukes for å måle korrespondansen mellom parametre og målinger. Den avhenger kun av datapunktene, ikke av kurvene, og er derfor ikke egnet til å bedømme om kurver er gode tilpasninger. Til det brukes metoden med minste kvadratsum.

Minste kvadraters avvik

Avvikende målepunkter

Lineær modellering

Ikke-lineær modellering

Polynomisk modellering

Eksponentiell modellering

Sinusoidal modellering