Modellering
Modellering er en del av statistisk analyse der man fra en mengde målepunkter prøver å finne en matematisk sammenheng mellom variabler (parametre) og målinger.
Når man lager modeller har man i mange tilfeller bruk for et grafisk hjelpemiddel som kan gjøre grovarbeidet. Til dette brukes vanligvis grafiske kalkulatorer på skolen. Et gratis alternativ er Geogebra.
Statistisk modellering har anvendelser i mange praktiske fag, som fysikk, kjemi, økonomi og ingeniørfag.
Hovedfokuset i fagene i videregående skole er å fra målepunktene kunne virdere hvilken type funksjon som best vil beskrive sammenhengen mellom parametre og målinger.
Teknikker for modellering
Algoritmene som brukes i tilpasningen av kuver til datapunkter er ofte så lange og omfattende at kun datamaskiner brukes. Det er likevel lurt å være klar over kriteriene som brukes for å bedømme om en gitt kurve er en god tilpasning, og hvilken kurve blandt flere som best beskriver den.
Korrelasjonskoeffesienten
Korrelasjonskoeffesienten er en statistisk størrelse som brukes for å måle korrespondansen mellom parametre og målinger. Den avhenger kun av datapunktene, ikke av kurvene, og er derfor ikke egnet til å bedømme om kurver er gode tilpasninger. Til det brukes metoden med minste kvadratavvik.
Minste kvadratavvik
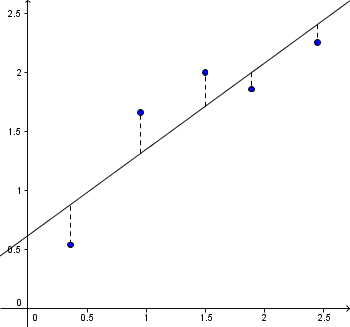
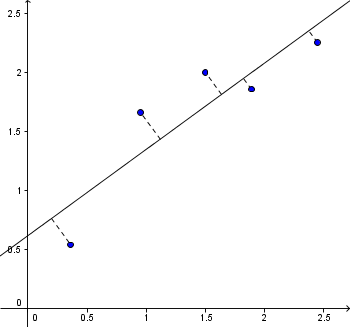
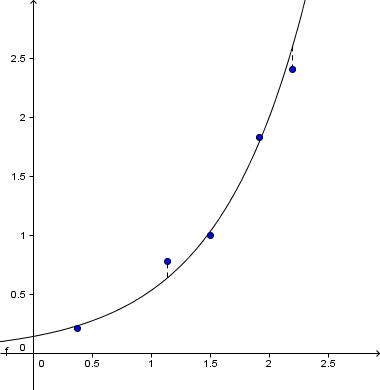
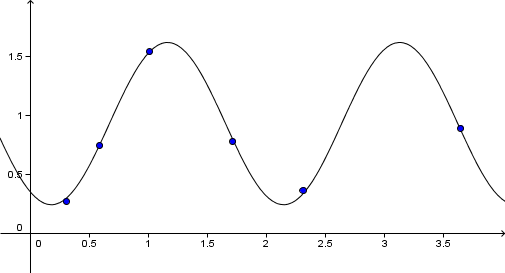
Minste kvadratavvik er den mest brukte metoden for tilpasning av kurver. Det finnes to måter å gjøre dette på; vertikalt avvik (venstre figur over) og vinkelrett avvik (høyre figur over). På grunn av de kompliserte algoritmene som må tas i bruk på sistnevnte, er det minste kvadratavvik med vertikalt avvik som er mest brukt.
Denne består av at man har en mengde målepunkter på formen <math>P_i(x_i,y_i)</math>, og at man fnner funksjonen <math>y=f(x)</math> slik at
<math>\sum_{i} \left( f(x_i)-y_i \right) ^2</math>
, der stor sigma står for sum over <math>i</math>, minimeres.
- Vertikalt kvadratavvik i Geogebra
- I den nyeste versjonen av Geogebra (Se lenke øverst på siden) er det mulig å beregne det kvadratavviket mellom en funksjon og en mengde målepunkter. Dette gjøres i følgende steg:
- 1. Lag en liste med punkter. Begynn med å legge målepunktene i grafikkfeltet. Dette kan du gjøre ved å bruke punkt-verktøyet, med regnearket eller ved å skrive
- i kommandolinjen for å lage et punkt med x-koordinat a og y-koordinat b. Legg så punktene i en liste (dersom du la ut punktene med regnearket har du allerede listen under navnet liste1 e.l.). For eksempel om du har målepunktene A-F skriver du
L={A,B,C,D,E,F}
- i kommandolinjen.
- 2. Lag funksjonen enten ved å skrive inn et funksjonsuttrykk i kommandolinjen eller ved å utføre en regresjon med målepunktene. Regresjon på målepunkter viser vi lenger nede i artikkelen.
- 3. Nå som du har en liste L med målepunkter og en funksjon f(x), kan vi finne kvadratavviket ved å skrive i kommandolinjen:
- Nå vil Geogebra holde styr på kvadratavviket selv om du flytter på målepunktene eller endrer funksjonsuttrykk på funksjonen.
Avvikende målepunkter
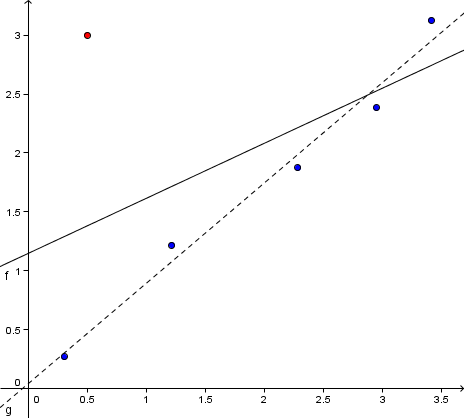
En del av modelleringsprosessen består av å vurdere målepunktene. Hvis det viser seg å finnes et målepunkt som ikke følger mønsteret til resten av målepunktene, kan det, avhengig av hva slags målinger du har, hende at du har en feilmåling. Ettersom vi bruker metoden med minste kvadratavvik vil et slikt punkt trekke mye på kurven og, om det er en feilmåling, ødelegge modellen. Et eksempel på et slikt punkt er markert med rødt i figuren over. Den heltrukne linjen viser en lineær regresjon der alle målepunktene er tatt i betraktning. Den stiplede linjen viser en lineær regresjon gjort med alle punktene untatt det røde avviket.
Lineær modellering
I lineær modellering prøver man å finne den beste funksjonen på formen <math>y=f(x)=ax+b</math> fra datapunktene. Det er den enkleste regresjonen og en som faktisk kan utføres for hånd om man ikke har en kalkulator.
- Lineær regresjon i Geogebra
- Her skal vi vise hvordan man gjør lineære regresjoner i Geogebra. Dette forklares punktvis som følger:
- 1. Lag en liste med punkter. Begynn med å legge målepunktene i grafikkfeltet. Dette kan du gjøre ved å bruke punkt-verktøyet, med regnearket eller ved å skrive
- i kommandolinjen for å lage et punkt med x-koordinat a og y-koordinat b. Legg så punktene i en liste (dersom du la ut punktene med regnearket har du allerede listen under navnet liste1 e.l.). For eksempel om du har målepunktene A-F skriver du
L={A,B,C,D,E,F}
- i kommandolinjen.
- 2. For å gjøre den lineære regresjonen bruker vi RegPoly-funksjonen dersom du bruker den norske versjonen av Geogebra. Skriv
- i kommandolinjen for å gjøre regresjonen.
- Lineær regresjon på Texas grafisk kalkulator
- Texaskalkulatorer er i stend til å utføre en rekke typer regresjon. Her skal vi stegvis forklare hvordan lineær regresjon utføres.
- 1. Først må du lage en liste med punkter. Du får fram listeredigeringsvinduet ved å gå trykke
- Deretter legger du inn x-verdiene til målepunktene i én liste, og de korresponderende y-verdiene (i riktig rekkefølge) i en annen. I denne forklaringer går vi ut ifra at x-erdiene er i L1-listen og y-verdiene er i L2-listen.
- 2. Nå bruker vi Linreg funksjonen for å utføre regresjonen:
- Trykk på knappene:
- Vi vil bruke listene vi la punktene inn i, her L1 og L2. Listene legger du til ved å trykke
- For liste 1 osv.
- Vi vil legge inn den tilpassede funksjonen i funksjonslisten. I denne forklaringen bruker vi Y1. Funksjonslisten finner du ved å trykke knappene
- Trykk ENTER-knappen for å starte regresjonen.
- Hvis alt har gått bra vil du få tilbake
- Linreg
- y=a+bx
- a=...
- b=...
- Og funksjonen Y1 , om du velget den, vil ha blitt skrevet om til funksjonen vist over.
- Du kan også plotte datapunktene dine i grafen slik at du kan vurdere tilpassningen med STAT PLOT-funksjonen.
Ikke-lineær modellering
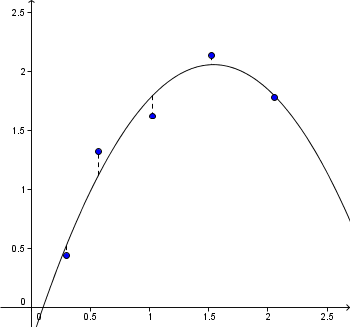
Polynomisk modellering
Eksponentiell modellering
Sinusoidal modellering