1T 2010 høst LØSNING
Løsning fra NDLA Løsning fra Nebu
DEL 1
Oppgave 1
a)
b)
1)
2)
c)
d)
<math> \frac{3}{x+4} + \frac{24}{x^2-16} = \frac{3}{x+4} + \frac{24}{(x+4)(x-4)}= \frac{3 (x-4)}{(x+4)(x-4)} + \frac{24}{(x+4)(x-4)}= \ \frac{3x-12}{(x+4)(x-4)} + \frac{24}{(x+4)(x-4)}= \frac{3x + 12}{(x+4)(x-4)} = \frac{3(x+4)}{(x+4)(x-4)}= \frac{3}{x-4}
</math>
e)
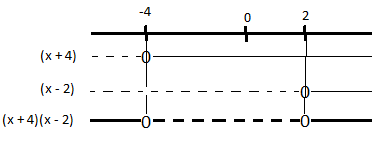
Bruker abc formelen og faktoriserer:
Tegner fortegnsskjema:
f)
g)
1)Sannsynlighet for å like begge:
2) Sannsynligheten for bare å like en:
Oppgave 2
a)
b)
Den gjennomsnittlige veksten fra x = 0 til x = 3 er null. Siden den momentane vekstfarten for x = 1 er -1 har funksjonen et minimumspunkt i intervallet.
c)
Sjekker forttegnet for den deriverte for x = -1 og x = 3 og finner at begge er positive. Fra før vet vi at den deriverte er negativ for x=1.
Maksimumspunkt:
Minimumspunkt:
DEL 2
Oppgave 3
a)
b)
Det vil finne sted når brøkeksponenten er en, altså etter 5730 år.
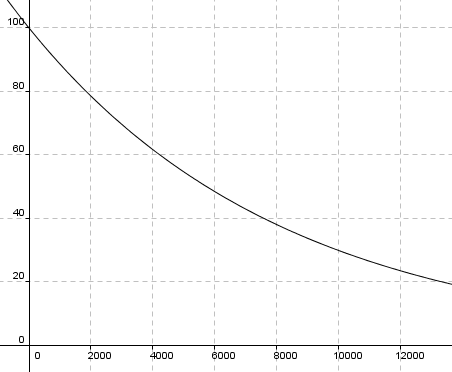
c)
<math>T(x) = 100 \cdot 0,5^{\frac{x}{5730}} \ \Downarrow \ 0,865 = 0,5^{\frac{x}{5730}} \ \Downarrow \ x = 5730 \cdot \frac{lg 0,865}{lg 0,5} = 1200
</math>
Brønnen var ca. 1200 år gammel.
Oppgave 4
a)
<math> tan(51,3^{\circ}) = \frac{h}{10m}\ \Downarrow \
x= 10 \cdot tan(51,3^{\circ})\ \Downarrow \ x = 12,48 m</math>
b)
c)
Finner først en vinkel ved å bruke cosinussetningen. Bruker så arealsetningen.
Dette er vinkelen mellom sidene som er 24m og 20m. Arealet blir:
Oppgave 5
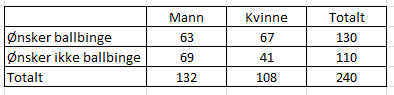
a)
b)
c)
d)
Det må verves 200 personer som ønsker ballbinge.
Oppgave 6
a)
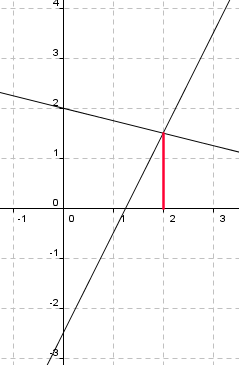
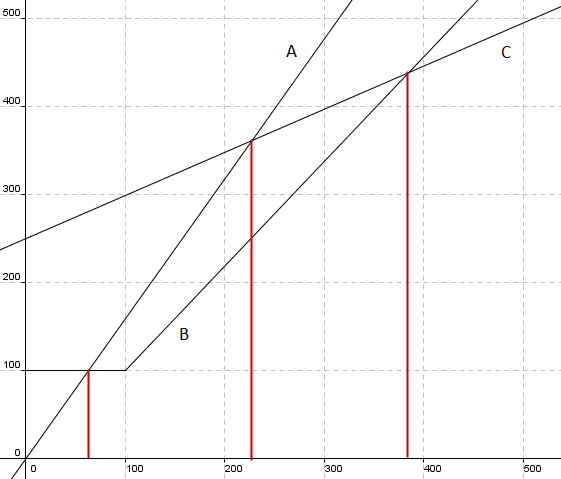
Den faste månedsprisen er ca. 90 kroner, lest av graf.
Pris for 500 minutter er 340kr. Prisen per ringeminutt blir da:
b)
c)
Dersom man ringer mindre enn 63 min. per måned er A billigst.
Dersom man ringer mellom 63 min. og 384 min. er B billigst.
Over 384 min. er C billigst
Oppgave 7
a)
Sannsynlighet for at alle er på Facebook: P(alle er på) =
Det er 27,8% sannsynlighet for at alle er på.
b)
Det er 99,2% sannsynlig at mer enn 20 har profil på Facebook.
Oppgave 8
Alternativ 1
a)
Toppunkt
b)
c)
Ser at funksjonen har konstantledd lik 4. Det betyr at grafen alltid går gjennom punktet (0,4) uansett x og a verdier. Den laveste verdi for toppunktet blir derfor når x = 0. Altså når det er symmetri om y aksen
dersom man bruker glider på a i Geogebra løser man både b og c ved inspeksjon.
Alternativ 2
a)
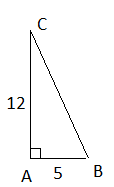
Bruker pytagoras: Desom trekanten er rettvinklet må siden på 27cm være hypotenusen.
må da være lik summen av kvadratene utspendt av eventuele kateter:
Hvilket betyr at trekanten IKKE er rettvinklet.
b)
Kaller det ukjente katetet for x og hypotenusen for y.
c)
Motstående side til vinkelen på 120 grader kaller vi y. Den ukjente tilstøtende siden til vinkelen på 120 grader blir da 4-y. Cosinussetningen gir:
Dvs: x = 1,2m og y = 2,8m