Radian: Forskjell mellom sideversjoner
Fra Matematikk.net
m Link |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
En radian er et vinkelmål der en hel omdreining rundt en sirkel er 2π radianer (to multiplisert med tallet pi). Det er derfor 360° per 2π radianer. Sammenhengen mellom grader og radianer er derfor: | En radian er et vinkelmål der en hel omdreining rundt en sirkel er 2π radianer (to multiplisert med tallet pi). Det er derfor 360° per 2π radianer. Sammenhengen mellom grader og radianer er derfor: | ||
[[ Bilde:Sirkelsegment.gif|right]] | [[ Bilde:Sirkelsegment.gif|right]] | ||
<tex>radianer | <tex>\text{radianer } = \text{ grader} \cdot \frac{\pi}{180} </tex> | ||
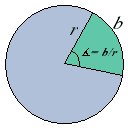
Buelengden b til et sirkelsegment med radius r utgjør b/(2πr) deler av omkretsen til sirkelen. Vinkelen, i radianer, til et sirkelsegment er derfor gitt ved b/r - se figuren. | Buelengden b til et sirkelsegment med radius r utgjør b/(2πr) deler av omkretsen til sirkelen. Vinkelen, i radianer, til et sirkelsegment er derfor gitt ved b/r - se figuren. | ||
Sideversjonen fra 7. jan. 2012 kl. 10:50
En radian er et vinkelmål der en hel omdreining rundt en sirkel er 2π radianer (to multiplisert med tallet pi). Det er derfor 360° per 2π radianer. Sammenhengen mellom grader og radianer er derfor:
<tex>\text{radianer } = \text{ grader} \cdot \frac{\pi}{180} </tex>
Buelengden b til et sirkelsegment med radius r utgjør b/(2πr) deler av omkretsen til sirkelen. Vinkelen, i radianer, til et sirkelsegment er derfor gitt ved b/r - se figuren.