Andregadslikninger og noen av tredje grad

Innledning

Fra siden om potenser uten brøkeksponent vet vi at $x \cdot x = x^2$. Sagt med ord sier vi at "$x$ multiplisert med seg selv er lik $x$ i andre". Andregradslikninger inneholder alltid et ledd hvor $x^2$ er en faktor.

En andregradslikning er en likning på formen $ax^2 + bx + c = 0$, der $a$, $b$ og $c$ er konstanter og $a \neq 0$. Konstantene i en annengradslikning kalles koeffisienter.

En løsninger av en likning kalles også en rot i likningen. Å finne røttene i en likning er altså det samme som å løse likningen.

En fullstendig andregradslikning skrives på formen

$ \displaystyle ax^2 + bx + c = 0 $

Likningen har tre ledd:

• <math> ax^2 </math> kalles andregradsleddet,
• <math> bx </math> kalles førstegradsleddet,
• <math> c </math> kalles konstantleddet.

Ufullstendig likninger

Dersom minst en av koeffisientene $b$ eller $c$ er lik null sier vi at andregradslikningen er ufullstendig. Dette er spesialtilfeller av andregradslikninger, fordi én av koeffisientene er lik null, slik at likningene mangler et ledd.

Dersom $a = 0$ har vi en førstegradslikning som løses med metoden beskrevet i likninger av første grad.

Tilfellet b = 0

Dersom $b = 0$ ser likningen slik ut:

$ \displaystyle ax^2 + c = 0 $

Denne løses med "bytt og flytt", for så å ta kvadratrot:

$ \begin{aligned} x = \pm \sqrt {- \frac {c}{a}} \end{aligned} $

Legg merke til at enten $a$ eller $c$ (men ikke begge!) må være negativ for at denne likningen skal ha en løsning. Vi kan ikke ta kvadratroten av et negativt tall.

Eksempel 1:

Løs likningen

$ \displaystyle 4x^2 - 8 = 0 $

Vi løser ved "bytt og flytt" og deretter ta kvadratroten:

$ \begin{aligned} 4x^2 &= 8 \\ x^2 &= \frac84 \\ x &= \pm \sqrt { \frac {8}{4}} \end{aligned} $

$ \displaystyle x = \sqrt {2} \qquad \vee \qquad x = - \sqrt {2} $

Tilfellet c = 0

Dersom $c = 0$ har vi følgende formel:

$ \displaystyle ax^2 + bx = 0 $

Vi løser ved faktorisering:

$ \displaystyle x (ax + b) = 0 $

$ \begin{aligned} x = 0 \qquad &\vee \qquad ax + b = 0 \\ x = 0 \qquad &\vee \qquad x = - \frac ba \end{aligned} $

Eksempel 2:

Løs likningen

$ \displaystyle -3x^2 + 6x = 0 $

Løsning ved faktorisering:

$ \displaystyle x (-3x + 6) = 0 $

$ \begin{aligned} x = 0 \qquad &\vee \qquad -3x + 6 = 0 \\ x = 0 \qquad &\vee \qquad x = 2 \end{aligned} $

ABC-formelen

En andregradslikning på formen $ax^2 + bx + c =0$ kan alltid løses ved hjelp av ABC-formelen, som ser slik ut:

ABC-formelen er

$ \displaystyle x= \frac{-b \pm \sqrt{b^2-4ac}}{2a} $

når

$ \displaystyle ax^2 + bx + c =0 $

• Dersom $b^2-4ac$ er positiv, vil likningen ha to ulike løsninger.
• Dersom $b^2-4ac = 0$ kan vi si at likningen har en enkelt løsning - eller også to like løsninger.
• Dersom $b^2 - 4ac$ er mindre enn null, får vi ingen løsning.

<b>Video eksempel:</b> Løser 2. gradslikning med abc formelen

Eksempel 3:

Løs likningen

$ \displaystyle 3x^2 + 2x - 1 =0 $

Likningen har koeffisenter $a = 3$ , $b = 2$ og $c = -1.$

Ved å bruke ABC-formelen får man:

$ \begin{aligned} x &= \frac{-2 \pm \sqrt{2^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3} \\ \\ &= \frac{-2 \pm \sqrt{4+12}}{6} \\ \\ &= \frac{-2 \pm 4}{6} \end{aligned} $

Likningen har to ulike løsninger:

$ \begin{aligned} x = \frac{-2 + 4}{6} \qquad &\vee \qquad x= \frac{-2 - 4}{6} \\ \\ x = \frac{1}{3} \qquad &\vee \qquad x = - 1 \end{aligned} $

Eksempel 4:

Finn røttene i likningen

$ \displaystyle -x^2 + 4x - 4 =0 $

Koeffisientene er $a = -1$ , $b = 4$ og $c = -4.$

Ved å bruke ABC-formelen får man:

$ \begin{aligned} x &= \frac{-4 \pm \sqrt{4^2-4 \cdot (-1) \cdot (-4)}}{2 \cdot (-1)} \\ \\ &= \frac{-4 \pm \sqrt{16-16}}{-2} \end{aligned} $

Med null under rottegnet får man kun en løsning, $x = 2$.

Eksempel 5:

Løs likningen:

<math>

\displaystyle 3x^2 + 2x + 2 =0 </math>

Koeffisientene er $a = 1$ , $b = -2$ og $c = 2$.

Ved å bruke ABC-formelen får man:

<math>

\begin{aligned} x &= \frac{2 \pm \sqrt{(-2)^2-4 \cdot 1 \cdot 2}}{2 \cdot 1} \\ \\ &= \frac{2 \pm \sqrt{4-8}}{2} \\ \\ &= \frac{2 \pm \sqrt{-4}}{2} \end{aligned} </math>

Her ser man et man får et negativt tall under rottegnet. Da er det på tide å stoppe opp og konkludere med at likningen ikke har reell løsning.

Eksempel 6:

Løs likningen:

<math>

\displaystyle 4x^2 - 1 =0 </math>

Koeffisientene er $a = 4$ , $b = 0$ og $c = -1.$

Likningen mangler førstegradsleddet ($b = 0$), og det enkleste i dette eksempelet er å bruke "bytt og flytt" og så ta kvadratroten, som vist over. Det er også fullt mulig å bruke ABC-formelen, og da får man:

<math>

\begin{aligned} x &= \frac{ \pm \sqrt{-4 \cdot 4 \cdot (-1)}}{2 \cdot 4} \\ \\ &= \frac{ \pm \sqrt{16}}{8} \\ \\ &=\pm \frac{ 4}{8} \end{aligned} </math>

Likningen har to løsninger:

<math>

\displaystyle x= \frac{1}{2} \qquad \vee \qquad x= - \frac{1}{2} </math>

Eksempel 7:

Løs likningen:

<math>

\displaystyle -3x^2 + 6x = 0 </math>

Koeffisentene er $a = -3$ , $b = 6$ og $c = 0.$

Ved å bruke ABC-formelen får man:

<math>

\begin{aligned} x &= \frac{-6 \pm \sqrt{6^2}}{-6} \\ \\ &= \frac{-6 \pm 6}{-6} \end{aligned} </math>

<math>

\displaystyle x= 2 \qquad \vee \qquad x= 0 </math>

Man ser at ABC-formelen virker her også, men siden konstantleddet mangler ($c = 0$), ville det være mer fornuftig å faktorisere ut $x$ og løse likningene som vist over.

<b>Video eksempel:</b> Løser 2. hvordan vet vi antall løsninger på en andregradslikning

Grafisk fremstilling av andregradslikninger

Hvorfor har noen likninger to løsninger, noen en og andre ingen? Det kan vi forstå dersom vi studerer grafen til andregradspolynomet i likningen. Løsninger i likningen finner vi som verdiene av $x$ der grafen skjærer $x$-aksen, det vil si der $y = 0$.

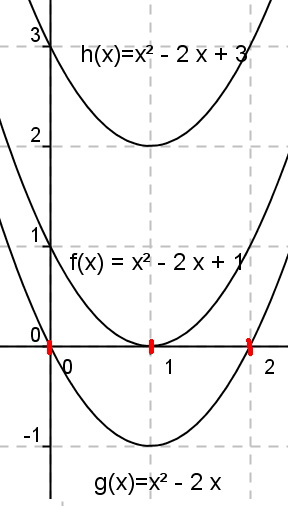
Figuren under viser tre ulike andregradspolynom.

Dersom grafen til andregradspolynomet krysser $x$-aksen, har likningen to løsninger. Likningen $g(x) = 0$ har to løsninger fordi $b^2-4ac>0$, og grafen til $g(x)$ skjærer $x$-aksen to steder.

Dersom grafen tangerer $x$-aksen har likningen en løsning. Likningen $f(x) = 0$ har en løsning fordi $b^2-4ac=0$. Grafen til $f(x)$ tangerer $x$-aksen i ett punkt, i $x= \frac{-b}{2a}$.

Dersom grafen til polynomet ikke krysser eller tangerer $x$-aksen, har likningen ingen løsning. Likningen $h(x) =0$ har ingen løsning fordi $b^2-4ac<0$. Man kan ikke ta kvadratroten av et negativt tall.

Bevis for ABC-formelen

For å bevise ABC-formelen bruker en første kvadratsetning, som vist i det følgende avsnittet.

$ \begin{aligned} ax^2 + bx + c &= 0 \\ \\ x^2 + \frac bax + \frac ca &= 0 \\ \\ x^2 + \frac bax &= - \frac ca \\ \\ x^2 + 2\frac {b}{2a}x &= - \frac ca \\ \\ x^2 + 2\frac {b}{2a}x + (\frac {b}{2a})^2 &= - \frac ca + (\frac {b}{2a})^2 \\ \\ (x +\frac {b}{2a})^2 &= - \frac ca + \frac {b^2}{4a^2} \\ \\ (x +\frac {b}{2a})^2 &= - \frac {4ac}{4a a} + \frac {b^2}{4a^2} \\ \\ (x +\frac {b}{2a})^2 &= \frac {-4ac+b^2}{4a^2} \\ \\ (x +\frac {b}{2a}) &= \pm \sqrt{\frac {b^2 -4ac}{4a^2}} \\ \\ x &= -\frac {b}{2a} \pm {\frac {\sqrt {b^2 -4ac}}{2a}} \\ \\ x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a} \end{aligned} $

Fullstendig kvadrat

Man kan bygge opp et fullstendig kvadrat ved å halvere, kvadrere, addere.....
For å kunne bruke teknikken må du kunne kvadratsetningene godt.

Det følgende eksempelet viser hvordan det gjøres:

Eksempel 8:

Løs likningen

$ \displaystyle 2x^2 - 3x +1 = 0 $

Vi omformer likningen:

$ \begin{aligned} x^2 - \frac 32 x + \frac 12 &=0 \\ \\ x^2 - \frac 32 x &= - \frac 12 \\ \\ x^2 - \frac 32 x &= - \frac 12 \\ \\ x^2 - \frac 32 x + ( \frac 34)^2 &= - \frac 12 + ( \frac 34)^2 \\ \\ (x - \frac 34)^2 &= \frac {1}{16} \end{aligned} $

$ \begin{aligned} x - \frac 34 = \sqrt{ \frac {1}{16}}\qquad &\vee \qquad x - \frac 34 = -\sqrt{ \frac {1}{16}} \\ \\ x = 1\qquad &\vee \qquad x = \frac {1}{2} \end{aligned} $

Dersom du sliter med algebra bør du kanskje holde deg til ABC-formelen, men dersom du har oversikt og har ambisjoner om god karakter (5,6), er metoden med fullstendig kvadrat noe du bør beherske.

Andregradslikninger på produktform

Man kan ha andregradslikninger på formen:

<math>

\displaystyle (x + 1)(x – 2) = 0 </math>

Du ser at dette er en andregradslikning om du multipliserer ut parentesene:

<math>

\displaystyle (x + 1)(x – 2) = x^2 - 2x + x – 2 = x^2 – x – 2 </math>

Man kan multiplisere ut faktorene som vist over og bruke ABC–formelen, men det finnes en mye enklere måte å løse likningen på:

Dersom produktet av to faktorer skal bli null, må en av faktorene være null.

Likningen $mn = 0$ medfører at $m$ eller $n$ må være lik null, om likningen skal være oppfylt.

I eksemplet

<math>

\displaystyle (x + 1)(x – 2) = 0 </math>

betyr det at $x+1 = 0$ , eller at $x – 2 = 0$.

Det gir løsningene $x = -1$ og $x = 2$.

Problemet er redusert til løsninger av to enkle førstegradslikninger.

Faktorisering av andregradsuttrykk

Det generelle andregradsuttrykket er $ax^2 + bx + c.$ Ofte har man behov for å faktorisere uttrykket for å kunne forkorte og forenkle.

Man har følgende formel for faktorisering av andregradsuttrykk:

$ \displaystyle ax^2 + bx + c = a( x-x_1)(x-x_2) $

Der $x_1$ og $x_2$ er løsninger av $ax^2 + bx + c = 0.$

Eksempel 9:

Faktoriser polynomet

$ \displaystyle 6x^2-4x-2 $

Vi løser først likningen $6x^2-4x-2=0$ ved hjelp av ABC-formelen og får

$ \displaystyle x_1 = 1 \qquad \vee \qquad x_2 = - \frac13 $

Så bruker vi formelen over og får:

$ \displaystyle 6x^2-4x-2 = a(x-x_1)(x-x_2) = 6(x-1)(x + \frac 13) $

Denne fremgangsmåten er spesielt nyttig (helt nødvendig) når man skal forkorte brøker som inneholder andregradspolynomer.

Eksempel 9:

Skriv enklest mulig:

<math>

\displaystyle \frac{6x^2-4x-2}{x + \frac13} </math>

Vi faktoriserer og får:

<math>

\displaystyle \frac{6(x-1)(x + \frac 13)}{x + \frac13} = 6(x-1) </math>

Sum og produkt av røtter

Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger):

En fullstendig andregradslikning skrives på formen

$ \displaystyle ax^2 + bx + c = 0 $

Dersom $x_1$ og $x_2$ er røtter (løsninger) i likningen, så er

$ \begin{aligned} x_1 + x_2 &= - \frac ba \\ \\ x_1 \cdot x_2 &= \frac ca \end{aligned} $

Eksempel 10:

Vi ønsker å finne et andregradsuttrykk som har røttene $x = -2$ og $x = 1$. Utover det har vi ingen andre krav.

Vi får:

<math>

\begin{aligned} x_1 + x_2 &=- \frac ba \\ \\ -2 + 1 &= - \frac ba \\ \\ a &= b \end{aligned} </math>

Siden vi ikke har krav til koeffisientene kan vi jo velge $a = 1$. Da får vi at $a = 1$ og $b = 1$.

Produktet av røttene må oppfylle likningen

<math>

\begin{aligned} x_1 \cdot x_2 &= \frac ca \\ \\ -2 \cdot 1 &= \frac ca \\ \\ c &= -2 \end{aligned} </math>

Vi får da likningen

<math>

\displaystyle x^2 + x - 2 = 0 </math>

Ved å bruke ABC-formelen ser man at dette er en (av mange) likninger som har løsning for $x = 1$ og for $x = -2.$

Dersom man anvender disse formlene og finner en likning, må man sjekke at den virkelig har løsninger.

---

Tilbake til 1T Hovedside

Hovedside