Andregradslikninger: Forskjell mellom sideversjoner
m Manglende mellomrom mellom ord |
|||
| (147 mellomliggende versjoner av 4 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
== Innledning == | |||
Fra siden om [[potenser uten brøkeksponent]] vet vi at | |||
Andregradslikninger inneholder alltid et ledd hvor | |||
<br> | |||
En '''andregradslikning''' er en likning på formen | |||
En løsninger av en likning kalles også en ''rot'' i likningen. Å finne røttene i en likning er altså det samme som å løse likningen. | |||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
En fullstendig andregradslikning skrives på formen | |||
= | :<math> | ||
\displaystyle | |||
ax^2 + bx + c = 0 | |||
</math> | |||
Likningen har tre ledd: | |||
< | * <math> ax^2 </math> kalles andregradsleddet, | ||
* | |||
* <math> c </math> kalles konstantleddet. | |||
</ | </div> | ||
<br> | |||
<br> | |||
== Ufullstendig likninger == | |||
Dersom minst en av koeffisientene | |||
Dette er spesialtilfeller av andregradslikninger, fordi én av koeffisientene er lik null, slik at likningene mangler et ledd. | |||
Dersom | |||
<br> | |||
=== Tilfellet b = 0 === | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
Dersom | Dersom $b = 0$ ser likningen slik ut:<br> | ||
:<math> | |||
\displaystyle | |||
ax^2 + c = 0 | |||
</math> | |||
Denne løses med "bytt og flytt", for så å ta kvadratrot: | |||
:<math> | |||
\begin{aligned} | |||
x = \pm \sqrt {- \frac {c}{a}} | |||
\end{aligned} | |||
</math> | |||
Legg merke til at enten | |||
</div> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' | |||
<br> | |||
Løs likningen | |||
:<math> | |||
\displaystyle | |||
4x^2 - 8 = 0 | |||
</math> | |||
Vi løser ved "bytt og flytt" og deretter ta kvadratroten: | |||
:<math> | |||
\begin{aligned} | |||
4x^2 &= 8 \ | |||
x^2 &= \frac84 \ | |||
x &= \pm \sqrt { \frac {8}{4}} | |||
\end{aligned} | |||
</math> | |||
:<math> | |||
\displaystyle | |||
x = \sqrt {2} \qquad \vee \qquad x = - \sqrt {2} | |||
</math> | |||
</div> | |||
<br> | |||
=== Tilfellet c = 0 === | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
<br> | |||
Dersom | |||
:<math> | |||
\displaystyle | |||
ax^2 + bx = 0 | |||
</math> | |||
Vi løser ved faktorisering: | |||
:<math> | |||
\displaystyle | |||
x (ax + b) = 0 | |||
</math> | |||
:<math> | |||
\begin{aligned} | |||
x = 0 \qquad &\vee \qquad ax + b = 0 \ | |||
x = 0 \qquad &\vee \qquad x = - \frac ba | |||
\end{aligned} | |||
</math> | |||
</div> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' | |||
<br> | |||
Løs likningen | |||
:<math> | |||
\displaystyle | |||
-3x^2 + 6x = 0 | |||
</math> | |||
Løsning ved faktorisering: | |||
:<math> | |||
\displaystyle | |||
x (-3x + 6) = 0 | |||
</math> | |||
:<math> | |||
\begin{aligned} | |||
x = 0 \qquad &\vee \qquad -3x + 6 = 0 \ | |||
x = 0 \qquad &\vee \qquad x = 2 | |||
\end{aligned} | |||
</math> | |||
</div> | |||
== ABC-formelen == | |||
En andregradslikning på formen | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
ABC-formelen er | |||
:<math> | |||
\displaystyle | |||
x= \frac{-b \pm \sqrt{b^2-4ac}}{2a} | |||
</math> | |||
når | |||
:<math> | |||
\displaystyle | |||
ax^2 + bx + c =0 | |||
</math> | |||
Dersom | |||
</div> | |||
<br> | |||
(I høyere kurs viser man at likningen kan ha [[komplekse løsninger]]).<br><br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 1:''' | |||
<br> | |||
Løs likningen | |||
:<math> | |||
\displaystyle | |||
3x^2 + 2x - 1 =0 | |||
</math> | |||
Likningen har koeffisenter $a = 3$ , | |||
Ved å bruke ABC-formelen får man: | |||
x( | :<math> | ||
\begin{aligned} | |||
x &= \frac{-2 \pm \sqrt{2^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3} \ \ | |||
&= \frac{-2 \pm \sqrt{4+12}}{6} \ \ | |||
&= \frac{-2 \pm 4}{6} | |||
\end{aligned} | |||
</math> | |||
Likningen har to ulike løsninger: | |||
:<math> | |||
\begin{aligned} | |||
x = \frac{-2 + 4}{6} \qquad &\vee \qquad x= \frac{-2 - 4}{6} \ \ | |||
x = \frac{1}{3} \qquad &\vee \qquad x = - 1 | |||
\end{aligned} | |||
</math> | |||
</div> | |||
<br> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"><br> | |||
'''Eksempel 2:''' | |||
<br> | |||
Finn røttene i likningen | |||
:<math> | |||
\displaystyle | |||
-x^2 + 4x - 4 =0 | |||
</math> | |||
Koeffisientene er $a = -1$ , $b = 4 | |||
<br> | |||
Ved å bruke ABC-formelen får man: | |||
:<math> | |||
\begin{aligned} | |||
x &= \frac{-4 \pm \sqrt{4^2-4 \cdot (-1) \cdot (-4)}}{2 \cdot (-1)} \ \ | |||
&= \frac{-4 \pm \sqrt{16-16}}{-2} | |||
\end{aligned} | |||
</math> | |||
Med null under rottegnet får man kun en løsning, | |||
</div> | |||
<br> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 3:''' | |||
<br> | |||
Løs likningen: | |||
:<math> | |||
\displaystyle | |||
3x^2 + 2x + 2 =0 | |||
</math> | |||
Koeffisientene er $a = 1$ , $b = -2$ og $c = 2$. | |||
<br> | |||
Ved å bruke ABC-formelen får man: | |||
:<math> | |||
\begin{aligned} | |||
x &= \frac{2 \pm \sqrt{(-2)^2-4 \cdot 1 \cdot 2}}{2 \cdot 1} \ \ | |||
&= \frac{2 \pm \sqrt{4-8}}{2} \ \ | |||
&= \frac{2 \pm \sqrt{-4}}{2} | |||
\end{aligned} | |||
</math> | |||
Her ser man et man får et negativt tall under rottegnet. Da er det på tide å stoppe opp og konkludere med at likningen ikke har reell løsning. | |||
</div> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 4:''' | |||
<br> | |||
Løs likningen: | |||
:<math> | |||
\displaystyle | |||
4x^2 - 1 =0 | |||
</math> | |||
Koeffisientene er | |||
<br> | |||
Likningen mangler førstegradsleddet ( | |||
Det er også fullt mulig å bruke ABC-formelen, og da får man: | |||
:<math> | |||
\begin{aligned} | |||
x &= \frac{ \pm \sqrt{-4 \cdot 4 \cdot (-1)}}{2 \cdot 4} \ \ | |||
&= \frac{ \pm \sqrt{16}}{8} \ \ | |||
&=\pm \frac{ 4}{8} | |||
\end{aligned} | |||
</math> | |||
Likningen har to løsninger: | |||
:<math> | |||
\displaystyle | |||
x= \frac{1}{2} \qquad \vee \qquad x= - \frac{1}{2} | |||
</math> | |||
</div> | |||
<br><br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 5:''' | |||
<br> | |||
Løs likningen: | |||
:<math> | |||
\displaystyle | |||
-3x^2 + 6x = 0 | |||
</math> | |||
Koeffisentene er | |||
<br> | |||
Ved å bruke ABC-formelen får man: | |||
:<math> | |||
\begin{aligned} | |||
x &= \frac{-6 \pm \sqrt{6^2}}{-6} \ \ | |||
&= \frac{-6 \pm 6}{-6} | |||
\end{aligned} | |||
</math> | |||
:<math> | |||
\displaystyle | |||
x= 2 \qquad \vee \qquad x= 0 | |||
</math> | |||
Man ser at ABC-formelen virker her også, men siden konstantleddet mangler ( | |||
</div> | |||
<br> | |||
<br> | |||
== Grafisk fremstilling av andregradslikninger == | |||
Hvorfor har noen likninger to løsninger, noen en og andre ingen? Det kan vi forstå dersom vi studerer grafen til andregradspolynomet i likningen. | |||
Løsninger i likningen finner vi som verdiene av | |||
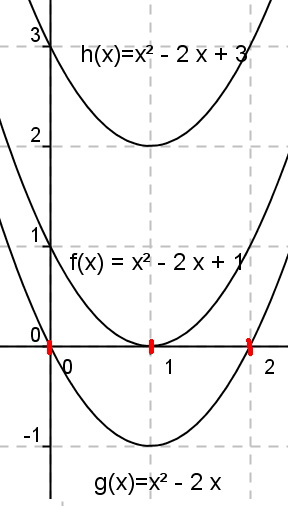
Figuren under viser tre ulike andregradspolynom. | |||
<br> | |||
[[Bilde:2likn.PNG]] | |||
<br><br> | |||
Dersom grafen til andregradspolynomet krysser | |||
Dersom grafen tangerer | |||
Dersom grafen til polynomet ikke krysser eller tangerer | |||
<br> | |||
<br> | |||
== Bevis for ABC-formelen == | |||
For å bevise ABC-formelen bruker en [[kvadratsetningene|første kvadratsetning]], som vist i det følgende avsnittet. | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
:<math> | |||
\begin{aligned} | |||
ax^2 + bx + c &= 0 \ \ | |||
x^2 + \frac bax + \frac ca &= 0 \ \ | |||
x^2 + \frac bax &= - \frac ca \ \ | |||
x^2 + 2\frac {b}{2a}x &= - \frac ca \ \ | |||
x^2 + 2\frac {b}{2a}x + (\frac {b}{2a})^2 &= - \frac ca + (\frac {b}{2a})^2 \ \ | |||
(x +\frac {b}{2a})^2 &= - \frac ca + \frac {b^2}{4a^2} \ \ | |||
(x +\frac {b}{2a})^2 &= - \frac {4ac}{4a a} + \frac {b^2}{4a^2} \ \ | |||
(x +\frac {b}{2a})^2 &= \frac {-4ac+b^2}{4a^2} \ \ | |||
(x +\frac {b}{2a}) &= \pm \sqrt{\frac {b^2 -4ac}{4a^2}} \ \ | |||
x &= -\frac {b}{2a} \pm {\frac {\sqrt {b^2 -4ac}}{2a}} \ \ | |||
x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a} | |||
\end{aligned} | |||
</math> | |||
</div> | |||
<br> | |||
<br> | |||
== Fullstendig kvadrat == | |||
Man kan bygge opp et fullstendig kvadrat ved å ''halvere, kvadrere, addere.....'' | |||
<br> | |||
For å kunne bruke teknikken må du kunne [[kvadratsetningene]] godt. | |||
<br> | |||
Det følgende eksempelet viser hvordan det gjøres: | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel: ''' | |||
<br> | |||
Løs likningen | |||
:<math> | |||
\displaystyle | |||
2x^2 - 3x +1 = 0 | |||
</math> | |||
Vi omformer likningen: | |||
:<math> | |||
\begin{aligned} | |||
x^2 - \frac 32 x + \frac 12 &=0 \ \ | |||
x^2 - \frac 32 x &= - \frac 12 \ \ | |||
x^2 - \frac 32 x &= - \frac 12 \ \ | |||
x^2 - \frac 32 x + ( \frac 34)^2 &= - \frac 12 + ( \frac 34)^2 \ \ | |||
(x - \frac 34)^2 &= \frac {1}{16} | |||
\end{aligned} | |||
</math> | |||
:<math> | |||
\begin{aligned} | |||
x - \frac 34 = \sqrt{ \frac {1}{16}}\qquad &\vee \qquad x - \frac 34 = -\sqrt{ \frac {1}{16}} \ \ | |||
x = 1\qquad &\vee \qquad x = \frac {1}{2} | |||
\end{aligned} | |||
</math> | |||
</div> | |||
<br> | |||
Dersom du sliter med algebra bør du kanskje holde deg til ABC-formelen, men dersom du har oversikt og har ambisjoner om god karakter (5,6), er metoden med fullstendig kvadrat noe du bør beherske. | |||
<br> | |||
<br> | |||
== Andregradslikninger på produktform == | |||
Man kan ha andregradslikninger på formen: | |||
:<math> | |||
\displaystyle | |||
(x + 1)(x – 2) = 0 | (x + 1)(x – 2) = 0 | ||
</math> | |||
Du ser at dette er en andregradslikning om du multipliserer ut parentesene: | |||
(x + 1)(x – 2) = | :<math> | ||
\displaystyle | |||
(x + 1)(x – 2) = x^2 - 2x + x – 2 = x^2 – x – 2 | |||
</math> | |||
Man kan multiplisere ut faktorene som vist over og bruke | Man kan multiplisere ut faktorene som vist over og bruke ABC–formelen, men det finnes en mye enklere måte å løse likningen på: | ||
Dersom produktet av to faktorer skal bli null, må en av faktorene være null. | Dersom produktet av to faktorer skal bli null, må en av faktorene være null. | ||
mn = 0 medfører at m eller n må være lik null, om | Likningen $mn = 0$ medfører at $m$ eller $n$ må være lik null, om likningen skal være oppfylt. | ||
I eksemplet | I eksemplet | ||
:<math> | |||
\displaystyle | |||
(x + 1)(x – 2) = 0 | (x + 1)(x – 2) = 0 | ||
</math> | |||
betyr det at x+1 = 0 , eller at x – 2 = 0 | betyr det at $x+1 = 0$ , eller at $x – 2 = 0$. | ||
Det gir løsningene x = -1 | Det gir løsningene $x = -1 | ||
Problemet er redusert til løsninger av to enkle | Problemet er redusert til løsninger av to enkle førstegradslikninger. | ||
<br> | |||
<br> | |||
== Faktorisering av andregradsuttrykk == | |||
Det generelle andregradsuttrykket er $ax^2 + bx + c.$ Ofte har man behov for å faktorisere uttrykket for å kunne forkorte og forenkle. | |||
Man har følgende formel for faktorisering av andregradsuttrykk: | Man har følgende formel for faktorisering av andregradsuttrykk: | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
:<math> | |||
\displaystyle | |||
ax^2 + bx + c = a( x-x_1)(x-x_2) | |||
</math> | |||
Der | |||
</div> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' | |||
<br> | |||
Faktoriser polynomet | |||
:<math> | |||
\displaystyle | |||
6x^2-4x-2 | |||
</math> | |||
Vi løser først likningen | |||
:<math> | |||
\displaystyle | |||
x_1 = 1 \qquad \vee \qquad x_2 = - \frac13 | |||
</math> | |||
Så bruker vi formelen over og får: | |||
:<math> | |||
\displaystyle | |||
6x^2-4x-2 = a(x-x_1)(x-x_2) = 6(x-1)(x + \frac 13) | |||
</math> | |||
Denne fremgangsmåten er spesielt nyttig (helt nødvendig) når man skal forkorte brøker som inneholder andregradspolynomer. | |||
</div> | |||
<br> | |||
Sum og produkt av røtter | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' | |||
<br> | |||
Skriv enklest mulig: | |||
:<math> | |||
\displaystyle | |||
\frac{6x^2-4x-2}{x + \frac13} | |||
</math> | |||
Vi faktoriserer og får: | |||
:<math> | |||
\displaystyle | |||
\frac{6(x-1)(x + \frac 13)}{x + \frac13} = 6(x-1) | |||
</math> | |||
</div> | |||
<br> | |||
<br> | |||
== Sum og produkt av røtter == | |||
Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger): | Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger): | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
En fullstendig andregradslikning skrives på formen | |||
:<math> | |||
\displaystyle | |||
ax^2 + bx + c = 0 | |||
</math> | |||
Dersom | |||
:<math> | |||
\begin{aligned} | |||
x_1 + x_2 &= - \frac ba \ \ | |||
x_1 \cdot x_2 &= \frac ca | |||
\end{aligned} | |||
</math> | |||
</div> | |||
<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel:''' | |||
<br> | |||
Vi ønsker å finne et andregradsuttrykk som har røttene | |||
<br><br> | |||
Vi får: | |||
:<math> | |||
\begin{aligned} | |||
x_1 + x_2 &=- \frac ba \ \ | |||
-2 + 1 &= - \frac ba \ \ | |||
a &= b | |||
\end{aligned} | |||
</math> | |||
Siden vi ikke har krav til koeffisientene kan vi jo velge | |||
<br> | |||
Produktet av røttene må oppfylle likningen | |||
:<math> | |||
\begin{aligned} | |||
x_1 \cdot x_2 &= \frac ca \ \ | |||
-2 \cdot 1 &= \frac ca \ \ | |||
c &= -2 | |||
\end{aligned} | |||
</math> | |||
Vi får da likningen | |||
:<math> | |||
\displaystyle | |||
x^2 + x - 2 = 0 | |||
</math> | |||
Ved å bruke ABC-formelen ser man at dette er en (av mange) likninger som har løsning for | |||
<br> | |||
Dersom man anvender disse formlene og finner en likning, må man sjekke at den virkelig har løsninger. | |||
</div> | |||
---- | |||
[[1T Hovedside|Tilbake til 1T Hovedside]]<p></p> | |||
[[Hovedside]] | |||
[[Category:Algebra]][[Category:Ped]][[Category:1T]] | |||
Siste sideversjon per 28. okt. 2019 kl. 10:52
Innledning
Fra siden om potenser uten brøkeksponent vet vi at
En andregradslikning er en likning på formen
En løsninger av en likning kalles også en rot i likningen. Å finne røttene i en likning er altså det samme som å løse likningen.
En fullstendig andregradslikning skrives på formen
- <math>
\displaystyle ax^2 + bx + c = 0 </math>
Likningen har tre ledd:
Ufullstendig likninger
Dersom minst en av koeffisientene
Dersom
Tilfellet b = 0
Dersom
- <math>
\displaystyle ax^2 + c = 0 </math>
Denne løses med "bytt og flytt", for så å ta kvadratrot:
- <math>
Legg merke til at enten
Eksempel:
Løs likningen
- <math>
\displaystyle 4x^2 - 8 = 0 </math>
Vi løser ved "bytt og flytt" og deretter ta kvadratroten:
- <math>
- <math>
\displaystyle x = \sqrt {2} \qquad \vee \qquad x = - \sqrt {2} </math>
Tilfellet c = 0
Dersom
- <math>
\displaystyle ax^2 + bx = 0 </math>
Vi løser ved faktorisering:
- <math>
\displaystyle x (ax + b) = 0 </math>
- <math>
Eksempel:
Løs likningen
- <math>
\displaystyle -3x^2 + 6x = 0 </math>
Løsning ved faktorisering:
- <math>
\displaystyle x (-3x + 6) = 0 </math>
- <math>
ABC-formelen
En andregradslikning på formen
ABC-formelen er
- <math>
\displaystyle x= \frac{-b \pm \sqrt{b^2-4ac}}{2a} </math>
når
- <math>
\displaystyle ax^2 + bx + c =0 </math>
Dersom
Eksempel 1:
Løs likningen
- <math>
\displaystyle 3x^2 + 2x - 1 =0 </math>
Likningen har koeffisenter
Ved å bruke ABC-formelen får man:
- <math>
Likningen har to ulike løsninger:
- <math>
Eksempel 2:
Finn røttene i likningen
- <math>
\displaystyle -x^2 + 4x - 4 =0 </math>
Koeffisientene er
Ved å bruke ABC-formelen får man:
- <math>
Med null under rottegnet får man kun en løsning,
Eksempel 3:
Løs likningen:
- <math>
\displaystyle 3x^2 + 2x + 2 =0 </math>
Koeffisientene er
Ved å bruke ABC-formelen får man:
- <math>
Her ser man et man får et negativt tall under rottegnet. Da er det på tide å stoppe opp og konkludere med at likningen ikke har reell løsning.
Eksempel 4:
Løs likningen:
- <math>
\displaystyle 4x^2 - 1 =0 </math>
Koeffisientene er
Likningen mangler førstegradsleddet (
- <math>
Likningen har to løsninger:
- <math>
\displaystyle x= \frac{1}{2} \qquad \vee \qquad x= - \frac{1}{2} </math>
Eksempel 5:
Løs likningen:
- <math>
\displaystyle -3x^2 + 6x = 0 </math>
Koeffisentene er
Ved å bruke ABC-formelen får man:
- <math>
- <math>
\displaystyle x= 2 \qquad \vee \qquad x= 0 </math>
Man ser at ABC-formelen virker her også, men siden konstantleddet mangler (
Grafisk fremstilling av andregradslikninger
Hvorfor har noen likninger to løsninger, noen en og andre ingen? Det kan vi forstå dersom vi studerer grafen til andregradspolynomet i likningen.
Løsninger i likningen finner vi som verdiene av
Figuren under viser tre ulike andregradspolynom.
Dersom grafen til andregradspolynomet krysser
Dersom grafen tangerer
Dersom grafen til polynomet ikke krysser eller tangerer
Bevis for ABC-formelen
For å bevise ABC-formelen bruker en første kvadratsetning, som vist i det følgende avsnittet.
- <math>
Fullstendig kvadrat
Man kan bygge opp et fullstendig kvadrat ved å halvere, kvadrere, addere.....
For å kunne bruke teknikken må du kunne kvadratsetningene godt.
Det følgende eksempelet viser hvordan det gjøres:
Eksempel:
Løs likningen
- <math>
\displaystyle 2x^2 - 3x +1 = 0 </math>
Vi omformer likningen:
- <math>
- <math>
Dersom du sliter med algebra bør du kanskje holde deg til ABC-formelen, men dersom du har oversikt og har ambisjoner om god karakter (5,6), er metoden med fullstendig kvadrat noe du bør beherske.
Andregradslikninger på produktform
Man kan ha andregradslikninger på formen:
- <math>
\displaystyle (x + 1)(x – 2) = 0 </math>
Du ser at dette er en andregradslikning om du multipliserer ut parentesene:
- <math>
\displaystyle (x + 1)(x – 2) = x^2 - 2x + x – 2 = x^2 – x – 2 </math>
Man kan multiplisere ut faktorene som vist over og bruke ABC–formelen, men det finnes en mye enklere måte å løse likningen på:
Dersom produktet av to faktorer skal bli null, må en av faktorene være null.
Likningen
I eksemplet
- <math>
\displaystyle (x + 1)(x – 2) = 0 </math>
betyr det at
Det gir løsningene
Problemet er redusert til løsninger av to enkle førstegradslikninger.
Faktorisering av andregradsuttrykk
Det generelle andregradsuttrykket er
Man har følgende formel for faktorisering av andregradsuttrykk:
- <math>
\displaystyle ax^2 + bx + c = a( x-x_1)(x-x_2) </math>
Der
Eksempel:
Faktoriser polynomet
- <math>
\displaystyle 6x^2-4x-2 </math>
Vi løser først likningen
- <math>
\displaystyle x_1 = 1 \qquad \vee \qquad x_2 = - \frac13 </math>
Så bruker vi formelen over og får:
- <math>
\displaystyle 6x^2-4x-2 = a(x-x_1)(x-x_2) = 6(x-1)(x + \frac 13) </math>
Denne fremgangsmåten er spesielt nyttig (helt nødvendig) når man skal forkorte brøker som inneholder andregradspolynomer.
Eksempel:
Skriv enklest mulig:
- <math>
\displaystyle \frac{6x^2-4x-2}{x + \frac13} </math>
Vi faktoriserer og får:
- <math>
\displaystyle \frac{6(x-1)(x + \frac 13)}{x + \frac13} = 6(x-1) </math>
Sum og produkt av røtter
Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger):
En fullstendig andregradslikning skrives på formen
- <math>
\displaystyle ax^2 + bx + c = 0 </math>
Dersom
- <math>
Eksempel:
Vi ønsker å finne et andregradsuttrykk som har røttene
Vi får:
- <math>
Siden vi ikke har krav til koeffisientene kan vi jo velge
Produktet av røttene må oppfylle likningen
- <math>
Vi får da likningen
- <math>
\displaystyle x^2 + x - 2 = 0 </math>
Ved å bruke ABC-formelen ser man at dette er en (av mange) likninger som har løsning for
Dersom man anvender disse formlene og finner en likning, må man sjekke at den virkelig har løsninger.