Statistikkutkast

1. Utvalg

Dersom man produserer 1000 enheter av noe per dag og ønsker å sjekke kvaliteten kan det være for tidkrevende å sjekke alle 1000. Vi kan ta et tilfeldig utvalg, en stikkprøve, og ved å få informasjon om utvalget kan vi forhåpentligvis si litt om hele produksjonen. Desto større utvalget er desto mer representativt er det trolig for populasjonen, men man må jo foreta en avveining i forhold til hva som er praktisk mulig. Når man analyser tallmaterialet kan man selvsagt gjøre det for hånd, men det er tidkrevende og digitale hjelpemidler er gode på dette. Fordelen med å bruke regneark eller programmering er at du trolig vil treffe disse igjen etter vgs. Du kan også bruke Geogebra, men det er ikke sikkert du støter på dette programmet etter vgs.

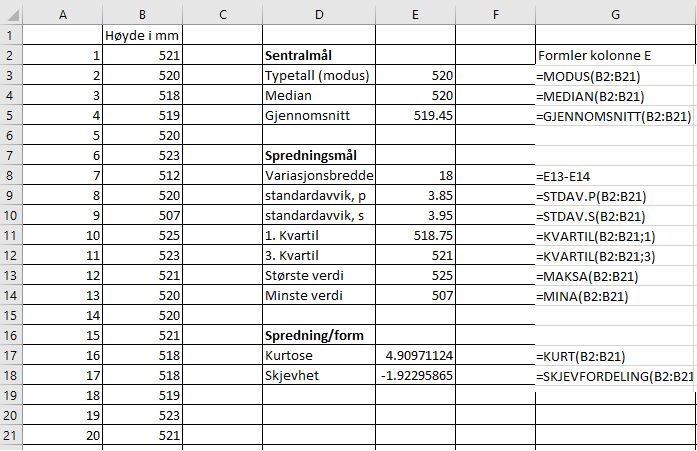
2. Statistikk komandoer i Excel

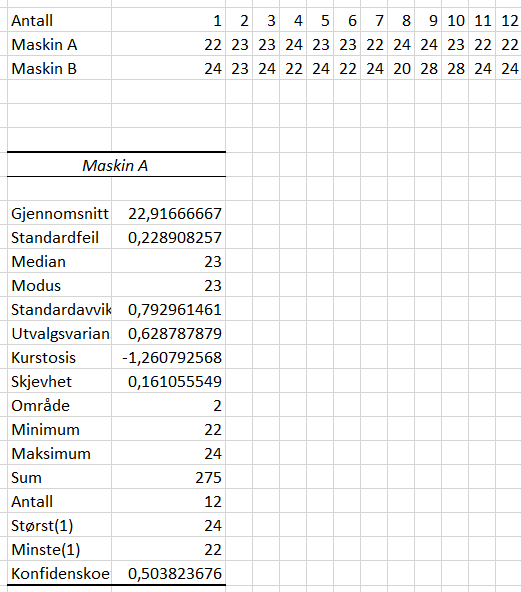
Figuren viser en del nyttige funksjoner i Excel Dersom du kun trenger en eller et par av størrelsene kan du bruke funksjonene vist i kolonne G. Dersom du har bruk for de leste kan det være praktisk å bruke DATAANALYSE - DESKRIPTIV STATISTIKK. Du vil da få noe lignende tabellen under.

3. Begreper i statistikk

Populasjon - det totale antall individer eller objekter et sted eller over en tidsperiode. Eks: Alle harene i Nordmarka. Alle epleneprodusert i Hardanger i 2023.

utvalg En del (liten) av populasjonen- Målet er å kunne si noe fornuftig / få kunnskap om populasjoner (store mengder) på grunnlag av små mengder - utvalg.

Stokastisk variabel

Estimator Gjennomsnittet av et utvalg $\bar{x}$ er en naturlig estimator for $\mu$, den ukjente forventningsverdien til hele populasjonen.

Kurtose. Normalfordelingen har kurtose 3. Høyere tall indikerer større forekomst av ekstreme verdier og motsatt.

Skjevhet. Dersom skjevheten er null er fordelingen symmetrisk. En fordeling kan ha positiv skjevhet, null ( symmetrisk) eller negativ. Dersom forskyvningen er null betyr det at medianverdi er sammenfallende med gjennomsnittsverdi. Gjennomsnitt > median er høyre forskyvning og er en positiv forskyvning. Median > gjennomsnitt gir en forskyvning mot venstre, en negativ forskyvning.

Det er mange måter og formler for å måle skjevhet (eng: Skewness) på, og Pearsons median skjevhet er blant de enkleste.

$ PearsMedS =3 \cdot \frac{gjennomsnitt - median}{standardavvik}$

Spredningsmål

4. Normalfordeling

Funksjonen har en klokkeformet graf:

$f(x)= \frac{1}{\sigma \sqrt{2 \pi}} e^{- \frac{(x-\mu)^2}{2 \sigma^2}}$

der $\mu$ er forventningsverdien og $\sigma$ er standardavviket.

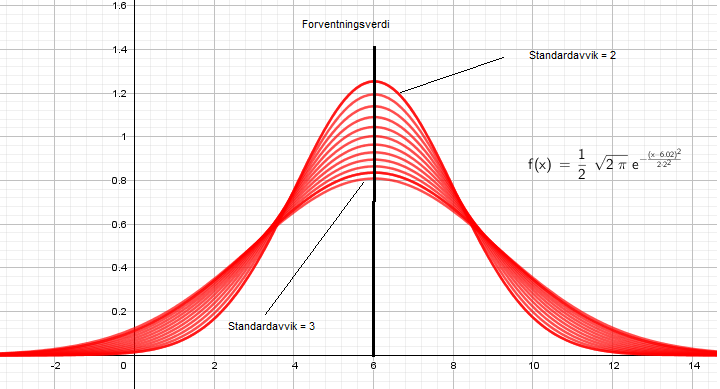
Figuren illustrere hvordan standardavviket påvirker klokkeformen. Grafene har standardavvik fra 3 til 2. Desto mindre standardavviket blir, desto raskere nærmer grafen seg x aksen, på begge sider av forventningsverdien.

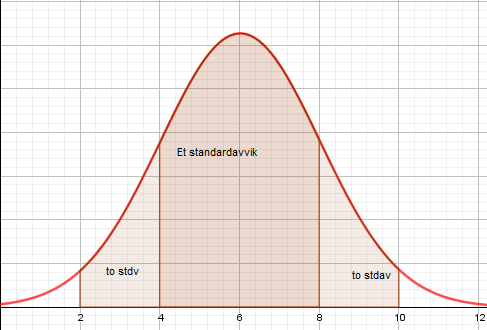
Figuren viser en normalfordeling med forventning 6 og standardavvik 2. Arealet under grafen fra x= 4 til x = 8 tilsvarer ett standardavvik og er ca 68% av forekomstene. To standardavvik er CA 95% og tre ca 100% ( ca 0,2% > 3 standardavvik).

Litt mer matematisk:

$P(\mu - \sigma \leq X \leq \mu + \sigma) = 0,683$

$P(\mu -2 \cdot \sigma \leq X \leq \mu + 2 \cdot \sigma) = 0,945$

$P(\mu - 3 \cdot \sigma \leq X \leq \mu + 3 \cdot \sigma) = 0,997$

5. Standardnormalfordelingen

En stokastisk variabel X med forventning $\mu =10 $ og standardavvik $\sigma = 3$ kan standardiseres ved variabelen Z.

$Z = \frac{X - \mu}{\sigma}$

Z er normalfordelt med forventning lik 0 og standardavvik 1. Z er standardnormalfordelt.

Eksempel:

I avsnittet om Excel kommandoer hadde utvalget på 20 enheter $\bar{x} = 519,45$. La oss anta at standardavviket for hele populasjonen er $ \sigma = 5,0$. (Normalt kjenner vi ikke populasjonens standardavvik, men vi kommer til det senere).

Standardavviket for utvalget blir da: $\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} = \frac{5}{\sqrt{20}} =1,1$

Dersom vi går to standardavvik hver vei fra $\bar{x}$ kan vi med 95% sannsynlighet si at forventningsverdien til populasjonen, $\mu$ ligger i det intervallet: [519,45 - 2,2 , 519,45 + 2,2] eller [517,25 , 521,65]

Dette er et 95% konfidensintervall for $\mu$

6. To stokastisk variable

To uavhengige stokastiske variable X og Y der X med forventning $\mu_x$ og standardavvik $\sigma_x$, og Y med forventning $\mu_Y$ og standardavvik $\sigma_Y$.

X-Y vil være normalfordelt med forventning $\mu_X - \mu_Y$ og standardavvik $ \sqrt{\sigma_x^2 + \sigma_Y^2}$

7. Konfidensintervall

Et intervall der vi tror en ukjent parameter ligger, kalles et konfidensintervall. Et konfidensintervall har et konfidensnivå som sier noe om hvor sannsynlig det er å finne den ukjente parameteren i intervallet. Det er vanlig å bruke et konfidensnivå på 95%, altså er det da 95% sannsynlig at parameteren man jakter på ligger i intervallet. Det er 5% sannsynlig at den ikke gjør det.

7.1. Konfidensintervall for $\mu$ når $\sigma$ er ukjent (T- intervall)

Vi kjøper to is, en fra maskin A og en fra maskin B. Hvor store er disse?

Når standardavviket er ukjent er standardfeilen ukjent. Vi bruker da $SE ( \bar x) = \frac{s}{\sqrt{n}}$

Vi bruker:

$T = \frac{\bar x - \mu}{\frac{s}{\sqrt{n}}}$

Det vil gi et såkalt T- intervall:

$[ \bar x - t_{\frac{\alpha}{2}} \cdot \frac{s}{\sqrt n}, \bar x + t_{\frac{\alpha}{2}} \cdot \frac{s}{\sqrt n}]$

I Excel :

8. Punktestimat for $\mu$

Vår beste gjetning på populasjonens forventningsverdi $\mu$ er gjennomsnittet av utvalget.

$\overline{X} = \frac 1n \displaystyle\sum_{i=1}^{n} X_i$

Gjennomsnittet av utvalget, $\overline{x}$ er i seg selv en stokastisk variabel da den er gjennomsnittet av tilfeldig utvalgte verdier. $\overline{X}$ har forventningsverdi $\mu$ og standardavvik $\frac{\sigma}{\sqrt{n}}$

Dersom vi har valget mellom flere estimatorer bruker vi den med minst varians.

9. Punktestimat for $\sigma$

Et estimat for variansen er $S^2 = \frac{1}{n-1}\displaystyle\sum_{i=1}^{n} (X_i - \overline{X})^2 $

Man har funnet at å dele på n-1 i stedet for n gjør at $S^2$ blir en god forventningsrettet estimator for $\sigma^2$ under generelle betingelser.

$S^2$ er forventningsrettet for $\sigma^2$, men $S$ er ikke forventningsrettet for $\sigma$, men brukes likevel da feilen i praksis er liten.

Siden vi normalt ikke kjenner standardavviket bruker vi $\frac {s}{\sqrt{n}}$ som kalles standardfeilen til gjennomsnittet.

10. t - fordelingen

Fra sentralgrenseteoremet vet vi at z er tilnærmet normalfordelt:

$Z = \frac{\overline{x}- \mu}{\frac{\sigma}{\sqrt{n}}}$

Vi kjenner sjelden populasjonenes standardavvik $ \sigma$, og må bruke s:

$t = \frac{\overline{x}- \mu}{\frac{S}{\sqrt{n}}}$

t har "feitere haler" enn normalfordelingen og lavere maksimumsverdi. Ved mer enn 30 observasjoner er fordelingene ganske like.

11. Hypotesetesting

En hypotese har alltid en motsatt hypotese, slik at man har to hypoteser. Dersom påstanden er "produkt A er bedre enn produkt B", så eksisterer også hypotesen om at A ikke er er bedre enn B.

Vi formulerer hypotesene $H_1$ og $H_0$. Bevisbyrden ligger på $H_1$ som utfordrer. Tvilen kommer nullhypotesen $H_0$ til gode.

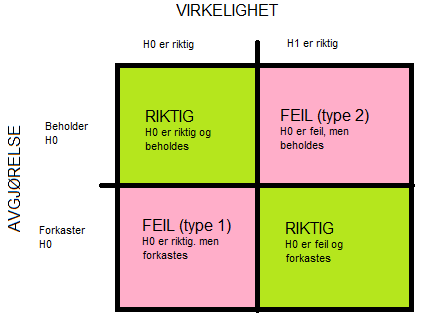
Vi må ta et valg og følgende fire alternativer er mulige:

Det er ikke gitt at utfallet blir riktig, men ved å følge trinnene nedenfor har man et godt utgangspunkt:

1 Formulere en modell og hypoteser

2 Vi finner en stokastisk variabel vi kan basere våre beslutninger på. En slik variabel kalles for testobservator, og vi må kjenne sannsynlighetsfordelingen til denne.

3 Hva tenker vi om feilmargin og signifikansnivå?

12. t -test

Når brukes T-test?

En t-test er en statistisk test som brukes til å sammenligne gjennomsnittet for to grupper. Det brukes ofte i hypotesetesting for å avgjøre om en prosess eller behandling faktisk har en effekt på populasjonen av interesse, eller om to grupper er forskjellige fra hverandre. T testen kan si noe om det er signifikante forskjeller i datamaterialet for gruppene. Dersom man vil kun vil undersøke om det er forskjell på gruppene uten å si noe om hvem som eventuelt er størst, bruker man en tosidig test. Dersom man har en mistanke om at elementene i en gruppe er større inn i den andre, kan man bruke en ensidig test.

Forutsetninger

Følgende antagelser gjør om dataene:

1. er uavhengige.

2. er (omtrent) normalfordelte.

3. ha tilnærmet lik varians innenfor hver gruppe som sammenlignes (varianshomogenitet).

4. Variablene må være metriske (tall).

Man bør ha 20-30 datapunkter, men testen er god med relativt få punkter. Har du mange (50+ )bruker du z testen.

Hypotesene

$H_0$	$H_A$	Forkaster $H_0$
$\mu \leq \mu_0$	$\mu > \mu_0$>	$T > t_{\alpha}$
$\mu \geq \mu_0$	$\mu < \mu_0$>	$T < - t_{\alpha}$
$\mu = \mu_0$	$\mu \neq \mu_0$>	$ |T| > t_{\frac{\alpha}{2}}$

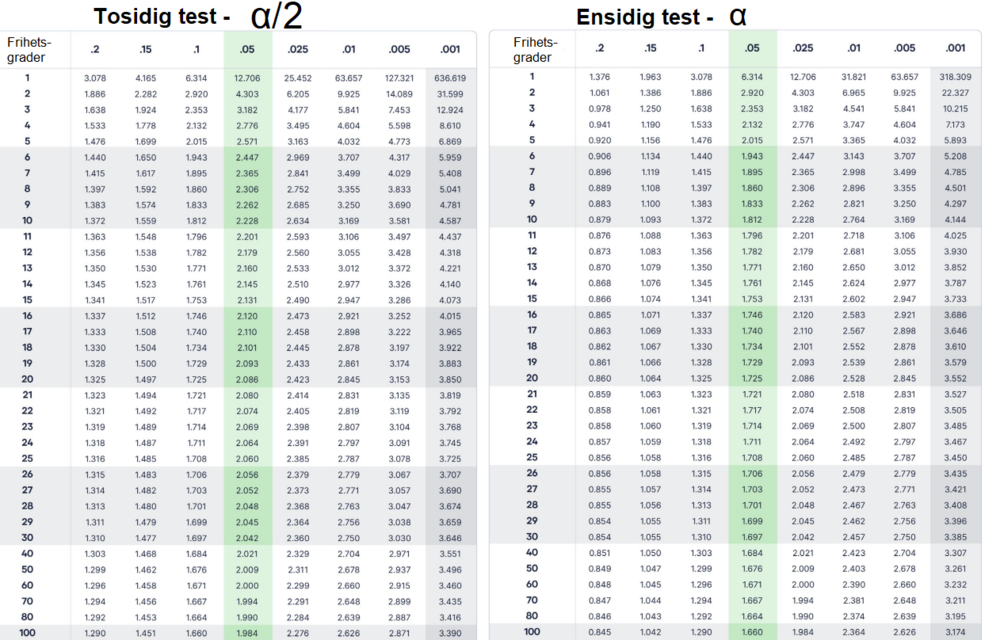
t - tabell

Tabellverdier er hentet fra: https://www.scribbr.com/statistics/students-t-table/. Frihetsgradene i kolonnen til venstre er antall observasjoner minus en. Sammenlignes to datasett er frihetsgradene summen av observasjoner i begge settene, minus to.

Det er tre typer T-tester

1 en-utvalgs t-test

Brukes dersom man studerer en gruppes gjennomsnitt ( $\overline{x}$ ) opp mot en kjent standard verdi / referanseverdi $\mu$

Nullhypotese, $H_0$: $\quad \overline{x} = \mu $

Alternativ hypotese, $H_A$ : $\quad \overline{x} \neq \mu $

Antall frihetsgrader er antall observasjoner minus en: fr = n - 1

Eks:

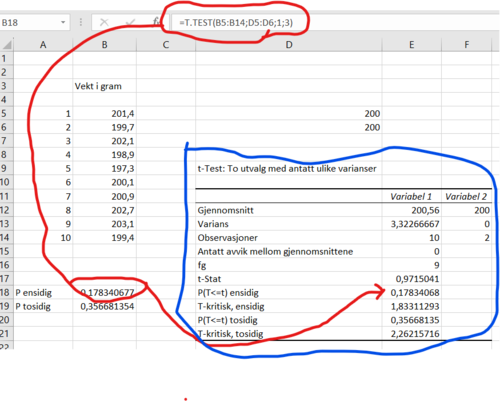
Et gatekjøkken påstår at de selger burgere som veier 200 gram. Gjør de virkelig det? Vi plukker ut 10 burgere tilfeldig, på forskjellige tidspunkt og kontrollveier:

201,4 199,7 202,1 198,9 197,3 200,1 200,9 202,7 203,1 199,4

Som nullhypotese er det naturlig å velge at burgeren veier 200 gram eller mer, altså en ensidig test.

$H_0: \overline x \geq 200$

$ H_1: \overline x < 200$

Manuell regning:

• Vi finner tesobservatoren T: $\quad T = \frac{\bar x - \mu}{\frac{s}{\sqrt{n}}}= \frac{200,56 - 200} {\frac{1,823}{\sqrt{10}}} = 0,9716$
• Vi har 9 frihetsgrader ( 10 observasjoner).

• Vi forkaster $H_0$ dersom $T < t_{0,05} = 1,833$

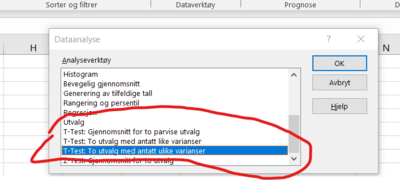
Løsning ved hjelp av Excel:

Velg DATA fra menyen øverst på skjermen. Helt til høyre finner du DATAANALYSE. Velg den.

Løsning ved hjelp av Geogebra:

Når forkaster vi nullhypotesen?

2. to-utvalgs t-test (uavhengig test)

Hvis gruppene kommer fra to forskjellige populasjoner (f.eks. to forskjellige arter, eller mennesker fra to separate byer) uavhengige av hverandre. Vi sammenligner gjennomsnittet i de to gruppene.

Nullhypotese $H_0 : µ_A - µ_B = 0$

Alternative hypotese: $H_A : µ_A - µ_B ≠ 0$

Frihetsgrader: $fr = n_A + n_B - 2$

Eks:

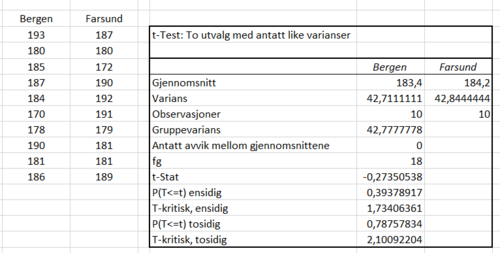
Er gutter på 19 åt fra Bergen høyere enn gutter på 19 år fra Farsund? Vi har ingen mistanker i noen retninger og vil derfor utføre en tosidig test. Vi måler 10 tilfeldige fra hvert sted og får følgende tabell:

Nullhypotese $H_0 : \mu_B - \mu_F = 0$ Det er ingen forskjell.

Alternative hypotese: $H_A : \mu_B - \mu_F ≠ 0$ Det er en signifikant forskjell.

Signifikansnivå $\alpha = 0,05$ = 5%

Forkaster $H_0$ dersom:

$T > t_{\alpha} \quad \quad \quad \quad P < \alpha$

$T> 2.101 \quad \quad P < 0,05 \quad \quad$ (2,101 fra tabell, 18 frihetsgrader)

Vi trenger:

Testobservator T, eller P verdi. På grunnlag av det kan man konkludere.

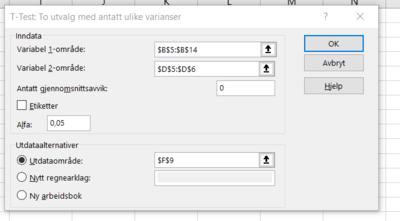
Løsning ved Excel

Vi observerer at både T og P støtter at vi beholder nullhypotesen. Vi kan altså si med 95% sikkerhet at det ikke er noen høydeforskjell på 19 åringer i Bergen og Farsund.

3. to-utvalgs paret t-test

• Hvis gruppene kommer fra en enkelt populasjon (f.eks. måling før og etter en eksperimentell behandling). Denne tester er ganske lik en utvalgs testen.

• Nullhypotesen (H0) er at forskjellen mellom disse gruppemiddelverdiene er null. Nullhypotese H0 : µetter - µfør = 0

• Den alternative hypotesen (Ha) er at forskjellen er forskjellig fra null. Alternativ hypotese HA : µetter - µfør ≠ 0

Testen Vi har nullhypotesen som sier at det er ingen forskjeller, H0

Figuren viser utsnitt av en tabell for t verdier. Disse finnes både i papir og digitalt format, og brukes fortsatt på enkelte læresteder, selv om de nok er på vei ut. Antall frihetsgrader er antall observasjoner minus antall datasett. Signifikansnivået som oftest brukes er 0,05 (man kan med 95% sikkerhet si at......)