Forskjell mellom versjoner av «Statistikkutkast»
| Linje 63: | Linje 63: | ||
==Case Blomsterpinner== | ==Case Blomsterpinner== | ||
| − | En blomsterpinne er en tynn pinne som man stikker ned i blomsterpotten for å støtte planten under vekst. Vi driver en bedrift og vi lager | + | En blomsterpinne er en tynn pinne som man stikker ned i blomsterpotten for å støtte planten under vekst. Vi driver en bedrift og vi lager 20 blomsterpinner om dagen. Maskinene er stilt inn sånn at pinnene skal bli 50 cm lange, men utstyret er gammelt så vi ser jo at det ikke er alle pinner som er like lange. Hvor lange er de egentlig? Og hvor mye varierer de i lengde? |
| − | Vi lager oss en populasjon i Excel. Da har vi styring på både forventningsverdi og standardavvik. Vi simulerer 10 564 pinner, setter forventningsverdien til 50 og standardavviket til | + | Vi lager oss en populasjon i Excel. Da har vi styring på både forventningsverdi og standardavvik. Vi simulerer 10 564 pinner, setter forventningsverdien til 50 og standardavviket til 3: |
[[File: 06042023-01.png]] | [[File: 06042023-01.png]] | ||
Revisjonen fra 6. apr. 2022 kl. 16:31
Utvalg
Dersom man produserer 1000 enheter av noe per dag og ønsker å sjekke kvaliteten kan det være for tidkrevende å sjekke alle 1000. Vi han ta et tilfeldig utvalg, en stikkprøve, og ved å få informasjon om utvalget kan vi forhåpentligvis si litt om hele produksjonen. Når man analyser tallmaterialet kan man selvsagt gjøre det for hånd, men det er tidkrevende og digitale hjelpemidler er gode på dette. Fordelen med å bruke regneark eller programmering er at du trolig vil treffe disse igjen etter vgs. Du kan også bruke Geogebra, men det er ikke sikkert du støter på dette programmet etter vgs.
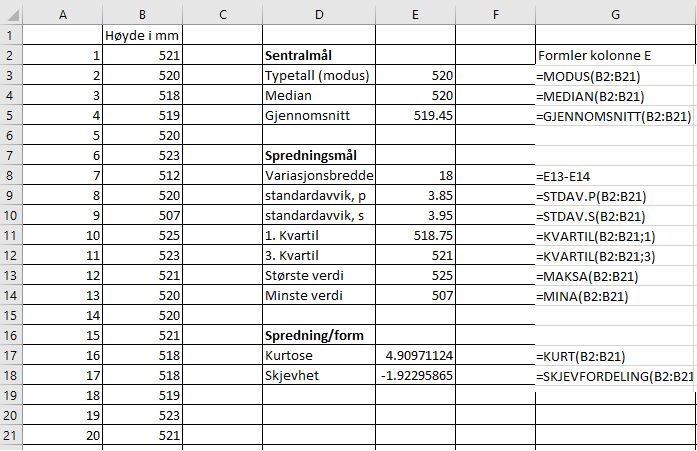
Nedenfor viser regnearket 20 tilfeldige verdier fra en produksjon på 1000. Vi ønsker å bruke de 20 enhetene til å si noe om hele dagsproduksjonen på 1000. 1000 er da populasjonen og 20 er utvalget ("sampel" på engelsk)
Her har vi tatt et utvalg på 20 fra en produksjonsserie på 1000. Vi har målt høyden på det enkelte produkt.
Begreper i statistikk
Populasjon - det totale antall individer eller objekter et sted eller over en tidsperiode. Eks: Alle harene i Nordmarka. Alle eplene produsert i Hardanger i 2023.
utvalg En del (liten) av populasjonen-
Målet er å kunne si noe fornuftig / få kunnskap om populasjoner (store mengder) på grunnlag av små mengder - utvalg.
forventningsrettet estimator
Kurtose. Normalfordelingen har kurtose 3. Høyere tall indikerer større forekomst av ekstreme verdier og motsatt.
Skjevhet. Dersom skjevheten er null er fordelingen symmetrisk
[ https://matematikk.net/side/Spredningsm%C3%A5l | Spredningsmål ]
Normalfordeling
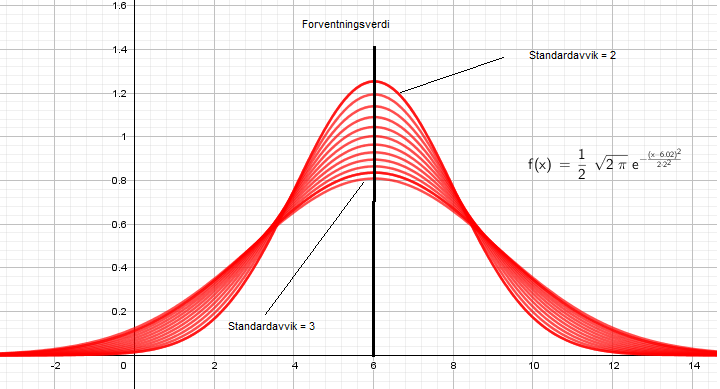
Funksjonen har en klokkeformet graf:
$f(x)= \frac{1}{\sigma \sqrt{2 \pi}} e^{- \frac{(x-\mu)^2}{2 \sigma^2}}$
der $\mu$ er forventningsverdien og $\sigma$ er standardavviket.
Figuren illustrere hvordan standardavviket påvirker klokkeformen. Grafene har standardavvik fra 3 til 2. Desto mindre standardavviket blir, desto raskere nærmer grafen seg x aksen, på begge sider av forventningsverdien.
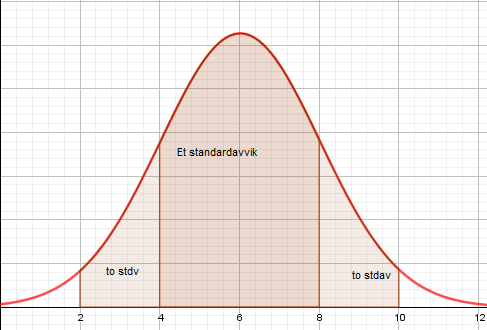
Figuren viser en normalfordeling med forventning 6 og standardavvik 2. Arealet under grafen fra x= 4 til x = 8 tilsvarer
Standardnormalfordelingen
En stokastisk variabel X med forventning $\mu =10 $ og standardavvik $\sigma = 3$ kan standardiseres ved variabelen Z.
$Z = \frac{X - \mu}{\sigma}$
Z er normalfordelt med forventning = og standardavvik 1. Z er standardnormalfordelt.
Konfidensintervall
Et intervall der vi tror en ukjent parameter ligger, kalles et konfidensintervall. Et konfidensintervall har et konfidensnivå som sier noe om hvor sannsynlig det er å finne den ukjente parameteren i intervallet. Det er vanlig å bruke et konfidensnivå på 95%, altså er det da 95% sannsynlig at parameteren man jakter på ligger i intervallet. Det er 5% sannsynlig at den ikke gjør det.
Case Blomsterpinner
En blomsterpinne er en tynn pinne som man stikker ned i blomsterpotten for å støtte planten under vekst. Vi driver en bedrift og vi lager 20 blomsterpinner om dagen. Maskinene er stilt inn sånn at pinnene skal bli 50 cm lange, men utstyret er gammelt så vi ser jo at det ikke er alle pinner som er like lange. Hvor lange er de egentlig? Og hvor mye varierer de i lengde?
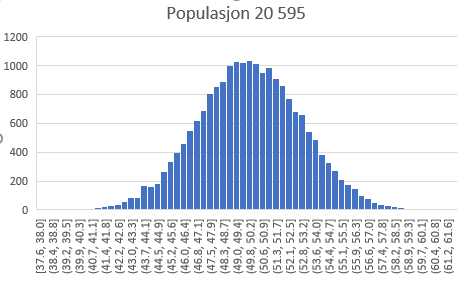
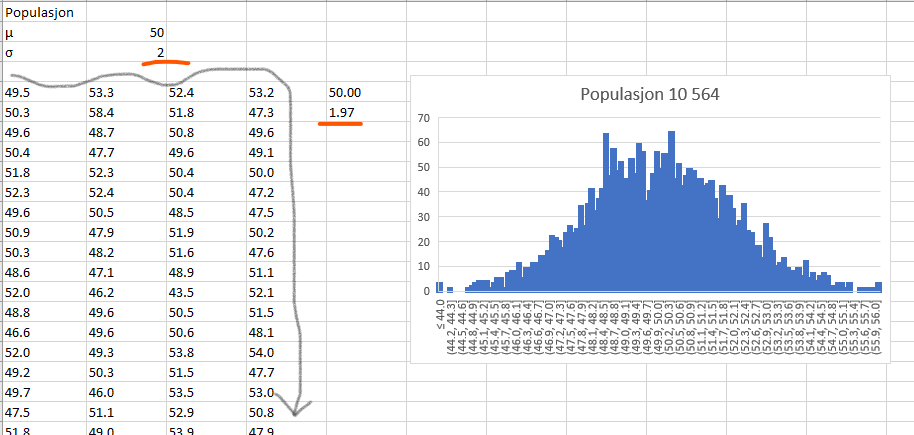
Vi lager oss en populasjon i Excel. Da har vi styring på både forventningsverdi og standardavvik. Vi simulerer 10 564 pinner, setter forventningsverdien til 50 og standardavviket til 3:
Vi ser fra figuren at søylene som angir sannsynlighetstettheten av antallet simuleringer danner en klokkeform som kan minne om en kurve lik dem over. Populasjonen har en forventning $\mu = 50$ og et standardavvik $\sigma = 1,97$.
I virkeligheten vet ikke vi noe om dette. Vi håper og tror at pinnene er 50 cm lange fordi maskinene er innstilt slik. Det tar for lang tid å måle hver enkelt pinne i hele produksjonen. Vi bestemmer oss for å måle 10 pinner en dag, 100 pinner neste dag, og 1000 pinner tredje dag, for om mulig å kunne si noe om hele populasjonen. Vi forutsetter at parameterne er like hver dag.