Forskjell mellom versjoner av «R2 2013 vår LØSNING»
| Linje 148: | Linje 148: | ||
a) Forandringen av medisinmengen vil være gitt som den totale mengden, minus hvor mye som går ut av kroppen etter hver time. | a) Forandringen av medisinmengen vil være gitt som den totale mengden, minus hvor mye som går ut av kroppen etter hver time. | ||
| − | Altså $y' = y(0) + \Delta y$, her er $y(0) = 8$, og $\Delta y = 0.05 y$. | + | Altså $y' = y(0) + \Delta y$, her er $y(0) = 8$, og $\Delta y = - 0.05 y$. |
b) | b) | ||
| Linje 172: | Linje 172: | ||
Den praktiske betydningen av dette er at mengden medisin i kroppen stabiliserer seg på $160$ gram. (Da er $y'=0$). | Den praktiske betydningen av dette er at mengden medisin i kroppen stabiliserer seg på $160$ gram. (Da er $y'=0$). | ||
Slik at det går like mye medisin inn i kroppen som ut. | Slik at det går like mye medisin inn i kroppen som ut. | ||
| − | |||
===Oppgave 2=== | ===Oppgave 2=== | ||
Revisjonen fra 3. jun. 2013 kl. 14:07
Løsning som ble utdelt til deltakerne på eksamensfest på Oslo Handelsgym 2013-05-29
Diskusjon omkring denne oppgaven
DEL EN
Oppgave 1
a) $ \displaystyle f'(x) = - 3 \sin x$
b) $ \displaystyle g'(x) = 6\pi \cos(\pi x)$
c) $ \displaystyle h'(x) = 3 \left[ 2 \sin(3x) + 3 \cos(3x) \right] e^{2x}$
Oppgave 2
a) La $u = x^2 - 4$ da er $\mathrm{d}u = 2x \, \mathrm{d}x$ slik at
$ \displaystyle \int \frac{2x}{x^2-4}\,\mathrm{d}x = \int \frac{\mathrm{d}u}{u} = \ln|u| +\mathcal{C} = \ln \left| x^2 - 4 \right| +\mathcal{C} $
b) Legg merke til at
$\displaystyle \frac{2x}{x^2-4} = \frac{x + x}{(x-2)(x+2)} = \frac{(x-2) + (x+2)}{(x-2)(x+2)} = \frac{(x-2)}{(x-2)(x+2)} + \frac{(x+2)}{(x-2)(x+2)} = \frac{1}{x+2} + \frac{1}{x-2} $
slik at vi kan skrive integralet som
$ \displaystyle \int \frac{2x}{x^2-4}\,\mathrm{d}x = \int \frac{1}{x+2} + \frac{1}{x-2} \, \mathrm{d}x = \ln \left| x + 2 \right| + \ln\left| x - 2\right| + \mathcal{C} = \ln \left| x^2 - 4 \right| +\mathcal{C} $
som ønsket.
Oppgave 3
a)
$\vec{AB} = (2,2,0)$ og $\vec{AC} = (-1,1,0)$ slik at $\vec{AB} \times \vec{AC} = (-1,-1,4)$.
Arealet blir da følgelig
$ \displaystyle A = \frac{1}{2} \left| \vec{AB} \times \vec{AC} \right| = \frac{1}{2} \sqrt{ (-1)^2 + (-1)^2 + 4^2 } = \frac{3}{2} \sqrt{2} $
a)
$ \vec{AB} \cdot \vec{AC} = 2 \cdot (-1) + 2 \cdot 1 + 0 = 0 $
Arealet blir da følgelig
$\displaystyle A = \frac{1}{2} \left| \vec{AB} \right| \cdot \left| \vec{AC} \right| = \frac{1}{2} \cdot 3 \cdot \sqrt{2} = \frac{3}{2} \sqrt{2} $
som før.
Oppgave 4
$ \displaystyle \begin{align*} y' & = 6x y \\ \frac{1}{y} \frac{\mathrm{d}y}{\mathrm{d}x} & = 6 x \\ \int \frac{\mathrm{d}y}{y} & = \int 6x \mathrm{d}x \\ \ln |y| & = 3 x^2 + \mathcal{C}_1 \\ y & = \pm \mathcal{C}e^{3x^2} \end{align*} $
Grensebetingelense gir at $y(0) = C$ og $y(0) = 2$ så $C$ = 2. Her må $C$ være positiv, siden ellers løser den ikke den opprinnelige differensiallikningen ($y' = 6x \cdot y$)..
Oppgave 5
a)
Bare å telle videre $a_{16} = 31$. Bare å summere alle leddene $S_{16} = 16^2 = 256$.
b)
Følgen har en fast differanse, og er dermed aritmetisk.
$a_n = 2n - 1$ og $S_n = n^2$.
c)
$S_n > 400 $ som er det samme som $n^2 > 400$ slik at $n>20$.
Oppgave 6
Oppgave 7
La $V(n) = a + ak+ \ldots + a k^{n-1}$ og $\displaystyle H(n) = a \cdot \frac{k^n-1}{k-1}$.
$V(1) = a \cdot k^{1-1} = a$ og $\displaystyle H(1) = a \cdot \frac{k^1-1}{k-1} = a$.
Formelen stemmer altså for $n=1$. Anta at formelen holder for $n = m$. Altså at $V(m) = H(m)$ stemmer, for en eller annen $m$. Ønsker da å vise at dette medfører at $V(m+1) = H(m + 1)$. Utregning av $V(m + 1)$ gir
$ \displaystyle \begin{align*} V(m+1) & = V(m) + a k^{m} \\ & = \left( a + ak + ak^2 + \ldots + a k^{m-1} \right) + a k^{m} \\ & = H(m) + a k^{m} \\ & = a \cdot \frac{k^{m} - 1}{k - 1} + a k^{m} \\ & = a \cdot \frac{k^{m} - 1 + (k - 1) \cdot k^{m} }{k - 1} \\ & = a \cdot \frac{k \cdot k^{m} - 1 }{k - 1} \\ & = a \cdot \frac{k^{m + 1} - 1}{k - 1} \end{align*} $ Regner vi ut $H(m+1)$ ser vi raskt at $ \displaystyle H(m + 1) = a \cdot \frac{k^{m + 1} - 1}{k - 1} $. og resten følger ved induksjon.
DEL TO
Oppgave 1
a) Forandringen av medisinmengen vil være gitt som den totale mengden, minus hvor mye som går ut av kroppen etter hver time. Altså $y' = y(0) + \Delta y$, her er $y(0) = 8$, og $\Delta y = - 0.05 y$.
b)
$ \displaystyle \begin{align*} y' & = 8 - \frac{1}{20} y \\ 20 y' & = - (y - 160) \\ \int \frac{\mathrm{d}y}{y - 160} & = - \frac{1}{20} \mathrm{d}t \\ \ln \left| y - 160 \right| & = - \frac{t}{20} + \mathcal{C}_1 \\ y & = \mathcal{C} e^{-\frac{t}{20}} + 160 \end{align*} $
Eventuelt funker det å bruke integrerende faktor. Ser at $y(0) = C$, slik at $C=160$.
[size=100] c)
Legg merke til at $e^{-a} = 1/e^a$, slik at når $a$ vokser går $e^{-a}$ mot null for alle positive a. Slik at
$\lim_{t \to \infty} y = 160$
Den praktiske betydningen av dette er at mengden medisin i kroppen stabiliserer seg på $160$ gram. (Da er $y'=0$). Slik at det går like mye medisin inn i kroppen som ut.
Oppgave 2
a)
b)
$ f(x) =12 e^{-x/2} \cdot \sin(x/2) $. Derivasjon gir oss
$ f'(x) = -6\frac{1}{2} e^{-x/2}\cdot \big( \sin(x/2) - \cos(x/2) \big) $
Løser vi denne likningen fås
$\tan(x/2) = 1$, som har løsninger $x/2 = \pi n + \pi /4$
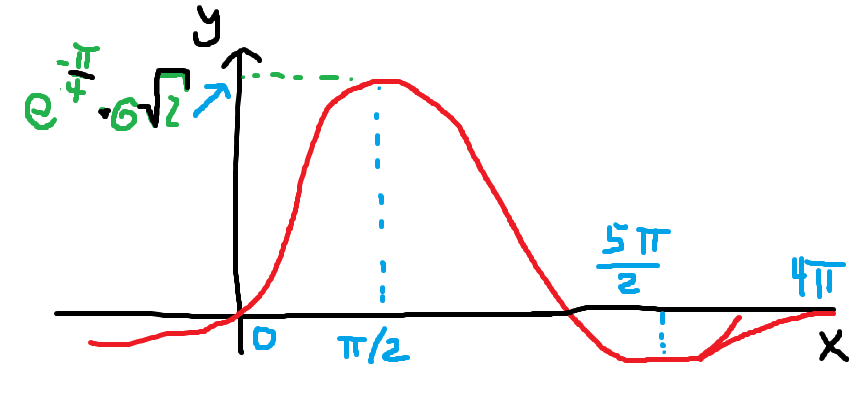
Slik at løsningene blir $x = 0$, $x= \pi/2$ og $x = 5\pi/2$ og $\pi/4$.
Hvor $x=0$ og $x=4\pi$ er lokale bunnpunkt, mens $x=\pi/2$ er toppunkt og $x=5\pi/2$ er bunnpunkt.
$(0,0)$ , $(\pi/2,3.8687)$, $(5\pi/2,-0.16718)$ og $(4\pi,0)$.
Tegning av fortegnskjema + figur viser dette greit..
c)
Funksjonen er positiv frem til $x=2\pi$, siden $\sin(\pi)=0$ og $\sin(0)=0$. Videre så er funksjonen negativ fra $x=2\pi$ til $x=4\pi$ Så det toalet arealet avgrenset av $x$-aksen og funksjonen er
$ \displaystyle \begin{align*} I & = \int_0^{4\pi} \big| f(x) \big| \, \mathrm{d}x \\ & = \int_0^{2\pi} f(x) \, \mathrm{d}x - \int_{2\pi}^{4\pi} f(x) \, \mathrm{d}x \\ & = \int_0^{2\pi} f(x) \, \mathrm{d}x + \int_{0}^{2\pi} e^{-\pi} f(x) \, \mathrm{d}x \\ & = 12 \left( 1+e^{-\pi} \right) \int_0^{2\pi} e^{-x/2} \sin(x/2) \, \mathrm{d}x \\ & = 24 \left( 1+e^{-\pi} \right) \int_0^{\pi} e^{-u} \sin u \, \mathrm{d}u \\ & = 24 \left( 1+e^{-\pi} \right) \left[ \frac{1}{2}e^{-u} \left( \cos u + \sin u\right) \right]_{\pi}^0 \\ & = 12 \left( 1+e^{-\pi} \right) \left[ e^{0}( 1 + 0) - e^{-\pi}(-1+ 0) \right] \\ & = 12 \left( 1+e^{-\pi} \right) \left( 1 + e^{-\pi} \right) \\ & = 12 \left( 1 + e^{-\pi/2} \right)^2 \approx 13.05954335 \end{align*} $
Brukte så substitusjonen $u = x/2$, også formel. For å se den andre overgangen brukes det at $\sin x$ er periodisk, med substitusjonen $u = x - 2\pi$ hvor $\mathrm{d}x = \mathrm{d}u$
$ \displaystyle I \int_{2\pi}^{4\pi} e^{-x/2} \sin(x/2) \, \mathrm{d}x = \int_{2\pi-2\pi}^{4\pi-2\pi} e^{-\pi-u/2} \sin\left( \frac{u}{2} + \pi\right) \, \mathrm{d}u = - e^{-\pi} \int_0^{2\pi} e^{-u/2} \sin(u/2) \, \mathrm{d}u = - e^{-\pi} \int_0^{2\pi} f(x) \, \mathrm{d}x $
Hvorfor $ \displaystyle \sin\left( \frac{u}{2} + \pi\right) = - \sin\left( \frac{u}{2} \right) $, kan du selv få finne ut av ved å bruke addisjonsformelen for sinus =)
Oppgave 3
a)
$AD = (-3,0,4)$ og $AB = (0,3,0)$, ser at $AD \cdot AB = 0$ slik at arealet av sideflaten blir
$\triangle ABD = \frac{1}{2}|AD||AB| = \frac{1}{2} \cdot 3 \cdot 5 = 7 + \frac{1}{2}$.
b)
Normalvektoren til planet er blir $AB \times AC = [12,0,9] = [4,0,3]$, slik at likningen for planet blir
$ 4(x-3) + 0(y-0) + 3(z-0) = 4x + 3z - 12 $
som ønsket.
c)
Korteste avstand fra origo til et plan, vil være ei linje som er paralell med normalvektoren. Altså linja
$ l(t) = (0,0,0) + (4,0,3)t $
Setter vi denne likningen inn i planlikningen og løser fås
$ 4(4t) + 3(3t) - 12 = 0 \rightarrow t = 12/25 $.
Insatt fås altså at korteste avstand blir
$ \displaystyle d = \sqrt{ \left( 4 \cdot \frac{12}{25} \right)^2 + 0^2 +\left( 3 \cdot \frac{12}{25} \right)^2 } = 12/5 $
Eventuelt bruk punkt plan formelen.
$ \displaystyle \begin{align*} d & = \frac{ a \cdot x_0 + b \cdot y_0 + c \cdot z + d }{ \sqrt{ a^2 + b^2 + c^2 } } \\ & = \frac{ \left| 3 \cdot 0 + 0 + 4 \cdot 4 - 12 \right| }{ \sqrt{ 3^2 + 0^2 + 4^2 } } \\ & = \frac{12}{5} \end{align*} $
samme som før.
d)
Normalvektorene kan skrives som $n_1 = (4,0,3)$ og $n_2=(4,3,0)$ slik at
$ \displaystyle \cos \theta = \frac{n_1 \cdot n_2}{ \left| n_1 \right| \cdot \left| n_2 \right| } = \frac{9}{25} $
Slik at
$ \displaystyle \theta = \arccos \left( \frac{9}{25} \right) \approx 68.89980395 $
Stemmer ikke med tegningen min hvor jeg får $55.55$.. Men er sikkert noen som klarer og oppdage feilen min.
Oppgave 4
a)
$y$ koordinaten til $C$ vil være den samme som til $A$, slik at $2^2 + y^2 = 3^2 \Rightarrow y = \sqrt{5}$, da avstanden må være positiv.
$y(x) = \frac{\sqrt{5}}{2}x + b$, siden funksjonen går igjennom origo er $b=0$. Og stigningstallet var $a = (y_1-y_0)/(x_1-x_0) = y_1/x_1$.
b)
$ \displaystyle \begin{align*} F_1 = \pi \int_0^2 \left( \frac{ \sqrt{5}}{2} x \right)^2 \mathrm{d}x = \pi \left[ \frac{25}{12} x^3 \right]_0^2 = \frac{ 10 \pi }{ 3 } \end{align*} $
c)
Tilsvarende som i b) fås
$ \displaystyle \begin{align*} F_1 & = \pi \int_2^3 \left( \sqrt{ 9 - x^2 } \right)^2 \mathrm{d}x \\ & = \pi \left[ \frac{x}{3} \left( 27 - x^2 \right) x^3 \right]_2^3 \\ & = \frac{3}{3} \left( 18 \right) - \frac{2}{3} \left( 23 \right) \\ & = \frac{54 - 46}{3} \pi = \frac{ 8 \pi }{ 3 } \end{align*} $
Oppgave 5
a)
Omkretsen er alle sidene lagt sammen, og siden vi har et rektangl er omkretsen gitt som
$ O = 2x + 2y = 2 D \cos v + 2 D \sin v $.
Hvor en benyttet seg av definisjonen av cosinus og sinus. $\cos v = x/D$ og $\sin v = y/D$
Tilsvarende så er
$ A(v) = \cdot x \cdot y = D^2 \cos v \cdot \sin v = \frac{1}{2} D^2 \sin (2v) $
b)
Derivasjon gir enkelt og greit at
$ \displaystyle O(x) = 2D \cdot \cos v - 2D \cdot \sin v = 2x - 2y $
Herfra ser vi at $O'(x)$ er null når $x=y$, altså når rektangelet er et kvadrat. Dette kan ikke være et bunnpunkt som en kan se fra en fin fortegnslinje.
Maks areal blir dermed
$ O(x) = 2 D \cos 45 + 2 D \sin 45 = 2 \sqrt{2} D $.
Hvor en brukte at de indre vinklene i et kvadrat er $90$ grader slik at diagonalene kutter disse i to og følgelig er $v = 45$ grader. Dette kan og vises ved å løse $O'(x) =0$.
c)
Ser at
$A'(x) = - D^2 \cos 2v$, som er null når $v=\pi/4 = 45^\circ$, altså når vi har et kvadrat. En kan da og sette inn og se at $x = y$.
$ A(x) = \frac{1}{2} D^2 \sin (2v) $ Denne er maksimal når $\sin(2v)$ er maksimal som er $1$. Da er $A(x) = \frac{1}{2} D^2 $, eventuelt bruker en at $\sin(2 \cdot \pi/4) = 1$.
Oppgave 6
a)
Legg merke til at rekken er geometrisk og at
$\displaystyle d = \frac{3}{4}$
(Husk at du må sjekke alle leddene her)
Siden rekken er geometrisk og $d = 3/4 < 1$ så konvergerer rekken. Slik at summen av rekken blir dermed
$ \displaystyle S = A \cdot \frac{1}{1 - \frac{3}{4}} = 4 A $.
a)
Ved å øke antall trekanter (gå til neste figur), halveres sidelengden i trekanten hver gang. Slik at
$ O_2 = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{3}{2} a $ Siden det er tre av disse trekantene må vi gange med $3$ og får da $9a/2$.
For hver gang halverer vi sidekantene og ganger antall trekanter med $3$, slik at i trekant $n$ har vi
$ \displaystyle \begin{align*} O_n & = 3^n \left( \frac{a}{2^n} + \frac{a}{2^n} + \frac{a}{2^n} \right) \\ & = 3 \cdot \left( \frac{3}{2} \right)^n \cdot a \end{align*} $
Merk at siden $3>2$ så vil $3^n$ øke raskeren enn $2^n$ slik at når $n$ øker vil $(3/2)^n$ gå mot uendelig. Konklusjonen blir dermed at $O_n \to \infty$ når $n\to \infty$.
Dette forteller at selv om arealet av Sierpiński-trekanten er endelig, er ikke omkretsen av den endelig!
Dette er en oppgave i samme gate som http://en.wikipedia.org/wiki/Gabriel%27s_Horn =)