R2 2010 vår LØSNING
Oppgave 2
a)
<tex> \vec{AB} = [-3, 2, 2] </tex> og <tex> \vec{AC} = [-2, -1, 6] </tex>
<tex> \vec{AB} \times \vec{AC} = [12+2,-(-18+4), 3+4]= [14, 14, 7] </tex>
b)
Normalvektoren til planet som går gjennom punktene A, B og C er <tex> \frac17[14, 14, 7] = [2, 2, 1]</tex>
Ett vilkårlig punkt i planet er P= (x,y,z).
<tex> \vec{AP} \cdot \vec{n} = 0 , [x-3 , y-0, z+2] \cdot [2, 2, 1] = 0 </tex>
<tex> \alpha: 2x + 2y + z - 4 = 0 </tex>
c)
Siden linjen står vinkelrett på alfa planet kan vi bruke [2, 2, 1] som rettningsvektor for linjen l. Linjen går gjennom P = (5, 4, 4). Man får da:
[x,y,z] = [5, 4, 4] + t [2, 2, 1] som er ekvivalent med <tex> n: \left [ x = 5+ 2t\\ y = 4 + 2t \\
z = 4 + t \right]</tex>
I xz-planet er y = 0. Parameterfremmstillingen for linjen gir da t=-2. Innsatt for x og z gir det koordinatene (1, 0 2)
d)
Et vilkårlig punkt Q på linjen l er gitt ved parameterfremstillingen for l. Man får:
<tex> V_{ABCQ} = \frac16|(\vec{AB} \times \vec {AC}) \cdot \vec{AQ}|</tex>
<tex> \vec{AQ}= [5+2t-3, 4+2t-0, 4+t+2] = [2t+2, 2t+4, t+6] </tex>
innsatt i likningen over gir det:
<tex> V_{ABCQ} = \frac16|[14, 14, 7] \cdot [2t+2, 2t+4, t+6] | = \frac73|5t+12|</tex>
e)
Volumet i pyramiden skal være 42. Innsatt svaret i d gir det |5t+12|= 18 som gir
5t + 12 = 18 eller 5t + 12 = -18
<tex>t = \frac{6}{5}</tex> eller <tex>t = 6</tex>
Man får to løsninger, en "over", og en "under" alfa- planet. Man setter inn i parameterframstillingen for l og får:
<tex> Q= ( \frac{37}{5}, \frac{32}{5}, \frac{26}{5})</tex> eller Q = (-7, -8, - 2).
Del 2
oppgave 3
oppgave 4
<tex> f(x)=5e^{-0,2x} \cdot (sinx + cosx) </tex> der <tex> x \in <0,15> </tex>
a)
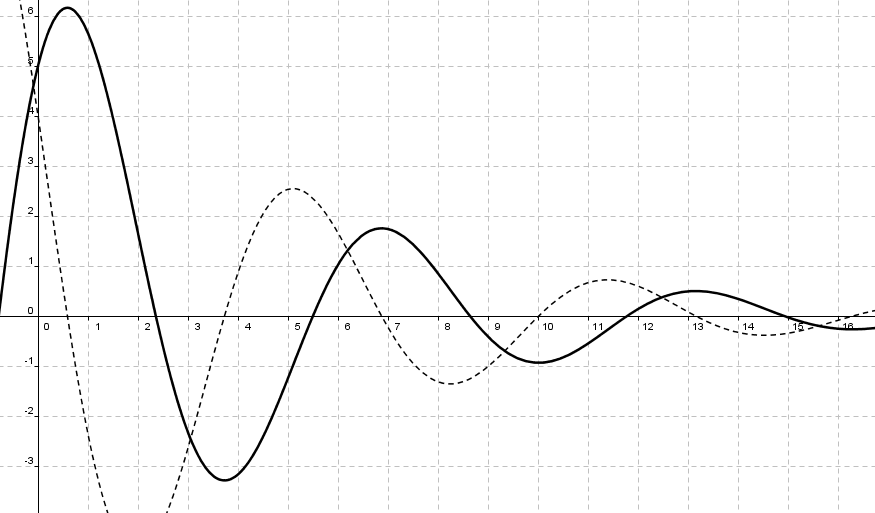
Grafen ser slik ut:
Den deriverte er også med (stiplet) fordi den skal finnes i c.
b)
Nullpunkter
f(x)=0
<tex> 5e^{-0,2x}</tex> kan aldri bli null. Man får
<tex>sinx +cosx =0 \\ tanx = -1\\ x= \frac{3\pi}{4} + n \cdot \pi\\ x \in (( \frac{3\pi}{4},0), (\frac{7\pi}{4},0),(\frac{11\pi}{4},0),(\frac{15\pi}{4},0),(\frac{19\pi}{4},0))</tex>
Regner man om fra eksakte verdier, til desimaltall, ser man at det stemmer med grafen i a.
c)
<tex> f'(x)=5(-0,2)e^{-0,2x} \cdot (sinx + cosx)+5e^{-0,2x} \cdot (cosx -sinx)\\ = -e^{-0,2x} \cdot sinx -e^{-0,2x} \cdot cosx +5e^{-0,2x} \cdot cosx - 5e^{-0,2x} \cdot sinx \\ 4e^{-0,2x} \cdot cosx - 6e^{-0,2x} \cdot sinx =2e^{-0,2x} \cdot (2cosx-3sinx) </tex>
d)
Man har et toppunkt hver gang den deriverte skifter fortegn fra positiv til negativ. Ved å løse 2cosx - 3sinx = 0 og å tegne fortegnslinje, finner man at det er tilfelle for x=0,59 , x=6,87 og for x= 13,15. Sett disse x verdiene inn i funksjonsuttrykket og man får funksjonsverdien til toppunktene.
e)
<tex> A= \sqrt{a^2 + b^2} = \sqrt2</tex> Punktet (1,1) ligger i første kvadrant.<tex>tan \phi = 1</tex> Man får da:
<tex> f(x)=5e^{-0,2x} \cdot \sqrt2\cdot sin(x + \frac{\pi}{4}) = 5\sqrt2e^{-0,2x} \cdot sin(x + \frac{\pi}{4}) </tex>
f)
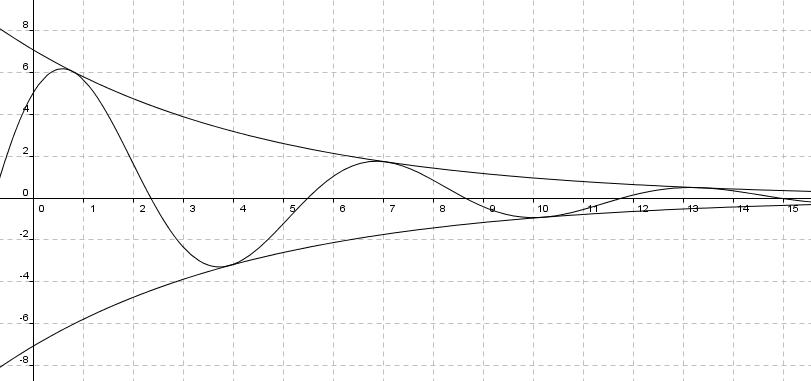
<tex>sin(x + \frac{\pi}{4}) </tex> varier i verdi mellom -1 og 1, avhengig av x. Derfor ligger f mellom q og p, altså i området <tex> \pm5\sqrt2e^{-0,2x}</tex>