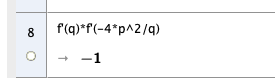Forskjell mellom versjoner av «R1 -H19-opg4»
Fra Matematikk.net
(→b)) |
|||
| (5 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 4: | Linje 4: | ||
===LØSNING=== | ===LØSNING=== | ||
| + | ===a)=== | ||
[[File:r1-h19-s1.png ]] | [[File:r1-h19-s1.png ]] | ||
Her er det brukt flere linjer enn strengt tatt nødvendig, men jeg tenker det gir oversikt. | Her er det brukt flere linjer enn strengt tatt nødvendig, men jeg tenker det gir oversikt. | ||
| − | Definerer først funksjonen f. Definere så punktene P og Q. Lager så linjen gjennom P og Q. Setter linjen lik f for å finne felles punkter. | + | Definerer først funksjonen f. Definere så punktene P og Q. Lager så linjen gjennom P og Q. Setter linjen lik f for å finne felles punkter. x = q var jo utgangspunktet. Det andre punktet er $x = - \frac{4p^2}{q}$, som er x koordinaten til punktet R. |
| + | |||
| + | |||
| + | |||
| + | ===b)=== | ||
| + | |||
| + | Dersom to linjer i et koordinatsystem står normalt på hverandre er produktet av stigningstallene -1. Den deriverte gir oss stigningstallet: | ||
| + | |||
| + | [[File:r1-h19-s2.png ]] | ||
| + | |||
| + | Altså står linjene normalt på hverandre. | ||
| + | |||
| + | [[CAS |tilbake ]] | ||
Nåværende revisjon fra 17. mar. 2020 kl. 07:27
LØSNING
a)
Her er det brukt flere linjer enn strengt tatt nødvendig, men jeg tenker det gir oversikt.
Definerer først funksjonen f. Definere så punktene P og Q. Lager så linjen gjennom P og Q. Setter linjen lik f for å finne felles punkter. x = q var jo utgangspunktet. Det andre punktet er $x = - \frac{4p^2}{q}$, som er x koordinaten til punktet R.
b)
Dersom to linjer i et koordinatsystem står normalt på hverandre er produktet av stigningstallene -1. Den deriverte gir oss stigningstallet:
Altså står linjene normalt på hverandre.