Praktisk romgeometri

Nedenfor finner man en oversikt over de vanligste spørsmål som dukker opp i forbindelse med punkter, linjer og plan.

Punkt

Avstand mellom to punkter

Avstanden d mellom punktene A og B er gitt ved <tex>d=|\vec{AB}|= \sqrt{(x_B - x_A)^2 + (y_B -y_A)^2 + (z_B - z_A)^2} </tex>

Altså lik lengden av AB vektor.

Eks:

Gitt er punktene P = (1,2,3) og Q = (4,4,2). Hva er avstanden mellom P og Q?

<tex>d = \sqrt{(4 - 1)^2 + (4 -2)^2 + (2 - 3)^2} = \sqrt{9+4+1} = \sqrt{14}</tex>

Linje

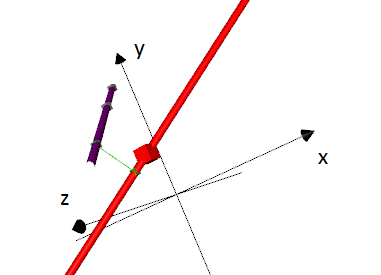
En rett linje m som går gjennom punktet <tex>p = (x_0 , y_0 , z_0) </tex> og har rettningsvektor <tex> \vec{n} = (a, b, c) </tex> har parameterfremstillingen: <tex> m: \left [ x = x_0 + at\\ y = y_0 + bt \\ z = z_0 + ct \right]</tex>

I plantet er det slik at to linjer som ikke er parallelle vil skjære hverandre. I rommet er det nødvendigvis ikke tilfelle. To linjer som ikke er parallelle og som ikke skjærer hverandre sies å være vindskeive.

---

Skjæring mellom linjer

Dersom to linjer i rommet skjærer hverandre må det være en parameterverdi for hver av linjene som gir et felles punkt, dvs. samme x-, y-, og z koordinat for begge linjene.

Eks:

Vi har gitt linjene:

<tex> m: \left [ x = -1-s\\ y = 3+s \\ z = -s \right]</tex> og <tex> n: \left [ x = 3-2t\\ y = t \\

z = 1+t \right]</tex>

Skjærer linjene hverandre?

<tex>-1-s = 3-2t \quad \wedge \quad 3+s = t \\ s = -2 \quad \wedge \quad t =1 </tex>

Innsatt s = - 2 i linje m gir det punktet (1, 1, 2), og innsatt t = 1 i linje n gir (1, 1, 2). Konklusjonen er at m og n skjærer hverandre i punktet (1, 1, 2).

---

Avstand mellom punkt og linje

A er et vilkårlig punkt på linjen l. P er et punkt som ikke ligger på linjen. Arealformelen med vektorproduktet gir:

<tex> T = \frac12 \cdot | \vec{AP} \times \vec{v}| </tex>

Der <tex>\vec{v}</tex> er rettningsvektoren til l.

Fra ingdomsskolen har man at arealet av en trekant er: <tex>T = \frac12 \cdot g \cdot h = \frac12 \cdot |\vec{v}| \cdot h </tex>

h er høyden i trekanten, altså den rette linjen fra punktet P som står normalt på linjen l, altså den avstanden man ønsker å finne. Kombinert gir dette:

<tex> \frac12 \cdot |\vec{v}| \cdot h = \frac12 \cdot | \vec{AP} \times \vec{v}|</tex>

<tex> |\vec{v}| \cdot h = | \vec{AP} \times \vec{v}|</tex>

<tex> h = \frac{ | \vec{AP} \times \vec{v}|}{|\vec{v}|}</tex>

Eks:

Finn avstanden mellom linjen <tex> m: \left [ x = -1-s\\ y = 3+s \\

z = -2s \right]</tex> og punktet P =(1, 1, 2)

Punktet A =(-1, 3, 0) ligger på linjen m. Da er

<tex>\vec{AP}=[2, -2, 2] \quad og \quad \vec{v} = [-1, 1, -2]</tex>

<tex> h = \frac{ | \vec{AP} \times \vec{v}|}{|\vec{v}|} = \frac{ | [2, -2, 2] \times [-1, 1, -2]|}{|[-1, 1, -2]| } =\frac{2}{\sqrt{3}} </tex>

---

Ligger punktet på linja?

Man finner først den parameterverdien som gir planets x verdi lik punktets x verdi. Dersom denne parameterverdien gir tilsvarende verdier for plantes y og z koordinat ligger punktet i planet.

En linje er gitt som <tex> m: \left [ x = -1-s\\ y = 3+4s \\

z = -s \right]</tex> Ligger punktet P =(4,-17,5) på linjen?

4=-1-s gir s = -5 innsatt s=-5 for y gir y = 3 +4(-5) = -17 og z = -(-5)= 5 hvilket betyr at punktet ligger på linjen.

---

Avstand mellom to linjer

Først finner man ut om de to linjene er parallelle, eller om de er vindskeive.

Dersom de er paralelle ser man det ved at rettningsvektoren til den ene linjen er lik rettningsvektoren til den andre multiplisert med en konstant.

PARALLELLE:

Man velger et punkt på hver av linjene (A og P) og setter inn i:

<tex> h = \frac{ | \vec{AP} \times \vec{v}|}{|\vec{v}|}</tex>

Eks:

<tex> m: \left [ x = -1-s\\ y = 3+s \\ z = -2s \right]</tex> og <tex> n: \left [ x = 1+t\\ y = 1-t \\

z = 2+2t \right]</tex> er paralelle linjer.

A = (-1, 3, 0) er et punkt på m, og P = (1, 1, 2) er et punkt på n. Rettningsvektor for m er [-1, 1, -2]. Vi får da:

<tex> h = \frac{ | \vec{AP} \times \vec{v}|}{|\vec{v}|} = \frac{ | [2, -2, 2] \times [-1, 1, -2]|}{|[-1, 1, -2]| } =\frac{2}{\sqrt{3}} </tex>

VINDSKEIVE: For å finne avstanden mellom to vindskeive linjer må man finne lengden av den linje som står vinkelrett på begge de to vindskeive linjene.

Eks:

Finn avstanden mellom m og n. <tex> m: \left [ x = -1-s\\ y = 3+s \\ z = -2s \right]</tex> og <tex> n: \left [ x = 1+t\\ y = 1+t \\ z = 2-t \right]</tex>

Rettningsvektorene er <tex>\vec{v_m}= [-1,1,-2] </tex> og <tex> \vec{v_n}= [1,1,-1] </tex>

Man må så finne punktene på m og n som forbinder de to linjene med et linjestykke som står normalt på både m og n.

<tex>P_m = (-1-s, 3+s, -2s) </tex> og <tex>P_n = (1+t, 1+t, 2-t) </tex> som gir <tex>\vec{P_mP_n} = [1+t+1+s, 1+t-3-s, 2-t+2s]

= [2+t+s, -2+t-s, 2-t+2s] </tex>

Da må

<tex>\vec{v_m} \perp \vec{P_mP_n}</tex> og <tex>\vec{v_n} \perp \vec{P_mP_n}</tex>

som gir

<tex>\vec{v_m} \cdot \vec{P_mP_n} = 0</tex> og <tex>\vec{v_n} \cdot \vec{P_mP_n} = 0</tex>

<tex>[-1,1,-2] \cdot [2+t+s, -2+t-s, 2-t+2s] = 0</tex> og <tex> [1,1,-1] \cdot [2+t+s, -2+t-s, 2-t+2s] = 0</tex>

<tex>-2-t- s-2+t-s-4+2t-4s = 0</tex> og <tex>2+t-s-2+t-s-2+t-2s =0</tex>

<tex>-8+2t-6s = 0</tex> og <tex>-2 +3t -2s =0</tex>

<tex>t= 3s+4</tex> og <tex>-2+3(3s+4)-2s = 0</tex>

<tex>t= 2s+4</tex> og <tex>10+9s = 0</tex>

<tex>t= 2s+4</tex> og <tex>s= - \frac{10}{7}</tex>

<tex>t= - \frac 27</tex> og <tex>s= - \frac{10}{7}</tex>

Innsatt gir det

<tex>\vec{P_mP_n} = [\frac27 ,- \frac 67, - \frac47 ]</tex>

Avstanden mellom linjene blir da 1,07

Situasjonen ser slik ut:

Avstanden er den tynne streken mellom de to noe tykkere linjene, laget i Autograph.

---

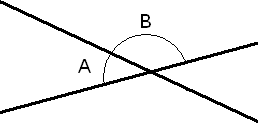
Vinkel mellom to linjer

Vinkelen man søker er A. Man finner vinkelen mellom to linjer ved å finne vinkelen mellom rettningsvektorene (skalarprodukt). Den største vinkelen mellom to linjer er 90 grader. Dersom den vinkelen man finner er større enn 90 grader (B), tar man 180 - B = A, som er den man ønsker å finne.

Eks:

Finn vinkelen mellom m og n. <tex> m: \left [ x = -1-s\\ y = 3+s \\ z = -2s \right]</tex> og <tex> n: \left [ x = 1+t\\ y = 1+t \\ z = 2-t \right]</tex>

Rettningsvektorene er <tex> \vec{v_m} = [-1,1,-2] </tex> og <tex> \vec{v_n} = [1,1,-1] </tex>

<tex>cos \alpha = \frac{ \vec{v_m} \cdot \vec{v_n}}{ |\vec{v_m}| \cdot |\vec{v_n}|} = \frac{ [-1,1,-2] \cdot [1,1,-1]}{ \sqr{6} \cdot \sqr{3}} = \frac{2}{ \sqr{18}} </tex>

<tex> \alpha = 61,9^{\circ} </tex>

---

Ligger punktet på linja?

Desom et bestemt punkt ligger på linjen betyr det at en og samme parameterverdi innsatt for x, y og z koordinatene i parameterfremstillingen for linja, gir koordinatene til punktet.

Eks:

En linje er gitt ved: <tex> l: \left [ x = 1 + 3t\\ y = 2 + 2t \\ z = 2 + t \right]</tex>

Ligger punktet P = (-2, 0, 1) på linjen l ?

Man setter inn x=-2 og får t = - 1. Innsatt t = -1 for y og z gir hennoldsvis y = 0 og z = 1, hvilket betyr at P ligger på l

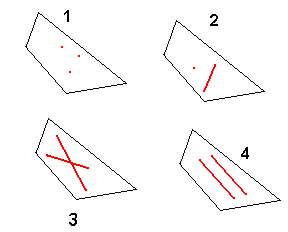
Plan

Et plan er definert ved

(1) tre punkter

(2) ett punkt og en linje

(3) to linjer som krysser hverandre

(4) to parallelle linjer

Disse tilfellene er sider av samme sak, man trenger et punkt i planet og informasjon til å finne normalvektor, kryssproduktet mellom to ikke-parallelle vektorer i planet.

Likningen for et plan er:

<tex> a(x-x_0)+b(y-y_0)+c(z-z_0)=0 \\

ax+by+cz+d=0</tex>

Der a,b og c er koordinatene til planets normalvektor, og<tex>x_0,y_0,z_0</tex> er et punkt i planet.

Parameterfremmstillingen for et plan er gitt ved

<tex> \alpha: \left [ x = x_0 + u_xs+v_xt\\ y = y_0 + u_ys+v_yt \\

z = z_0 + u_zs+v_zt \right]</tex>

Der u og v er vektorer i planet (ikke parallelle).

---

Vinkel mellom linje og plan

Vinkelen mellom en linje og en plan finner man ved å benytte skalarproduktet mellom rettningsvektoren for linja og normalvektoren for planet.

---

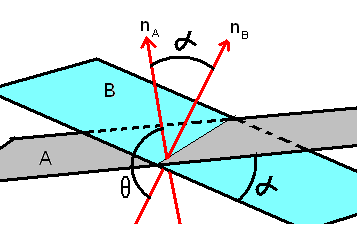
Vinkelen mellom to plan

Vinkelen mellom to plan er den samme som den minste vinkelen mellom planenes normalvektor.

---

Avstand linje og plan

Dersom en linje er paralell med planet vil den aldri skjære planet. Det kan da være av interese å finne avstanden mellom linjen og planet.

---

Avstand mellom punkt og plan

Man trenger likningen til planet og koordinatene til punktet.

Dersom planet er gitt ved <tex> ax+by+c + d = 0</tex> og punktet gitt som <tex> P = (x_p, y_p, z_p)</tex>

er avstanden s mellom punkt og plan gitt som

<tex> s = \frac{|ax_p+by_p+cz_p + d|}{\sqrt{a^2+b^2+c^2}}</tex>

Eks

Et plan har likningen <tex> 2x-y+z-3=0 </tex> og punktet P har koordinatene (2, 2, 3). Finn avstanden fra P til planet

<tex> s = \frac{|ax_p+by_p+cz_p + d|}{\sqrt{a^2+b^2+c^2} }= \frac{|2 \cdot 2 + (-1)\cdot 2 + 1 \cdot 3 - 3|}{\sqrt{2^2+(-1)^2+1^2}} = \frac{|4 -2 + 3 - 3|}{\sqrt{6}}= \frac{2}{\sqrt{6}} </tex>

---

Skjæring mellom to plan

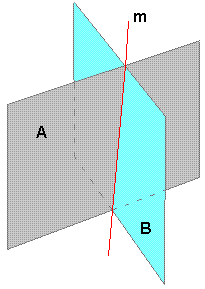Dersom to plan ikke er parallelle vil de før eller senere skjære hverandre og danne en rett linje. For å finne uttrykket for linjen gjøres følgende: Ta vektorproduktet av planenes normalvektorer, det gir linjens retningsvektor. Sett så inn en vilkårlig x verdi (samme) i begge plans ligninger. Det gir to ligninger med to ukjente. Løs for y og z og man har et punkt på linjen.

Eks:

Vi har planet A: 2x + 3y - z + 3 = 0 og plan B: 4x + 5y + z - 1 = 0

med tilhørende normalvektorer: nA = [2,3,-1] og nB = [4,5,-1]

Man finner retningsvektor til skjæringslinjen ved å ta vektorproduktet til normalvektorene:

nA x nB = [(3+5),(-4-2),(10-12)] = [8,-6,-2] = 2[4,-3,-1]

[4,-3,-1] er en retningsvektor for skjæringslinjen.

I ligningene for plan A og B setter vi x=1 og får:

2 -3y - z + 3 = 0 og 4 + 5y + z - 1 = 0

som gir y = -1 og z = 2 det gir punktet P(1,-1,2)

Skjæringslinjen er da bestemt til: [x,y,z] = [1,-1,2] +t[4,-3,-1] som er det samme som parameterframstillingen:

x = 1 + 4t

y = -1 - 3t

z = 2 - t

---

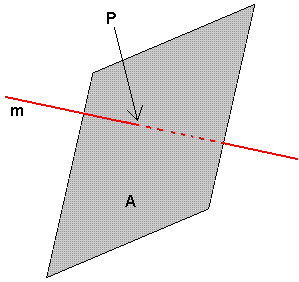
Skjæring mellom linje og plan

En rett linje kan ligge i planet. Da er alle punkter på linja også punkter i planet. En rett linje kan ligge paralellt med et plan, da har linjen og planet ingen punkter felles. En rett linje kan skjære et plan. Linjen og planet har da et felles punkt.

En linje er gitt som <tex> m: \left [ x = -1-k\\ y = 3+k \\ z = -k \right]</tex> og et plan er gitt som <tex> \alpha: \left [ x = x_0 + u_xs+v_xt\\ y = y_0 + u_ys+v_yt \\

z = z_0 + u_zs+v_zt \right]</tex>

---

Ligger punktet eller linja i planet?

PUNKT

Ligger punktet i planet? Dersom koordinatene til punktet passer i likningen for planet ligger punktet i planet, ellers ikke.

Et plan er gitt ved: 2x-3y+z-1=0. Ligger punktet S = (2, 1, 2) i planet?

Man setter inn for å se om punktets koordinater passer i likningen for planet. <tex> 2 \cdot 2 - 3\cdot 1 +2 -1 =0</tex>

LINJE

Dersom en linje ligger i planet er det nok å vise at to punkter på linjen ligger i planet

Et plan er gitt ved: 4x+5y+z-1 =0. Ligger linjen <tex> m: \left [ x = 1+4t\\ y = -1-3t \\ z = 2-t \right]</tex>

i planet?

Man velger et punkt på linja, t=0 gir (1, -1,2) som insatt i likningen for planet gir 4 + 5 + 2 - 1 = 0. Velger t=1 og får 20 - 20 + 1 -1 = 0. Linjen ligger i planet.