Pascals talltrekant

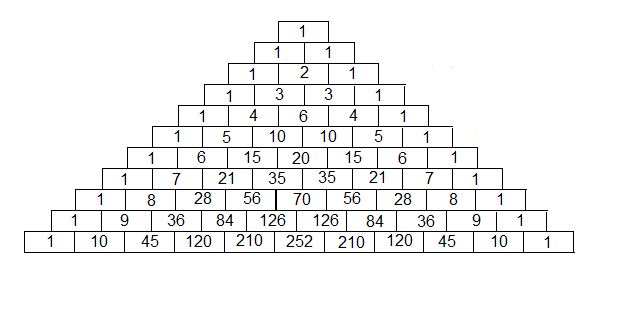
Pascalls talltrekant viser mange interesante sammenhenger. Vi ser på noen av dem her.

Hvordan bygge opp trekanten?

Tallet en står øverst, i NULLTE rad. Under kommer to enere i første rad, 1,2,1 i andre rad, osv. Langs sidene er det enere. Et tall i trekanten er summen av de to tallene på raden over. Tallene 10 på rad fem er summen 4+6 på rad fire, rett over.

Mønster i trekanten

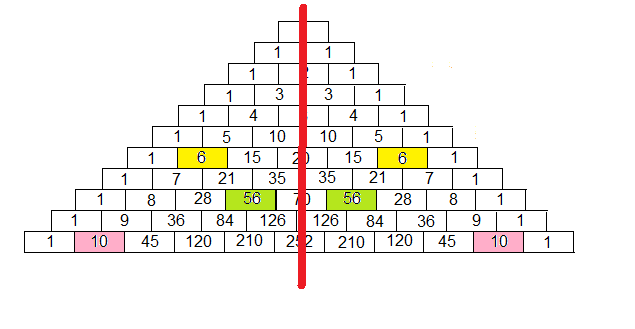
Symmetri

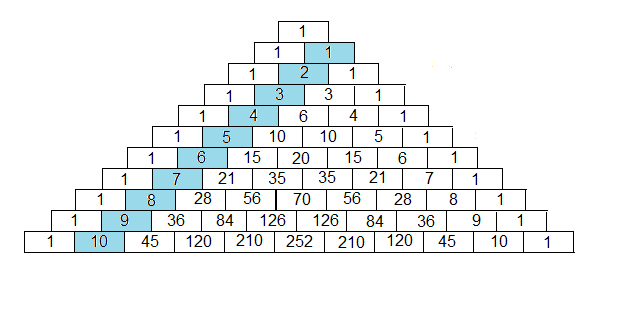
Naturlige tall

Horisontale summer

Dersom man summerer de horisontale radene i trekanten får man:

$1 = 2^0 \\ 1+1 =2 = 2^1 \\1+2+1=4 =2^2\\ 1+3+3+1 = 8 =2^3 \\ 1+4+6+4+1 = 16 =2^4 \\1+5+10+10+5+1 =32 = 2^5$

osv.

Man observerer at alle horisontale summer er potenser av to.

Polynomer

$ (x+1)^0 =$ 1

$ (x+1)^1 =$1 x+1

$(x+1)^2 =$ 1$x^2$+2x+1

$(x+1)^3$ = 1$x^3$+3$x^2$+3x+1

$(x+1)^4$ = 1$x^4$+4$x^3$+6$x^2$+4 x +1

Binominal koefisienter

$\dbinom{n}{k} \\ \dbinom{n}{k} \dbinom{n}{k} \\ \dbinom{n}{k} \dbinom{n}{k} \dbinom{n}{k} \\ \dbinom{n}{k} \dbinom{n}{k} \dbinom{n}{k} \dbinom{n}{k} \\dbinom{n}{k}dbinom{n}{k}dbinom{n}{k}dbinom{n}{k}dbinom{n}{k} $