Forskjell mellom versjoner av «Partiell derivasjon»
| (2 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 6: | Linje 6: | ||
$f(x,y) = 2xy^2 + 1$ | $f(x,y) = 2xy^2 + 1$ | ||
| − | Fra funksjoner med en variabel er vi kjent med at den deriverte i et punkt gi oss stigningstallet til tangenten i punktet. | + | [[ File:flervariabel.png ]] |
| + | |||
| + | Vi ser at funksjonen danner en flate med en krummning som varierer med x og y. | ||
| + | |||
| + | |||
| + | Fra funksjoner med en variabel er vi kjent med at den deriverte i et punkt gi oss stigningstallet til tangenten i punktet. Dersom vi har flere retninger ser vi på hver av hovedretningene for seg. Vi ser på den deriverte i x retning for seg selv, og den deriverte i y retning for seg. | ||
| + | |||
| + | Når vi deriverer med henyn på x behandler vi y som en konstant, og motsatt. | ||
| + | |||
| + | Deriverer vi $f(x,y) = 2xy^2 + 1$ med hensyn på x får vi: | ||
| + | |||
| + | $f'_x(x,y) = 2y^2$ | ||
| + | |||
| + | Deriverer vi med hensyn på y får vi: | ||
| + | |||
| + | $f ' _y (x,y)= 4xy$ | ||
Nåværende revisjon fra 4. feb. 2019 kl. 10:44
Funksjoner kan ha flere variabler. Dersom en funksjon har to variabler kan det skrives slik:
f(x,y), variablene her er x og y. Vi kan for eksempel ha en funksjon
$f(x,y) = 2xy^2 + 1$
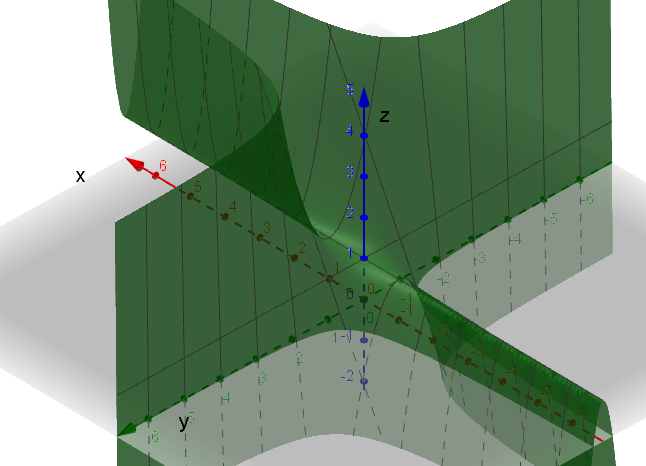
Vi ser at funksjonen danner en flate med en krummning som varierer med x og y.
Fra funksjoner med en variabel er vi kjent med at den deriverte i et punkt gi oss stigningstallet til tangenten i punktet. Dersom vi har flere retninger ser vi på hver av hovedretningene for seg. Vi ser på den deriverte i x retning for seg selv, og den deriverte i y retning for seg.
Når vi deriverer med henyn på x behandler vi y som en konstant, og motsatt.
Deriverer vi $f(x,y) = 2xy^2 + 1$ med hensyn på x får vi:
$f'_x(x,y) = 2y^2$
Deriverer vi med hensyn på y får vi:
$f ' _y (x,y)= 4xy$