Forskjell mellom versjoner av «Lineær optimering»
| Linje 11: | Linje 11: | ||
[[Bilde:opt1.PNG]] | [[Bilde:opt1.PNG]] | ||
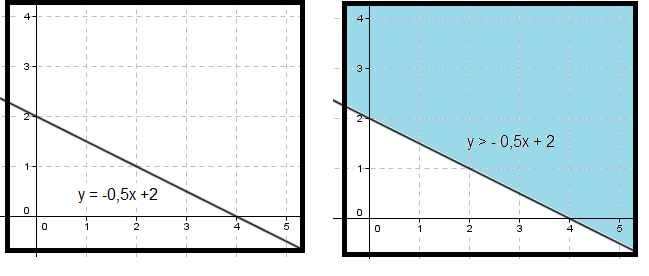
| − | Over ser man linjen y = - 0,5x + 2. Alle verdier større enn -0,5x + 2 er markert med blått, y > -0,5x+2. | + | Over ser man linjen $y = - 0,5x + 2$. Alle verdier større enn $-0,5x + 2$ er markert med blått, $y > -0,5x+2$. |
==Eksempel== | ==Eksempel== | ||
| Linje 22: | Linje 22: | ||
Overskuddet blir da: | Overskuddet blir da: | ||
| − | Z = 2x + 3y | + | $Z = 2x + 3y$ |
| − | Bedriften kalkulerer med at overskuddet skal bli nihundretusen. Dvs. z = 900000 | + | Bedriften kalkulerer med at overskuddet skal bli nihundretusen. Dvs. $z = 900000$ |
<math>900000 = 2x + 3y \\ y = - \frac 23x + 300000 </math> | <math>900000 = 2x + 3y \\ y = - \frac 23x + 300000 </math> | ||
Revisjonen fra 16. jun. 2013 kl. 08:16
Dette er en metode som kan brukes til å maksimere fortjenesten, ved å utnytte resursene eller innsatsfaktorene på en mest fornuftig måte. Resurser kan være
- Tid
- Arbeidskraft
- Kapital
- Råvarer
Man må være fortrolig med ulikheter og rette linjer i koordinatsystemet.
Over ser man linjen $y = - 0,5x + 2$. Alle verdier større enn $-0,5x + 2$ er markert med blått, $y > -0,5x+2$.
Eksempel
En bedrift lager og selger saftis og fløteis. Bedriften regner med at overskuddet blir 2 kroner per saftis og 3 kroner per fløteis. Vi setter
x = antall saftis
y = antall fløteis
Overskuddet blir da:
$Z = 2x + 3y$
Bedriften kalkulerer med at overskuddet skal bli nihundretusen. Dvs. $z = 900000$
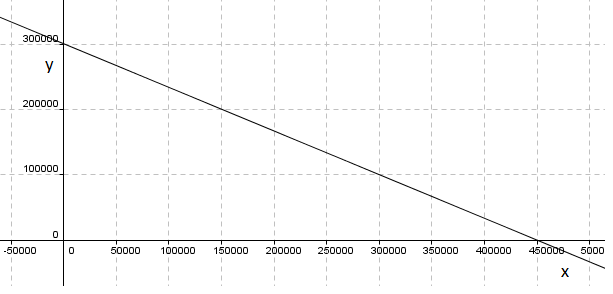
<math>900000 = 2x + 3y \\ y = - \frac 23x + 300000 </math>
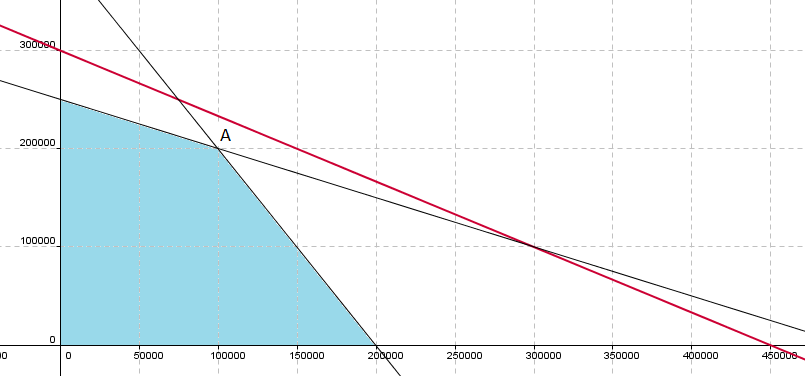
Alle kombinasjoner av punkter på linjen vil gi et overskudd på 900000 kr. Dersom det ikke er noen begrensninger på resurser kan jo bedriften velge antall av iskremtyper selv. Slik er det normalt ikke.