Introduksjon til differensiallikninger

Innledning

En differensialligning vil typisk beskrive en forandring av en variabel i tid og/eller rom. Den skiller seg fra "vanlige" ligninger ved at løsningene er funksjoner, ikke bestemte verdier. Teorien for differensialligninger er fundamental for forståelsen av dynamikken i naturen og danner grunnlaget for blant annet klassisk mekanikk og kvantemekanikk. Vi deler diff.ligningene inn i partielle og ordinære ligninger, der matematikken i videregående skole kun fokuserer på ordinære ligninger, ofte kalt ODE (Ordinary Differential Equations). Dvs. at løsningsfunksjonen kun har én variabel, som oftest kalt $t$ (for tid) eller $x$ (for rom). Det er vilkårlig hvilken notasjon vi bruker så lenge vi er bevisst på hva som er den ukjente funksjonen og hva som er variabelen.

På ungdomstrinnet og videregående grunnkurs arbeidet man med ligninger der den ukjente var et tall, ofte kalt $x$.
I differensialligninger er den ukjente en funksjon $y(x)$. En differensialligning gir sammenhengen mellom en ukjent funksjon og noen av dens deriverte.
I denne artikkelen skriver vi <math>y^\prime</math> og <math> \frac{dy}{dx}</math> om hverandre. Den siste skrivemåten kalles Leibniz' notasjon etter den tyske filosofen og matematikeren Gottfried Wilhelm Leibniz.
Man bør være fortrolig med ligninger, funksjonslære, integrasjon og derivasjon før man gir seg i kast med differensialligninger.
Ligningene er viktige i fysikk og andre fag, der de kan brukes til å modellere forskjellige fysiske situasjoner.

Ordenen til en diff.ligning

Formelt vil en ordinær diff.ligning være på formen <math>g(x,f,f^\prime ,f^{\prime \prime},\ldots , f^{(n)})=0</math> der <math>g</math> er en gitt funksjon. <math>n</math> kalles ligningens orden og <math>f^{(n)}</math> er den n-te deriverte. <math>f</math> er her den ukjente funksjonen som vi ønsker å finne, og <math>x</math> er variabelen som vi deriverer med hensyn på, dvs. <math>f^\prime \equiv \frac{df}{dx}</math>, <math>f^{\prime \prime} \equiv \frac{d^2f}{dx^2}</math>, etc.

Eksempel på diff.ligning av første orden

En enkel ordinær differensialligning av første orden er <math>f^{\prime}(x)=0</math>. Løsningen finnes direkte ved integrasjon; vi får at <math>f(x)=c</math> for en konstant <math>c</math>.

Eksempel på diff.ligning av 2.orden

En enkel andreordens ordinær differensialligning er <math>m\ddot{x}(t)=10</math>. Dette er Newtons andre lov med konstant kraft (10 N) der <math>x(t)</math> er posisionen ved tida <math>t</math>. De to prikkene over <math>x</math> betyr at vi dobbeltderiverer <math>x</math> med hensyn på tiden.

Førsteordens lineære ligninger

Lineære differensialligninger av første orden kan skrives på formen

\begin{equation} \label{linearEqFirstOrder} y' + ay = b \end{equation}

At en likning er av første orden betyr at den inneholder den førstederiverte, $y'$, men ikke deriverte av høyere orden ($y^{\prime\prime}$, $y^{(3)}$ etc.).

Homogene og inhomogene førsteordens diff.ligninger

Dersom $b\neq 0 $ i ligning \ref{linearEqFirstOrder} kalles den inhomogen. Dersom $b = 0$ kalles diff.ligningen homogen. En homogen, lineær diff.ligning av første orden er altså på formen

\begin{equation} \label{linearHomEqFirstOrder} y' + ay = 0 \end{equation}

Slike ligninger kan løses på to måter:

Multiplikasjon med integrerende faktor
Som en separabel ligning

Løsningsmetoder er illustrert i følgende eksempler:

Eksempel: Homogen ligning, integrerende faktor

Vi skal løse $y'+2y = 0$. Integrerende faktor er $e^{2x}$.
\begin{align*} y'+2y & = 0 \\ e^{2x}y'+2e^{2x}y & = 0 \quad \text{Multiplisert med integrerende faktor}\\ (e^{2x}y)' & = 0 \\ e^{2x}y & = C \\ y & = Ce^{-2x} \end{align*}
For å finne ut hva $C$ er trenger man i tillegg en initialbetingelse (startbetingelse) på løsningen. Det behandles i avsnittet om Initialverdiproblemer.

Eksempel: Inhomogen ligning, integrerende faktor

Vi skal løse $y'+4y = 6$. Integrerende faktor er $e^{4x}$.
\begin{align*} y'+4y & = 6 \\ e^{4x}y'+4e^{4x}y & = 6e^{4x} \quad \text{Multiplisert med integrerende faktor}\\ (e^{4x}y)' & = 6e^{4x} \\ e^{4x}y & = \int 6e^{4x}\,dx\\ e^{4x}y & = \frac{3}{2}e^{4x}+C\\ y & = \frac{3}{2}+Ce^{-4x} \end{align*}
For å finne ut hva $C$ er trenger man i tillegg en initialbetingelse (startbetingelse) på løsningen.

Separable ligninger

Separable ligner er ligninger på formen:

Ligningen løses ved å multiplisere med dx på begge sider av likhetstegnet, for så i integrere:

<math>\frac{dy}{h(y)} = g(x)dx \\

Setter \frac{1}{h(y)} = f(x)</math>

og får:

Eksempel 4

Løs ligningen:

<math> \frac{dy}{dx} =-4xy \\ \frac{dy}{y} =-4xdx \\ \int{\frac{dy}{y}} =\int{-4xdx} \\ ln|y| = -2x^2 + C \\ y = e^{-2x^2 + C} \\ y = e^C \cdot e^{-2x^2} </math>

Homogene lineære andreordens differensialligninger med konstante koeffisienter.

Vi har likningen

<math>A(x)y^{} + B(x)y' + C(x)y = D(x)</math>

En ligning er homogen når D(x) = 0. Det gir oss

<math>A(x)y^{} + B(x)y' + C(x)y = 0</math>

Konstante koeffisienter betyr at A(x), B(x) og C(x) ikke er variabler men konstanter. Vi skriver ligningen på formen:

<math>y^{} + by' + cy = 0</math>

En eventuell konstant foran den dobbelderiverte fjernes med divisjon.

Andreordens betyr at den dobbelderiverte opptrer i ligningen. I en tredjeorden ligning vil den tredjederiverte opptre.

Lineær betyr at produkter eller potenser av y og dens deriverte ikke eksisterer i ligningen. ( y = yy' er således et eksempel på en ikkelineær ligning.)

(1) y + by' + cy = 0

Ligningen

r² + br + c = 0

kalles den karakteristiske ligningen til differensialligningen i (1).

Dette gir tre mulige løsninger:

To reelle røtter
En reel rot
To komplekse røtter

Dersom ligningen har to reelle røtter gir det generell løsning

<math>y(x) = C_1e^{r_1x} + C_2e^{r_2x}</math>

Eks. 5:

<math> y^{,,} + y^{,} = 2y \\ y^{,,} + y^{,} - 2y = 0 \\ r^2 + r - 2 = 0 \\ r = 1 \wedge r = 2 \\ y(x) = C_1e^x + C_2e^{2x}</math>

Test deg selv

Dersom ligningen har en reel rot blir løsningen på formen
<math>y(x) = C_1e^{rx} + C_2xe^{rx}</math>

Eks. 6:
<math>4y^{,,} + 8y^{,} + 4y =0 \\r^2 + 2r + 1 = 0 \\r = -1\\y(x) = C_1e^{-x} + C_2xe^{-x}</math>

Test deg selv

Dersom ligningen har to koplekse røtter,<math>r_1 = a + ib og r_2 = a - ib</math> blir løsningen
<math>y(x) = e^{ax}(C_1 cos(bx) + C_2 sin (bx))</math>

Eks. 7:

<math>y^{,,}-y^, + y = 0 \\ r^2 - r + 1= 0 \\ r_1 = \frac12 + \frac32i r_2 = \frac12 - \frac32i')\\ y(x) = e^{\frac12x}(C_1 cos(\frac32x) + C_2 sin (\frac32x))</math>

Test deg selv

Initialverdiproblemer

I eksemplene over (og senere) ser man at den generelle løsningen inneholder en eller to konstanter C₁ og C₂. Disse kan i utgangspunktet være et hvilket som helst reelt tall. For å finne den spesielle løsningen til en ligning trenger man en eller flere tileggsopplysninger.

Når en differensialligning er gitt med initialbetingelser kalles det for et initialverdiproblem.

Initialbetingelsen(e) kan være knyttet til situasjonen ved tiden t = 0, altså når en prosess starter, eller den kan gis i form av en funksjonsverdi for en annen argumentverdi.

Eks 8:

Finn den spesielle løsningen til initialverdiproblemet:

<math>\frac{dy}{dx} = 3x + 2 \hspace{50 mm} y (1)= 3 \\ dy = (3x + 2)dx \\ y(x) = \int (3x + 2)dx \\ y(x) = \frac 32x^2 + 2x + c </math>
Dette er den generelle løsningen.

For å finne den spesielle løsningen benytter vi opplysningen
y(1) = 3.

<math>y(1) = \frac 32 \cdot 1^2 + 2 \cdot 1 + c = 3 \\ C = - \frac 12 </math>
Den spesielle løsningen blir:

<math>y(x) = \frac 32 \cdot x^2 + 2 x - \frac 12 </math>

Retningsdiagram

Førsteorden ligninger kan skrives som y'(x) = F(x,y) der x er den variable og y er den ukjente

funksjonen. Dette gir stigningstallet til tangen i punktet (x,y). Dette gir et bilde av hvordan grafene til løsningsfunksjonene ser ut og kalles et retningsdiagram for differensialligningen.

På engelske er betegnelsen "slope field".

Eks 9:

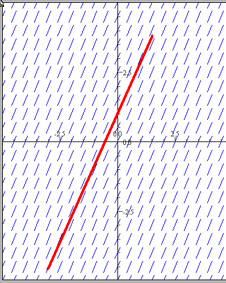
Gitt er ligningen y' = 2

Man observerer at stigningstallet til y(x) er 2 for alle x. Løsningen på ligningen er en eller
annen rett linje med stigningstall 2. Et retningsdiagram illustrerer dette:

Dersom man løser ligningen y' = 2

Får man y = 2x + C, når man integrerer på begge sider.

Man ser nå at retningsdiagrammet stemmer, C skyver grafen opp eller ned i koordinatsystemet. Verken x eller y har noen betydning for grafens form. Diagrammet indikerer en løsning for y = 2x + 1

Eks 10

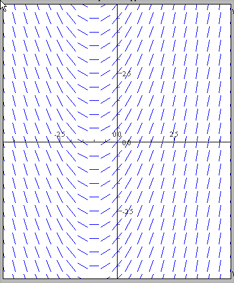
Gitt er ligningen y' = x + 1

Man observerer at stigningstallet til y(x) varierer med varierende x verdi, og er null for x = -1. Det gir følgende retningsdiagram:

Dersom man løser ligningen y' = x + 1
Får man
<math> y = \frac 12x^2 + x + c </math>
når man integrerer på begge sider.

Retningsdiagrammet indikerer at løsningen er en parabel med minimum i x = -1

Tilbake til R2 Hovedside