Forskjell mellom versjoner av «GeoGebra - introduksjon til å løse likning grafisk»
Fra Matematikk.net
(Ny side: Jeg skal nå finne ut når $y$-verdien blir lik 1.5. For å gjøre dette, skriver jeg inn dette: File:geogebraintro-pasted8.png Resultatet blir en rett linje: [[File:geogebraintro...) |
|||
| Linje 32: | Linje 32: | ||
Her kan jeg se at $x$-verdien til punktet er 2.5 (1.5 er $y$-verdien | Her kan jeg se at $x$-verdien til punktet er 2.5 (1.5 er $y$-verdien | ||
| − | som vi visste fra før) - da har jeg løst likningen grafisk: | + | som vi visste fra før) - da har jeg løst likningen grafisk: $x=2.5$ |
| − | |||
| − | |||
| − | x=2.5 | ||
| − | |||
Revisjonen fra 24. mar. 2014 kl. 21:09
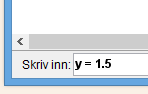
Jeg skal nå finne ut når $y$-verdien blir lik 1.5. For å gjøre dette, skriver jeg inn dette:
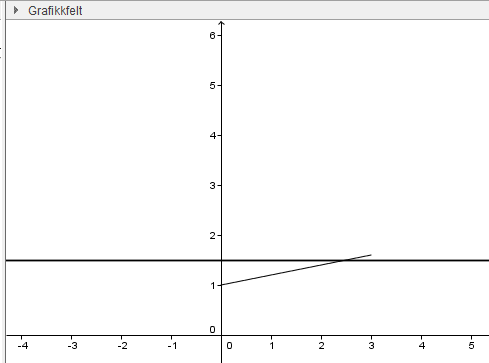
Resultatet blir en rett linje:
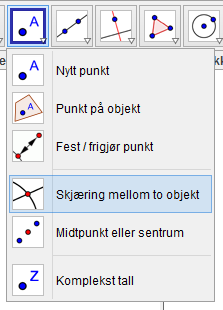
For å løse likningen grafisk, er det $x$-verdien i skjæringspunktet jeg er ute etter. Jeg går opp i menyen og trykker på denne knappen:
I menyen som kommer fram, velger jeg Skjæring mellom to objekt:
Etter å ha trykket på denne knappen
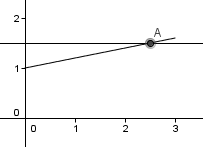
trykker jeg først på grafen og så på den rette linjen. Da skal skjæringspunktet komme fram:
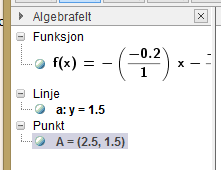
For å finne $x$-verdien til skjæringspunktet, ser jeg i algebrafeltet på punktet A:
Her kan jeg se at $x$-verdien til punktet er 2.5 (1.5 er $y$-verdien som vi visste fra før) - da har jeg løst likningen grafisk: $x=2.5$