Forskjell mellom versjoner av «Funksjoner»
| (185 mellomliggende revisjoner av 2 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
| − | Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for akser. Punktet der aksene krysser hverandre kalles for origo. Den vannrette aksen kalles for x- aksen eller første aksen. Den loddrette aksen kalles for y- aksen eller andre aksen. | + | Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for akser. Punktet der aksene krysser hverandre kalles for origo.Begge aksene har verdien null i origo. Den vannrette aksen kalles for x- aksen eller første aksen. Den loddrette aksen kalles for y- aksen eller andre aksen. |
| − | Et punkt kan bestemmes med to tall ( et tallpar ) som vi kaller koordinater. Tallpar skrives på formen (x,y). Origo har koordinatene (0, 0). Man oppgir alltid x verdien først . Punktet (1,3) har verdiene x = 1 og y = 3. Her er eksempler på noen punkter: A (1,2), B (4,0), C (-1, -2), D (-2, 0). | + | Et punkt kan bestemmes med to tall ( et tallpar ) som vi kaller koordinater. Tallpar skrives på formen (x,y). Origo har koordinatene (0, 0). Man oppgir alltid x verdien først . Punktet (1,3) har verdiene x = 1 og y = 3. |
| + | |||
| + | [[Bilde:Figen.png]] | ||
| + | |||
| + | Her er eksempler på noen punkter: A (1,2), B (4,0), C (-1, -2), D (-2, 0). | ||
| − | [[ | + | På denne måten kan alle ”steder” (punkter) i et plan representeres, med en x koordinat og en y koordinat. Alle [[kart]] er laget på denne måten. X – aksen er da øst - vest retning og Y – aksen er nord – sør retningen.<br> |
| + | [http://www.matematikk.net/emner/applets/ggbApplet.php?appid=7 Lek med koordinatsystemet] | ||
| + | |||
| + | |||
| + | |||
| + | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85A%2B85B%2B85C%2B85D%2B85E%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
| − | |||
== Funksjon == | == Funksjon == | ||
| Linje 31: | Linje 39: | ||
<br> | <br> | ||
Hva gjør boksen? | Hva gjør boksen? | ||
| − | Den legger til to til det tallet som blir stappet inn i boksen. Vi kallet boksen for | + | Den legger til to til det tallet som blir stappet inn i boksen. Vi kallet boksen for y? La oss kalle tallet vi putter inn for x. |
Vi kan skrive dette slik matematisk: | Vi kan skrive dette slik matematisk: | ||
| − | + | $$y = x + 2$$ | |
| − | + | $y = x + 2$ kalles for funksjonsutrykket. | |
| − | Vi sier at | + | Vi sier at y er en funksjon av x. Verdien av y avhenger av verdien av x. Detter er det vi kaller en lineær funksjon, dvs. en rett linje. |
=== Funksjonssuttrykk === | === Funksjonssuttrykk === | ||
| − | Funksjonen f(x) = 2x + 5 har funksjonsuttrykket 2x + 5. Uttrykket forteller hva som skal gjøres med tallet som skal inn i funksjonen. I dette tilfellet skal tallet multipliseres med 2 og 5 legges til. | + | Funksjonen $f(x) = 2x + 5$ har funksjonsuttrykket $2x + 5$. Uttrykket forteller hva som skal gjøres med tallet som skal inn i funksjonen. I dette tilfellet skal tallet multipliseres med 2 og 5 legges til. |
| + | $f$ er navnet på funksjonen. Bokstaven i parantes er navnet på den variable. Vanlige navn er $x$ og $t$. $t$ brukes gjerne om tid. Vanlige funksjonsnavn er $f,g,h$ og $V$, for å nevne noen. Man kan gi en funksjon det navn man ønsker, men det er fornuftig å gi navn som forteller noe om hva funksjonen gjør. | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | ||
| + | :[https://youtu.be/yCQjRFkbZRw '''Video eksempel:''' Hva er en funksjon?] | ||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | ||
| + | :[https://youtu.be/ySnXylD78II '''Video eksempel:''' Hvordan lage funksjoner ut fra praktiske situasjoner.] | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85A%2B85B%2B85C%2B85D%2B85E%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
=== Graf === | === Graf === | ||
| Linje 53: | Linje 74: | ||
| − | Det er viktig å legge merke til at dersom kurven representerer en funksjon finnes det bare en | + | Det er viktig å legge merke til at dersom kurven representerer en funksjon finnes det bare en y-verdi for hver x-verdi. For en y-verdi kan det finnes flere x-verdier. Dersom x er forskjellige tidspunkt på dagen og y er temperaturen, betyr det at et tidspunkt kan kun ha en temperatur, men en temperatur kan ha forekommet flere tider på dagen. |
| − | [[Bilde:Figto.png]] | + | [[Bilde:Figto.png]] |
| + | |||
| + | ''Figuren viser hvordan en tilfeldig x verdi kun kan ha en tilhørende y verdi, mens en tilfeldig y verdi kan ha to eller flere tilhørende x verdier.'' | ||
| + | |||
| + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | ||
| + | :[https://youtu.be/bRcJQsATAnM '''Video eksempel:''' Fra funksjonsuttrykk, via verditabell, til graf] | ||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85A%2B85B%2B85C%2B85D%2B85E%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
=== Definisjonsmengde === | === Definisjonsmengde === | ||
| − | Hvilke verdi den variable kan ha i funksjonen bestemmes av definisjonsmengden D. Dersom funksjonens navn er f, brukes notasjonen < | + | Hvilke verdi den variable kan ha i funksjonen bestemmes av definisjonsmengden D. Dersom funksjonens navn er f, brukes notasjonen <math>D_f = [x_1, x_2]</math>. Alternativt bruker man <math> x \in [x_1, x_2] </math> |
=== Verdimengde === | === Verdimengde === | ||
| − | Hvilke verdier som kommer ut av funksjonen, funksjonsverdiene, er bestemt av definisjonsmengden og av funksjonsuttrykket, Mengden av funksjonsverdier verdiene kalles Verdimengden. Om funksjonens navn er f brukes notasjonen | + | Hvilke verdier som kommer ut av funksjonen, funksjonsverdiene, er bestemt av definisjonsmengden og av funksjonsuttrykket, Mengden av funksjonsverdier verdiene kalles Verdimengden. Om funksjonens navn er f brukes notasjonen <math> V_f </math>. |
Man kan se på en funksjon som en ”bro” mellom mengder, definisjonsmengden og verdimengden. | Man kan se på en funksjon som en ”bro” mellom mengder, definisjonsmengden og verdimengden. | ||
| Linje 72: | Linje 103: | ||
[[Bilde:Graf.png]] | [[Bilde:Graf.png]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |
| + | :[https://youtu.be/XFgEyYxmRs8 '''Video eksempel:''' Fra Definisjonsmengde til verdimengde.] | ||
| + | </div> | ||
| − | |||
| − | |||
| − | + | [http://www.matematikk.net/emner/applets/ggbApplet.php?appid=8 Lek med verdi og definisjonsmengde] | |
| + | === Sentrale Punkter på grafen=== | ||
| + | ====Nullpunkter==== | ||
| − | + | Et nullpunkt er et sted der grafen til en funksjon kysser x -aksen. Dersom vi har funksjonen f(x) finner vi eventuelle nullpunkter ved å løse likningen f(x) = 0. En funksjon kan ha ingen, ett eller flere nullpunkter avhengig av type funksjon, definisjonsområde og koeffisienter. Visuelt finner man nullpunktene ved å lese av verdien på x-aksen, der grafen krysser aksen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |
| + | :[https://youtu.be/4I4R5EK2JoA '''Video eksempel:''' Nullpunkter og skjæring med y-aksen.] | ||
| + | </div> | ||
| − | + | ==== Skjæring med y- akse==== | |
| − | + | f(0) gir skjæring med y- akse. Vi kaller ofte denne verdien konstantleddet. Et interessant punkt når man skal tegne grafen til funksjonen. Vil være startvedien til funksjonen dersom den er definert for x verdier fra og med null og oppover, $x \in[ 0, \rightarrow>$. | |
| − | + | == Funksjonstyper == | |
| − | |||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |
| − | + | :[https://youtu.be/TPfGIZ-q6fY '''Video eksempel:''' Hvordan skrive funksjoner i Geogebra.] | |
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| + | ===Lineære funksjoner=== | ||
| − | + | Det at en funksjon er lineær betyr at om vi tegner grafen i et koordinat system med X verdier på førsteaksen og Y verdier på andreaksen får vi en rett linje. Det generelle funksjonsuttrykket er: | |
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |
| + | $ y = ax + b $ eller $f(x) = ax+b$ som betyr det samme og er en mer vanlig skrivemåte. | ||
| + | </div> | ||
| − | + | a kalles for stigningstallet og b for konstantleddet. Dersom x er null er Y lik b. Konstantleddet b forteller hvor grafen krysser y-aksen. a forteller hvor mange enheter man beveger seg i y rettning (opp eller ned), når man beveger seg en enhet til høyre på x aksen. | |
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |
| − | + | Dersom a er positiv betyr det at grafen stiger mot høyre, med økende x verdi. Desto høyere a verdi, desto brattere stiger grafen. | |
| − | + | <p></p> | |
| − | + | Dersom a er negativ betyr det at Y avtar mot høyre, eller med økende X verdi. | |
| − | + | <p></p> | |
| − | + | Tallet b forteller hvor grafen krysser Y aksen. Når grafen krysser Y aksen er X verdien lik null. | |
| − | + | </div> | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| + | '''Eksempel 1:'''<br> | ||
| − | = | + | Vi har funksjonsuttrykket: |
| + | <math> y = \frac12x + 2 </math> <br> Grafen ser slik ut:<br> [[Bilde:linje.PNG]] <br> | ||
| + | Man observerer at grafen går gjennom punktet (0,2) på y aksen. Stigningstallet er <math>\frac12</math>. Det betyr at når man beveger seg en enhet til høyre må man bevege seg 0,5 (en halv) oppover i y rettning for å treffe grafen igjen. | ||
| + | </div> | ||
| − | |||
| − | |||
| − | + | [http://www.matematikk.net/emner/applets/ggbApplet.php?appid=11 Lek med rette linjer] | |
| − | |||
| − | |||
| − | |||
| − | + | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85A%2B85B%2B85C%2B85D%2B85E%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |
| − | + | Dersom man har kontroll på stigningstall og konstantledd er det greit å tegne grafen med bare disse to størrelsene. Dersom man synes dette er vannskelig er det lurt å lage en verditabell. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==== Verditabell ==== | |
| − | |||
| − | |||
| − | |||
| − | + | Vi velger selv tilfeldige X verdier. Det er gjerne lurt å velge verdier som ligger nærheten av origo. | |
| + | <p></p> | ||
| + | Når vi har valgt en X verdi setter vi den inn for X i funksjonstrykket (1). Da får vi en Y verdi som hører til X verdien. | ||
| + | <p></p> | ||
| + | Disse resultatene setter vi inn i en tabell. Ut i fra disse verdiene tegner vi grafen. I vårt eksempel kan verditabellen se slik ut: | ||
| − | < | + | <p></p> |
| + | Verditabell er en samling av punkter på grafen, altså sammhørende verdier av x og f(x). Formålet med å lage en verditabell er at du har nok punkter til å kunne tegn eller skissere grafen. | ||
| − | + | Det anbefales at du lærer deg å bruke kalkulatoren når du skal lage verditabeller. | |
| − | |||
| − | + | Av og til er det imidlertid nødvendig å kunne lage tabellen manuelt. Det gjøres ved at du selv velger et antall x verdier i det området du skal tegne grafen. Du setter inn x verdiene i funksjonsuttrykket og finner sammhørende funksjonsverdier. Hvor mange verdier du velger kommer an på hvor nøyaktig du ønsker det. Flere verdier gir økt nøyaktighet. | |
| − | |||
| − | = | + | <br> |
| + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| − | + | '''Eksempel 2:''' <br><br> | |
| − | + | Vi ønsker å tegne grafen til f(x) = 2x -3 i området fra x = -2 til x = 2. | |
| − | + | <br><br>Vi velger x lik -2, -1, 0, 1, 2 og får:<br> | |
| − | |||
| − | + | <table border="1" cellpadding="10"> | |
| − | |||
| − | + | <tr> | |
| + | <td> x <br></td> | ||
| + | <td> f(x)= 2x - 3 </td> | ||
| + | <td> f(x) </td> | ||
| + | <td>(x, f(x))</td> | ||
| − | + | </tr> | |
| + | <tr> | ||
| + | <td> -2</td> | ||
| + | <td> f(-2) = 2 (-2) - 3 </td> | ||
| + | <td> f(-2)= -7</td> | ||
| + | <td> (-2, -7)</td> | ||
| − | + | </tr> | |
| + | <tr> | ||
| + | <td>-1 </td> | ||
| + | <td> f(-1) = 2 (-1) – 3</td> | ||
| + | <td> f(-1) = -5</td> | ||
| + | <td> (-1,-5) </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td> 0 </td> | ||
| + | <td> f(0) = 2 (0) – 3</td> | ||
| + | <td> f(0)= -3</td> | ||
| + | <td> (0, -3)</td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td> 1</td> | ||
| + | <td> f(1) = 2 (1)– 3</td> | ||
| + | <td> f(1)= - 1</td> | ||
| + | <td> (1, -1) </td> | ||
| − | + | </tr> | |
| + | <tr> | ||
| + | <td> 2 </td> | ||
| + | <td> f(2) = 2 (2) – 3</td> | ||
| + | <td> f(2) = 1</td> | ||
| + | <td> (2, 1) </td> | ||
| − | + | </tr> | |
| − | + | </table> | |
| − | |||
| − | |||
| + | Og grafen ser slik ut: | ||
| − | + | [[Bilde:linje2.PNG]] | |
| + | </div> | ||
| − | + | ====Ettpunktsformelen==== | |
| − | + | Dersom du kjenner et punkt på linjen og stigningstallet kan du finne funksjonsutrykket ved å bruke følgende formel:<br> | |
| + | <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> y-y_1 = a(x-x_1) </math> | ||
| + | <p></p> | ||
| + | a er stigningstallet og <math>(x_1 , y_1) </math> er koordinatene til punktet. | ||
| + | <p></p> | ||
| + | </div> | ||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |
| − | + | '''Eksempel 3:''' | |
| − | + | Hva er funksjonsuttrykket til en funksjon som har stigningstall 2 og går gjennom punktet (-2,-1)? | |
| − | + | <p></p> | |
| + | <math> y-(-1) = 2(x-(-2)) </math> | ||
| + | <p></p> | ||
| + | <math> y = 2x + 3 </math> | ||
| + | <p></p> | ||
| + | </div> | ||
| − | + | ||
| − | |||
| + | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85A%2B85B%2B85C%2B85D%2B85E%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
| + | ====Topunktsformelen==== | ||
| − | + | Dersom man kjenner to punkter på en rett linje er stigningstallet a gitt som: | |
| + | <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> a =\frac{\Delta y}{\Delta x}=\frac{y_2 - y_1}{x_2 - x_1} </math> | ||
| + | <p></p>Desom man setter dette uttrykket inn i etpunktsformelen over får man:<p></p> | ||
| + | <math> y- y_1=\frac{y_2 - y_1}{x_2 - x_1}(x-x_1) </math> | ||
| − | |||
| − | |||
| − | + | <p></p> | |
| + | </div> | ||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |
| + | '''Eksempel 4:''' | ||
| + | En lineær funksjon gpr gjennom punktene (1,4) og (3,5). Finn funksjonsuttrykket. | ||
| + | </div> | ||
| + | ===Andregradsfunksjoner=== | ||
| + | Funksjonsuttrykket til en andregradsfunksjon er gitt som <br> | ||
| + | <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> f(x) = ax^2 + bx + c </math> | ||
| + | </div> | ||
| − | + | Gitt på denne formen er <math>ax^2</math> andregradsleddet, bx er førstegradsleddet og c er konstantleddet. Grafene til andregradsfunksjoner kalles parabler. Grafene krummer og er symmetriske om symmetriaksen som er gitt som: | |
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | '''Symmetriakse:'''<br> | ||
| + | <math> x = \frac{-b}{2a}</math> | ||
| + | </div> | ||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |
| + | '''Eksempel 5:'''<br><br> | ||
| + | Finn symmetriaksen til funksjonen<br> <math> f(x) = -x^2 + 2x + 4 </math><br><br> | ||
| + | '''Løsning:'''<br><br> | ||
| + | <math> x = \frac{-b}{2a} =\frac{-2}{2 \cdot (-1)} =1</math> | ||
| + | </div> | ||
| − | |||
| + | Dersom konstanten a i andregradsleddet er positiv vender grafen sin hule side oppover, den ”smiler” | ||
| + | Dersom konstanten er negativ vender grafen sin hule side nedover, den er ”sur”. | ||
| − | + | En andregradsfunksjon kan også være gitt på formen | |
| + | <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> f(x) = a(x + b)^2 + c </math> | ||
| + | </div> | ||
| + | |||
| + | Konstanten a vil være den samme i begge fremstillingsmåter, men konstantene b og c er forskjellige. Hvilke fremstillingsmåte man benytter er smak og behag, men begge har sine fordeler. | ||
| − | |||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |
| + | '''Eksempel 6:''' <br><br> | ||
| + | <math>f(x) = a(x + b)^2 + c </math> | ||
| + | </div> | ||
| − | |||
| − | + | Grafen nedenfor viser funksjonen | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | I f(x) = 0,4x2 -2x +1 | |
| + | eventuelt | ||
| − | + | II f(x) = 0,4(x -2,5)2 -1,5 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Fordelen med utrykk I er at det er på formen man bruker i ”abc” formelen, for å finne nullpunkter. | |
| + | Fordelen med uttrykk II er at det gir symmetriakse og minimumspunkt direkte. Dersom man multipliserer ut parentesene og trekker sammen ender man opp med uttrykk I. | ||
| − | + | [http://www.matematikk.net/emner/applets/ggbApplet.php?appid=9 Animasjon] | |
| − | + | ===Rasjonale funksjoner=== | |
| + | Funksjoner der x inngår som en del av nevneren kalles brøkfunksjoner eller asymptotiske funksjoner. . Funksjonene går ofte mot en grense når x går mot en bestemt verdi. Dette kalles for asymptoter. | ||
| − | + | En rett linje som grafen til f(x) nærmer seg når x går mot en bestemt verdi eller <math> \pm \infty </math>. En graf kan godt krysse en asymptote. Vi har vertikale og horisontale (eller skrå) asymptoter. | |
| + | |||
| + | [[Bilde:hvass.PNG]] | ||
| + | Figuren viser grafen til funksjonen <math>f(x)= \frac{x-1}{x-2}</math> | ||
| + | Vi ser at grafen har en vertikal asymptote for x = 2 og en horisontal asymptote for y = 1. | ||
| − | + | ==== Vertikal asymptote ==== | |
| + | Dersom f (x) går mot pluss / minus uendelig når x nærmer seg et tall a fra den ene eller andre siden (eller begge) så er linjen X = a en vertikal asymptote for f. Dette kan formuleres slik: | ||
| + | |||
| + | <math> \lim\limits_{x \to a^+} f(x)= \pm \infty \quad \quad \quad \lim\limits_{x \to a^-} f(x)= \pm \infty </math><p></p> | ||
| + | I eksempelet over er a = 2. | ||
| − | + | ==== Horisontal (og skrå) asymptote ==== | |
| − | + | For å finne den horisontale asymptoten må vi undersøke hva som skjer med verdien av f (x) når x går mot ± uendelig. Dette skrives slik: | |
| + | <math> \lim\limits_{x \to \infty} f(x)= k \quad \quad \quad \lim\limits_{x \to - \infty} f(x)= k </math><p></p> | ||
| − | + | Dette leses "grenseverdien til f (x) når x går mot pluss / minus uendelig". Dersom et eller begge kriteriene er oppfylt er linjen y = k en horisontal asymptote for f. | |
| + | For å kunne se hva f går mot når x går mot ± uendelig kan det være nødvendig å foreta en polynomdivisjon. Dersom <math>f(x)= \frac{h(x)}{g(x)} </math> utfører vi divisjonen. Dersom vi gjør det med eksempelet over ser vi at f (x) kan skrives som <math>f (x) = 1+ \frac{1}{x-2}</math>. Nå ser vi lett at f går mot 1 når x går mot ± uendelig. | ||
| + | Når teller og nevner er av samme orden blir asymptoten en horisontal linje. Dersom telleren h (x) er en orden over nevneren får vi en skrå asymptote. Dersom vi har funksjonen <math>f (x)= \frac{3x^2 + 2x -5}{x} </math>og utfører divisjonen ser vi at den kan skrives som <math>f (x)= 3x + 2 - \frac 5x</math>. Vi ser at når x går mot ± uendelig går f mot den rette linjen 3x + 2. Grafen ser slik ut: | ||
| + | |||
| + | [[Bilde:Skra.PNG]] | ||
| − | |||
| + | ---- | ||
| + | [[Kategori:lex]] | ||
| + | ===Polynomfunksjoner=== | ||
| − | + | Funksjoner som består av flere ledd. Både rettlinjede funksjoner og andregradsfunksjoner er polynomfunksjoner, men så sentrale at de behandles spesielt. | |
| − | + | Generelt er polynomfunksjoner gitt ved: | |
| + | <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> f(x) = a\cdot x^n + b\cdot x^{n-1}+ ...+ c </math><br> | ||
| − | + | </div><br> | |
| − | |||
| − | |||
| + | <br> | ||
| + | Der n er hele positive tall. | ||
| − | |||
| − | |||
| − | + | På vgs. befatter vi oss av og til med funksjoner av 3. og 4. grad, men sjelden funksjoner av høyere grad. | |
| + | === Potensfunksjoner === | ||
| + | Potensfunksjoenr er av typen: | ||
| − | + | <br> | |
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math>f(x) = a\cdot x^b </math><br> | ||
| + | der x og b >0 | ||
| + | </div><br> | ||
| − | + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |
| + | '''Eksempel:'''<br> | ||
| + | $ f(x) = a\cdot b^x$ | ||
| + | </div><br> | ||
| − | + | (Dersom b = -1 har vi en asymptotisk funksjon hvis graf er en hyperbel. Dersom b = 1 får man en rett linje gjennom origo, med stigning en. Legg merke til at f(1) = a, fordi 1b er 1 uansett b - verdi.) | |
| − | + | Dersom 1>b>0 vokser funksjonen raskest for små verdier av x, for så å avta noe (avhengig av b). Dersom b > 1 vokser funksjonen raskest for store verdier av x. | |
| − | |||
| − | |||
| − | |||
| − | + | Figuren viser grafene til f(x) = x 0,5 og til g(x) = x 1,5 . | |
| − | + | ===Eksponentialfunksjoner=== | |
| − | + | Dersom vi har en situasjon der noe endrer seg opp eller ned med en fast prosent per tidsenhet, har vi en eksponentiell situasjon og kan lage en eksponentialfunksjon. | |
| + | Funksjoner av typen <br> | ||
| + | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| + | <math> f(x) = a\cdot b^x \\ | ||
| + | (b > 0)</math> | ||
| + | </div><br> | ||
| + | kalles eksponentialfunksjoner | ||
| − | + | Funksjonene illustrerer ofte en eller annen form for vekst. I biologien finnes det populasjoner som, i perioder, vokser tilnærmet etter disse modellene. | |
| + | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| + | '''Eksempel:'''<br> | ||
| + | <math> f(x) = a\cdot b^x \quad \quad | ||
| + | (b > 0)</math> | ||
| + | </div><br> | ||
| − | + | Dersom b > 1 vokser funksjonen med økende x-verdi. Er 1 > b > 0 avtar funksjonen med økende x-verdi. | |
| + | [[Bilde:exp.PNG]] | ||
| − | |||
| + | Figuren viser grafen til f(x) = 0,5x og til g(x) = 1,5x. | ||
| − | + | Man kan bruke et hvilket som helst positivt tall som grunntall (b). Det mest vanlige er [[e]]. | |
| − | |||
| − | |||
| − | + | [http://www.matematikk.net/emner/applets/ggbApplet.php?appid=3 Lek med eksponentialfunksjonen] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Kategori:Analyse]] | |
| − | + | [[Kategori:1P]] | |
| − | + | [[Kategori:2P]] | |
| − | + | [[Kategori:1T]] | |
| + | [[Kategori:R1]] | ||
Nåværende revisjon fra 6. apr. 2024 kl. 03:45
Koordinatsystem
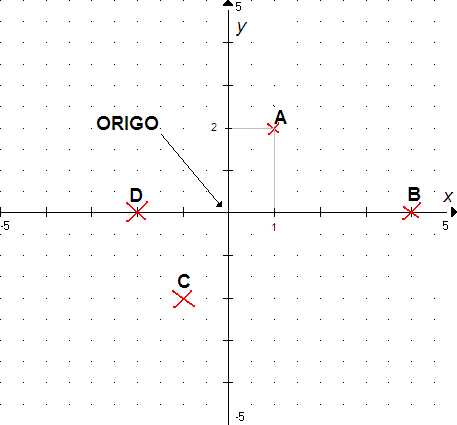
Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for akser. Punktet der aksene krysser hverandre kalles for origo.Begge aksene har verdien null i origo. Den vannrette aksen kalles for x- aksen eller første aksen. Den loddrette aksen kalles for y- aksen eller andre aksen.
Et punkt kan bestemmes med to tall ( et tallpar ) som vi kaller koordinater. Tallpar skrives på formen (x,y). Origo har koordinatene (0, 0). Man oppgir alltid x verdien først . Punktet (1,3) har verdiene x = 1 og y = 3.
Her er eksempler på noen punkter: A (1,2), B (4,0), C (-1, -2), D (-2, 0).
På denne måten kan alle ”steder” (punkter) i et plan representeres, med en x koordinat og en y koordinat. Alle kart er laget på denne måten. X – aksen er da øst - vest retning og Y – aksen er nord – sør retningen.
Lek med koordinatsystemet
Funksjon
Hva er en funksjon?
La oss tenke oss en liten tunnel som det går an å kjøre en bil gjennom. Hver gang en rød bil kjører inn i tunnelen er den blå når den kommer ut. Når en svart bil kjører inn er den blå når den kommer ut. Når en grønn bil kjører inn er den blå når den kommer ut. Når en blå bil kjører inn er den blå når den kommer ut.
Hva er tunnelens funksjon?
Jo, den maler alle biler blå.
La oss tenke oss at vi har en liten boks med et hull i toppen og et i bunnen. Når vi putter et tall inn i toppen kommer et annet tall ut i bunnen. La oss gi boksen vårt et navn. La oss kalle den for Y.
Vi putter tallet 3 inn og får ut tallet 5.
Vi putter tallet 1 inn og får ut tallet 3.
Vi putter tallet 7 inn og får ut tallet 9.
Vi putter tallet -3 inn og får ut tallet -1.
Vi putter tallet -1 inn og får ut tallet 1
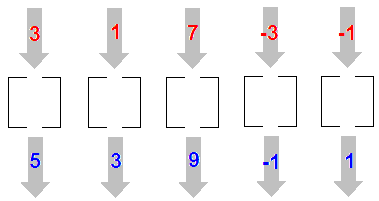
Hva gjør boksen?
Den legger til to til det tallet som blir stappet inn i boksen. Vi kallet boksen for y? La oss kalle tallet vi putter inn for x.
Vi kan skrive dette slik matematisk:
$$y = x + 2$$
$y = x + 2$ kalles for funksjonsutrykket. Vi sier at y er en funksjon av x. Verdien av y avhenger av verdien av x. Detter er det vi kaller en lineær funksjon, dvs. en rett linje.
Funksjonssuttrykk
Funksjonen $f(x) = 2x + 5$ har funksjonsuttrykket $2x + 5$. Uttrykket forteller hva som skal gjøres med tallet som skal inn i funksjonen. I dette tilfellet skal tallet multipliseres med 2 og 5 legges til.
$f$ er navnet på funksjonen. Bokstaven i parantes er navnet på den variable. Vanlige navn er $x$ og $t$. $t$ brukes gjerne om tid. Vanlige funksjonsnavn er $f,g,h$ og $V$, for å nevne noen. Man kan gi en funksjon det navn man ønsker, men det er fornuftig å gi navn som forteller noe om hva funksjonen gjør.
Graf
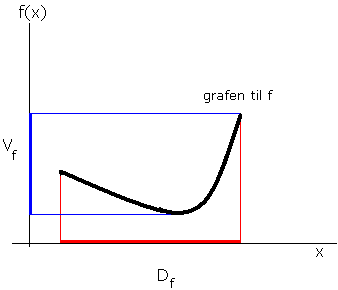
En graf er en kurve (linje) som viser sammenhengen mellom to variable størrelser, for eksempel x og y.
Det er viktig å legge merke til at dersom kurven representerer en funksjon finnes det bare en y-verdi for hver x-verdi. For en y-verdi kan det finnes flere x-verdier. Dersom x er forskjellige tidspunkt på dagen og y er temperaturen, betyr det at et tidspunkt kan kun ha en temperatur, men en temperatur kan ha forekommet flere tider på dagen.
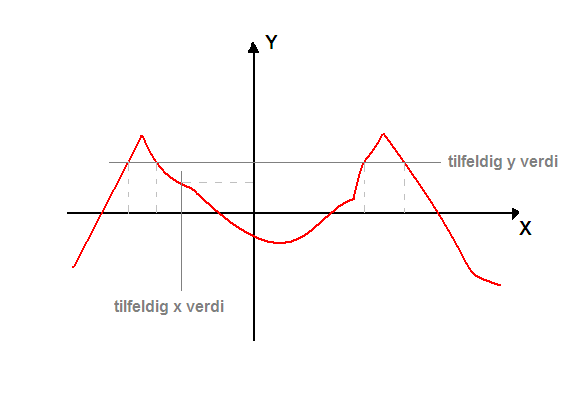
Figuren viser hvordan en tilfeldig x verdi kun kan ha en tilhørende y verdi, mens en tilfeldig y verdi kan ha to eller flere tilhørende x verdier.
Definisjonsmengde
Hvilke verdi den variable kan ha i funksjonen bestemmes av definisjonsmengden D. Dersom funksjonens navn er f, brukes notasjonen <math>D_f = [x_1, x_2]</math>. Alternativt bruker man <math> x \in [x_1, x_2] </math>
Verdimengde
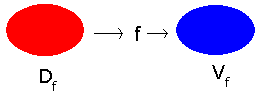
Hvilke verdier som kommer ut av funksjonen, funksjonsverdiene, er bestemt av definisjonsmengden og av funksjonsuttrykket, Mengden av funksjonsverdier verdiene kalles Verdimengden. Om funksjonens navn er f brukes notasjonen <math> V_f </math>.
Man kan se på en funksjon som en ”bro” mellom mengder, definisjonsmengden og verdimengden.
Lek med verdi og definisjonsmengde
Sentrale Punkter på grafen
Nullpunkter
Et nullpunkt er et sted der grafen til en funksjon kysser x -aksen. Dersom vi har funksjonen f(x) finner vi eventuelle nullpunkter ved å løse likningen f(x) = 0. En funksjon kan ha ingen, ett eller flere nullpunkter avhengig av type funksjon, definisjonsområde og koeffisienter. Visuelt finner man nullpunktene ved å lese av verdien på x-aksen, der grafen krysser aksen.
Skjæring med y- akse
f(0) gir skjæring med y- akse. Vi kaller ofte denne verdien konstantleddet. Et interessant punkt når man skal tegne grafen til funksjonen. Vil være startvedien til funksjonen dersom den er definert for x verdier fra og med null og oppover, $x \in[ 0, \rightarrow>$.
Funksjonstyper
Lineære funksjoner
Det at en funksjon er lineær betyr at om vi tegner grafen i et koordinat system med X verdier på førsteaksen og Y verdier på andreaksen får vi en rett linje. Det generelle funksjonsuttrykket er:
$ y = ax + b $ eller $f(x) = ax+b$ som betyr det samme og er en mer vanlig skrivemåte.
a kalles for stigningstallet og b for konstantleddet. Dersom x er null er Y lik b. Konstantleddet b forteller hvor grafen krysser y-aksen. a forteller hvor mange enheter man beveger seg i y rettning (opp eller ned), når man beveger seg en enhet til høyre på x aksen.
Dersom a er positiv betyr det at grafen stiger mot høyre, med økende x verdi. Desto høyere a verdi, desto brattere stiger grafen.
Dersom a er negativ betyr det at Y avtar mot høyre, eller med økende X verdi.
Tallet b forteller hvor grafen krysser Y aksen. Når grafen krysser Y aksen er X verdien lik null.
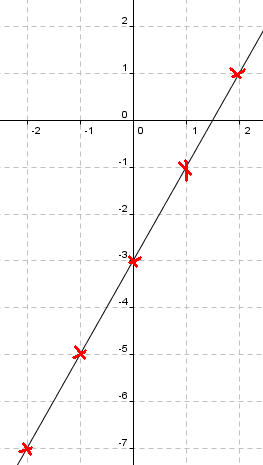
Eksempel 1:
Vi har funksjonsuttrykket:
<math> y = \frac12x + 2 </math>
Grafen ser slik ut:
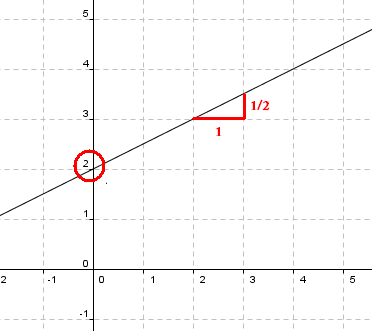
Man observerer at grafen går gjennom punktet (0,2) på y aksen. Stigningstallet er <math>\frac12</math>. Det betyr at når man beveger seg en enhet til høyre må man bevege seg 0,5 (en halv) oppover i y rettning for å treffe grafen igjen.
Dersom man har kontroll på stigningstall og konstantledd er det greit å tegne grafen med bare disse to størrelsene. Dersom man synes dette er vannskelig er det lurt å lage en verditabell.
Verditabell
Vi velger selv tilfeldige X verdier. Det er gjerne lurt å velge verdier som ligger nærheten av origo.
Når vi har valgt en X verdi setter vi den inn for X i funksjonstrykket (1). Da får vi en Y verdi som hører til X verdien.
Disse resultatene setter vi inn i en tabell. Ut i fra disse verdiene tegner vi grafen. I vårt eksempel kan verditabellen se slik ut:
Verditabell er en samling av punkter på grafen, altså sammhørende verdier av x og f(x). Formålet med å lage en verditabell er at du har nok punkter til å kunne tegn eller skissere grafen.
Det anbefales at du lærer deg å bruke kalkulatoren når du skal lage verditabeller.
Av og til er det imidlertid nødvendig å kunne lage tabellen manuelt. Det gjøres ved at du selv velger et antall x verdier i det området du skal tegne grafen. Du setter inn x verdiene i funksjonsuttrykket og finner sammhørende funksjonsverdier. Hvor mange verdier du velger kommer an på hvor nøyaktig du ønsker det. Flere verdier gir økt nøyaktighet.
Eksempel 2:
Vi ønsker å tegne grafen til f(x) = 2x -3 i området fra x = -2 til x = 2.
Vi velger x lik -2, -1, 0, 1, 2 og får:
| x |
f(x)= 2x - 3 | f(x) | (x, f(x)) |
| -2 | f(-2) = 2 (-2) - 3 | f(-2)= -7 | (-2, -7) |
| -1 | f(-1) = 2 (-1) – 3 | f(-1) = -5 | (-1,-5) |
| 0 | f(0) = 2 (0) – 3 | f(0)= -3 | (0, -3) |
| 1 | f(1) = 2 (1)– 3 | f(1)= - 1 | (1, -1) |
| 2 | f(2) = 2 (2) – 3 | f(2) = 1 | (2, 1) |
Og grafen ser slik ut:
Ettpunktsformelen
Dersom du kjenner et punkt på linjen og stigningstallet kan du finne funksjonsutrykket ved å bruke følgende formel:
<math> y-y_1 = a(x-x_1) </math>
a er stigningstallet og <math>(x_1 , y_1) </math> er koordinatene til punktet.
Eksempel 3:
Hva er funksjonsuttrykket til en funksjon som har stigningstall 2 og går gjennom punktet (-2,-1)?
<math> y-(-1) = 2(x-(-2)) </math>
<math> y = 2x + 3 </math>
Topunktsformelen
Dersom man kjenner to punkter på en rett linje er stigningstallet a gitt som:
<math> a =\frac{\Delta y}{\Delta x}=\frac{y_2 - y_1}{x_2 - x_1} </math>
Desom man setter dette uttrykket inn i etpunktsformelen over får man:<math> y- y_1=\frac{y_2 - y_1}{x_2 - x_1}(x-x_1) </math>
Eksempel 4:
En lineær funksjon gpr gjennom punktene (1,4) og (3,5). Finn funksjonsuttrykket.
Andregradsfunksjoner
Funksjonsuttrykket til en andregradsfunksjon er gitt som
<math> f(x) = ax^2 + bx + c </math>
Gitt på denne formen er <math>ax^2</math> andregradsleddet, bx er førstegradsleddet og c er konstantleddet. Grafene til andregradsfunksjoner kalles parabler. Grafene krummer og er symmetriske om symmetriaksen som er gitt som:
Symmetriakse:
<math> x = \frac{-b}{2a}</math>
Eksempel 5:
Finn symmetriaksen til funksjonen
<math> f(x) = -x^2 + 2x + 4 </math>
Løsning:
<math> x = \frac{-b}{2a} =\frac{-2}{2 \cdot (-1)} =1</math>
Dersom konstanten a i andregradsleddet er positiv vender grafen sin hule side oppover, den ”smiler”
Dersom konstanten er negativ vender grafen sin hule side nedover, den er ”sur”.
En andregradsfunksjon kan også være gitt på formen
<math> f(x) = a(x + b)^2 + c </math>
Konstanten a vil være den samme i begge fremstillingsmåter, men konstantene b og c er forskjellige. Hvilke fremstillingsmåte man benytter er smak og behag, men begge har sine fordeler.
Eksempel 6:
<math>f(x) = a(x + b)^2 + c </math>
Grafen nedenfor viser funksjonen
I f(x) = 0,4x2 -2x +1
eventuelt
II f(x) = 0,4(x -2,5)2 -1,5
Fordelen med utrykk I er at det er på formen man bruker i ”abc” formelen, for å finne nullpunkter.
Fordelen med uttrykk II er at det gir symmetriakse og minimumspunkt direkte. Dersom man multipliserer ut parentesene og trekker sammen ender man opp med uttrykk I.
Rasjonale funksjoner
Funksjoner der x inngår som en del av nevneren kalles brøkfunksjoner eller asymptotiske funksjoner. . Funksjonene går ofte mot en grense når x går mot en bestemt verdi. Dette kalles for asymptoter.
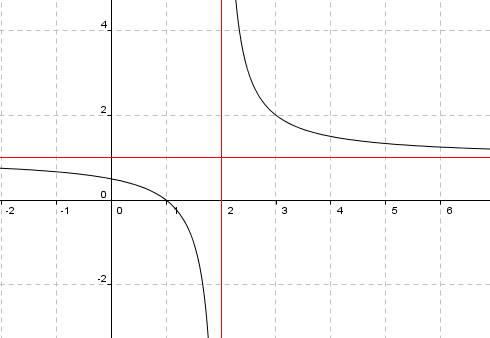
En rett linje som grafen til f(x) nærmer seg når x går mot en bestemt verdi eller <math> \pm \infty </math>. En graf kan godt krysse en asymptote. Vi har vertikale og horisontale (eller skrå) asymptoter.
Figuren viser grafen til funksjonen <math>f(x)= \frac{x-1}{x-2}</math>
Vi ser at grafen har en vertikal asymptote for x = 2 og en horisontal asymptote for y = 1.
Vertikal asymptote
Dersom f (x) går mot pluss / minus uendelig når x nærmer seg et tall a fra den ene eller andre siden (eller begge) så er linjen X = a en vertikal asymptote for f. Dette kan formuleres slik:
<math> \lim\limits_{x \to a^+} f(x)= \pm \infty \quad \quad \quad \lim\limits_{x \to a^-} f(x)= \pm \infty </math>
I eksempelet over er a = 2.
Horisontal (og skrå) asymptote
For å finne den horisontale asymptoten må vi undersøke hva som skjer med verdien av f (x) når x går mot ± uendelig. Dette skrives slik:
<math> \lim\limits_{x \to \infty} f(x)= k \quad \quad \quad \lim\limits_{x \to - \infty} f(x)= k </math>
Dette leses "grenseverdien til f (x) når x går mot pluss / minus uendelig". Dersom et eller begge kriteriene er oppfylt er linjen y = k en horisontal asymptote for f.
For å kunne se hva f går mot når x går mot ± uendelig kan det være nødvendig å foreta en polynomdivisjon. Dersom <math>f(x)= \frac{h(x)}{g(x)} </math> utfører vi divisjonen. Dersom vi gjør det med eksempelet over ser vi at f (x) kan skrives som <math>f (x) = 1+ \frac{1}{x-2}</math>. Nå ser vi lett at f går mot 1 når x går mot ± uendelig.
Når teller og nevner er av samme orden blir asymptoten en horisontal linje. Dersom telleren h (x) er en orden over nevneren får vi en skrå asymptote. Dersom vi har funksjonen <math>f (x)= \frac{3x^2 + 2x -5}{x} </math>og utfører divisjonen ser vi at den kan skrives som <math>f (x)= 3x + 2 - \frac 5x</math>. Vi ser at når x går mot ± uendelig går f mot den rette linjen 3x + 2. Grafen ser slik ut:
Polynomfunksjoner
Funksjoner som består av flere ledd. Både rettlinjede funksjoner og andregradsfunksjoner er polynomfunksjoner, men så sentrale at de behandles spesielt.
Generelt er polynomfunksjoner gitt ved:
<math> f(x) = a\cdot x^n + b\cdot x^{n-1}+ ...+ c </math>
Der n er hele positive tall.
På vgs. befatter vi oss av og til med funksjoner av 3. og 4. grad, men sjelden funksjoner av høyere grad.
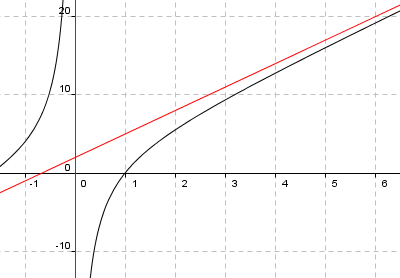
Potensfunksjoner
Potensfunksjoenr er av typen:
<math>f(x) = a\cdot x^b </math>
der x og b >0
Eksempel:
$ f(x) = a\cdot b^x$
(Dersom b = -1 har vi en asymptotisk funksjon hvis graf er en hyperbel. Dersom b = 1 får man en rett linje gjennom origo, med stigning en. Legg merke til at f(1) = a, fordi 1b er 1 uansett b - verdi.)
Dersom 1>b>0 vokser funksjonen raskest for små verdier av x, for så å avta noe (avhengig av b). Dersom b > 1 vokser funksjonen raskest for store verdier av x.
Figuren viser grafene til f(x) = x 0,5 og til g(x) = x 1,5 .
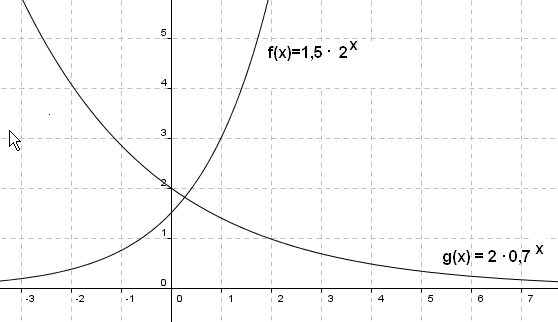
Eksponentialfunksjoner
Dersom vi har en situasjon der noe endrer seg opp eller ned med en fast prosent per tidsenhet, har vi en eksponentiell situasjon og kan lage en eksponentialfunksjon.
Funksjoner av typen
<math> f(x) = a\cdot b^x \\ (b > 0)</math>
kalles eksponentialfunksjoner
Funksjonene illustrerer ofte en eller annen form for vekst. I biologien finnes det populasjoner som, i perioder, vokser tilnærmet etter disse modellene.
Eksempel:
<math> f(x) = a\cdot b^x \quad \quad
(b > 0)</math>
Dersom b > 1 vokser funksjonen med økende x-verdi. Er 1 > b > 0 avtar funksjonen med økende x-verdi.
Figuren viser grafen til f(x) = 0,5x og til g(x) = 1,5x.
Man kan bruke et hvilket som helst positivt tall som grunntall (b). Det mest vanlige er e.