Forskjell mellom versjoner av «Eksponentialfunksjonen»
Fra Matematikk.net
(Ny side: Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler ...) |
m (Teksterstatting – «</tex>» til «</math>») |
||
| (9 mellomliggende revisjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
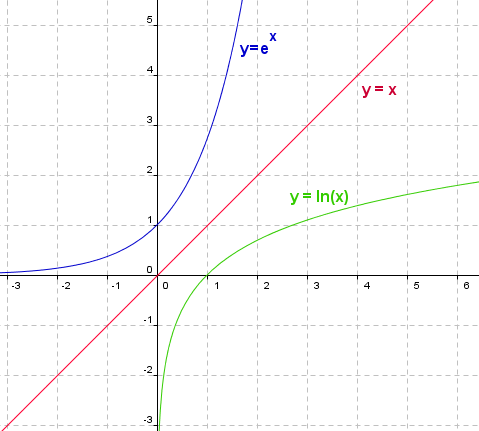
| − | Den naturlige eksponentialfunksjonen | + | Den naturlige eksponentialfunksjonen <math>e^x</math> er definert som <math>e^x = y</math> dersom, og bare dersom ln(y) = x for alle x der y > 0. <math>e^x</math> skrives også exp (x). ln(x) og <math>e^x</math> er inverse funksjoner og speiler hverandre om linjen y = x. |
| − | + | [[Bilde:Exp1lex.png]] | |
Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende: | Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende: | ||
| − | + | <math> e^p \cdot e^q = e^{(p+q)} </math> | |
| − | + | <math> \frac{e^p}{e^q} = e^{(p-q)} </math> | |
| − | + | <math> (e^p)^q = e^{(p\cdot q)} </math> | |
| − | + | <p></p> | |
| + | |||
| + | [[http://www.matematikk.net/emner/applets/ggbApplet.php?appid=3 "Utforsk eksponentialfunksjonen her"]] | ||
---- | ---- | ||
[[Kategori:lex]] | [[Kategori:lex]] | ||
Nåværende revisjon fra 5. feb. 2013 kl. 20:58
Den naturlige eksponentialfunksjonen <math>e^x</math> er definert som <math>e^x = y</math> dersom, og bare dersom ln(y) = x for alle x der y > 0. <math>e^x</math> skrives også exp (x). ln(x) og <math>e^x</math> er inverse funksjoner og speiler hverandre om linjen y = x.
Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende:
<math> e^p \cdot e^q = e^{(p+q)} </math>
<math> \frac{e^p}{e^q} = e^{(p-q)} </math>
<math> (e^p)^q = e^{(p\cdot q)} </math>
["Utforsk eksponentialfunksjonen her"]