Forskjell mellom versjoner av «Eksponentialfunksjonen»
Fra Matematikk.net
(Ny side: Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler ...) |
|||
| Linje 1: | Linje 1: | ||
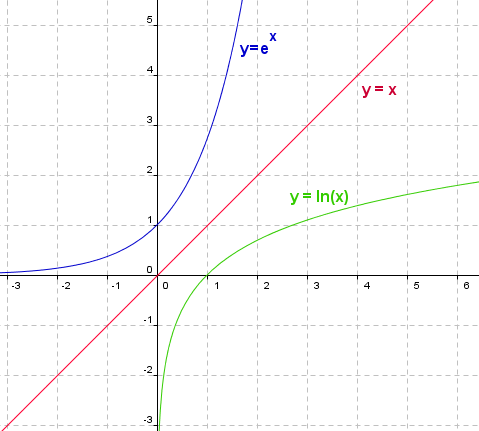
Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler hverandre om linjen y = x. | Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler hverandre om linjen y = x. | ||
| − | + | [[Bilde:Exp1lex.png]] | |
Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende: | Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende: | ||
Revisjonen fra 3. jul. 2011 kl. 12:35
Den naturlige eksponentialfunksjonen ex er definert som ex = y dersom, og bare dersom ln(y) = x for alle x der y > 0. ex skrives også exp (x). ln(x) og ex er inverse funksjoner og speiler hverandre om linjen y = x.
Dersom p og q er reelle tall og r er et rasjonalt tall har vi følgende:
• epeq = ep+q
• ep / eq = ep-q
• (ep)r = epr
Nedenfor er det plottet noen forskjellige funksjonen der eksponentialfunksjonen inngår.