Forskjell mellom versjoner av «2P 2020 høst LØSNING»
| (9 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 239: | Linje 239: | ||
===b)=== | ===b)=== | ||
| − | [[File: | + | [[File: 2P_H20_del2_4b1.png]] |
| − | [[File: | + | [[File: 2P_H20_del2_4b2.png]] |
Elin vil ha 149 918,63 kroner på kontoen rett etter at hun har satt inn 10 000 kr første januar 2025. | Elin vil ha 149 918,63 kroner på kontoen rett etter at hun har satt inn 10 000 kr første januar 2025. | ||
| + | |||
| + | ==Oppgave 5== | ||
| + | |||
| + | ===a)=== | ||
| + | |||
| + | Bruker Excel. | ||
| + | |||
| + | [[File: 2P_H20_del2_5a1.png]] | ||
| + | |||
| + | [[File: 2P_H20_del2_5a2.png]] | ||
| + | |||
| + | Gjennomsnittlig snødybde på julaften i Oslo de 11 siste årene er 5,45 cm. Standardavviket er 5,73 cm. | ||
| + | |||
| + | Gjennomsnittlig snødybde på julaften i Kautokeino de 11 siste årene er 41 cm. Standardavviket er 9,24 cm. | ||
| + | |||
| + | ===b)=== | ||
| + | |||
| + | Påstanden er ikke riktig. Standardavviket sier noe om spredningen i tallmaterialet. Vi kan ha et datamateriale med høyt gjennomsnitt, men med mange tilnærmet like verdier; da vil standardavviket være lite selv om gjennomsnittet er høyt. Omvendt kan det være et datamateriale med mange veldig forskjellige verdier, som gir et høyt standardavvik uavhengig av gjennomsnittet. | ||
| + | |||
| + | ==Oppgave 6== | ||
| + | |||
| + | ===a)=== | ||
| + | |||
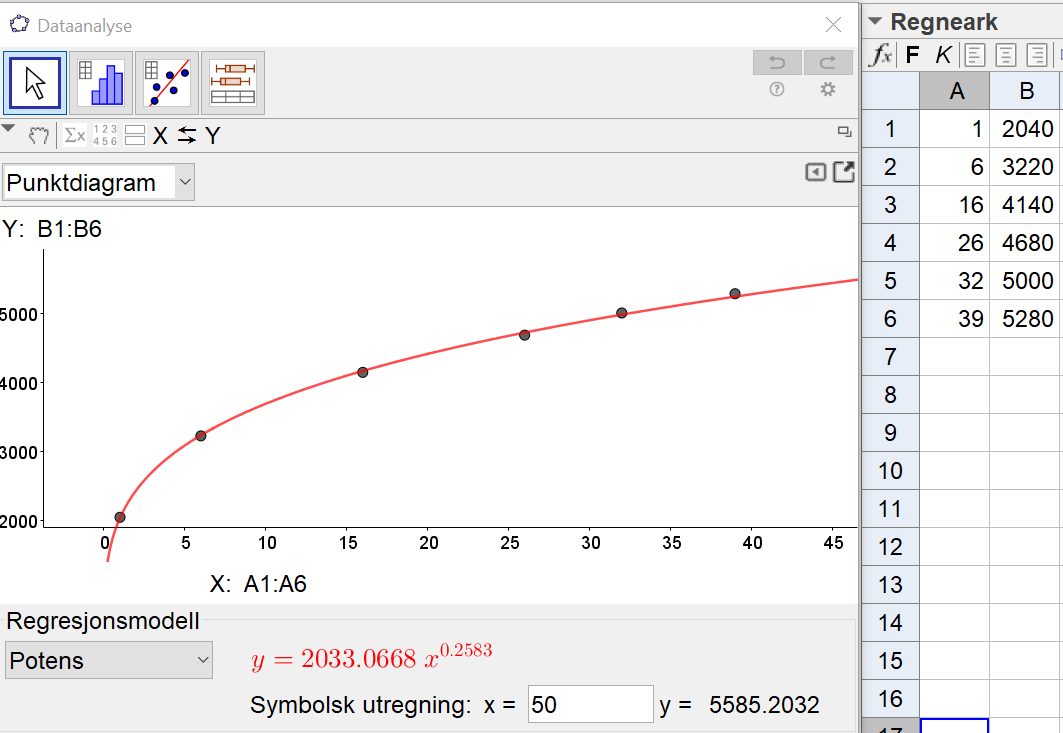
| + | Bruker Geogebra, legger inn dataene i regnearket, og bruker "regresjonsanalyse". | ||
| + | |||
| + | [[File: 2P_H20_del2_6b.png]] | ||
| + | |||
| + | Jeg velger en potensfunksjon som modell. Denne passer godt med punktene og flater ut etter hvert slik Svein antar. Modellen for antall innbyggere x år etter 1980 er $f(x) = 2033\cdot x^{0,2583}$ | ||
| + | |||
| + | ===b)=== | ||
| + | |||
| + | Det vil være 5585 innbyggere i boliområdet i 2030 (x=50) ifølge modellen (se "symbolsk utregning" nederst på skjermbildet i oppgave a). Dette stemmer godt med Sveins antakelse om at antall innbyggere vil øke, men at økningen vil avta. | ||
| + | |||
| + | ==Oppgave 7== | ||
| + | |||
| + | ===a)=== | ||
| + | |||
| + | Avtale 1: $y=1200\,kr\cdot 28 + 22000\,kr = 55600\,kr$ | ||
| + | |||
| + | Avtale 2: $y=600\,kr \cdot 28 + 28000 \, kr= 44800\,kr$ | ||
| + | |||
| + | Avtale 3: $y=200\,kr\cdot 28 + 50000\,kr = 55600\,kr$ | ||
| + | |||
| + | ===b)=== | ||
| + | |||
| + | Bruker CAS i Geogebra: | ||
| + | |||
| + | [[File: 2P_H20_del2_7b.png]] | ||
| + | |||
| + | Med avtale 1 kan kunden leie leiligheten i 25 døgn før den totale prisen overstiger 53 000 kroner. For avtale 2 er det 41 døgn, og for avtale 3 er det 15 døgn. | ||
| + | |||
| + | ===c)=== | ||
| + | |||
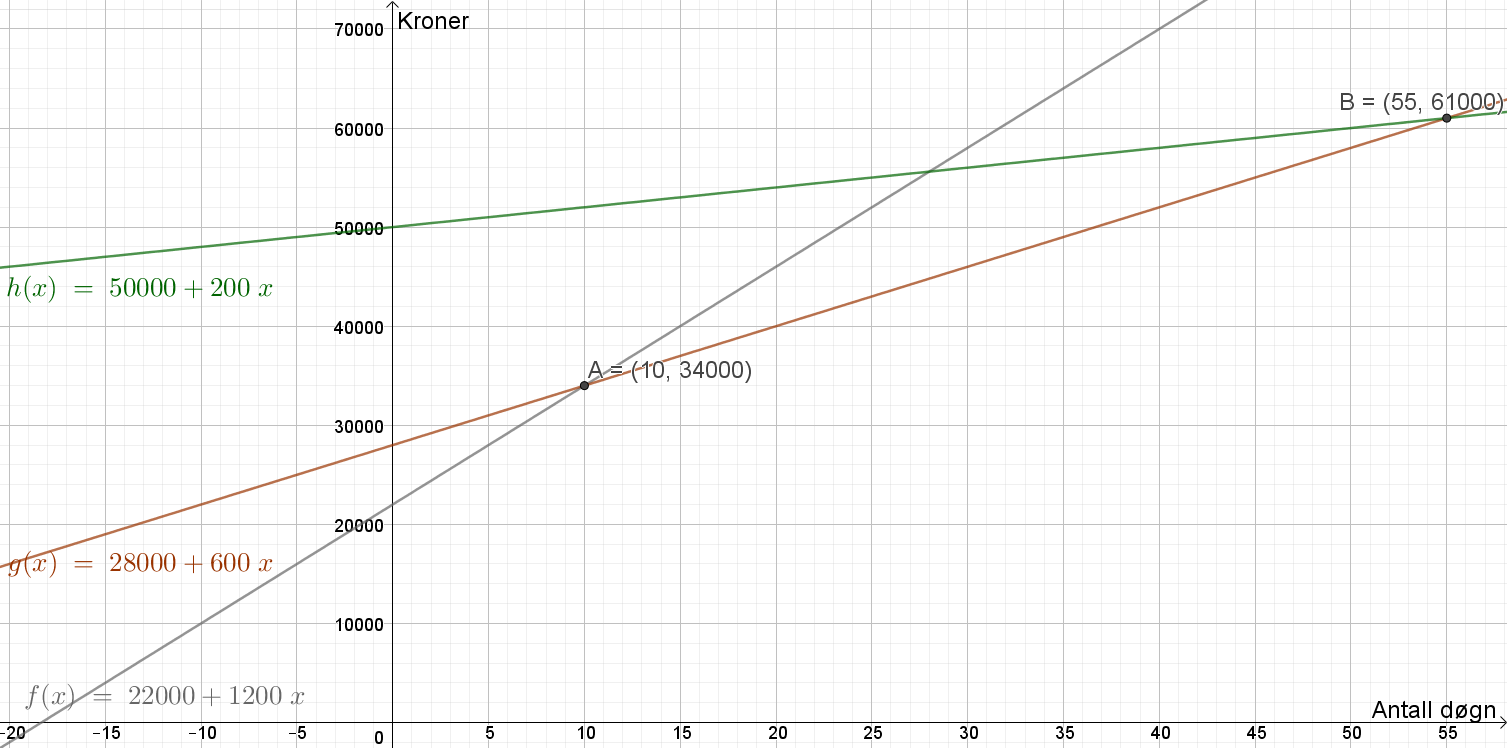
| + | Bruker Geogebra og tegner grafen til funksjonene. | ||
| + | |||
| + | [[File: 2P_H20_del2_7c.png]] | ||
| + | |||
| + | Avtale 1 lønner seg frem til 10 døgn leie, Avtale 2 lønner seg fra 10 til 55 døgn leie, og avtale 3 lønner seg fra 55 døgn leie. | ||
| + | |||
| + | ==Oppgave 8== | ||
| + | |||
| + | ===a)=== | ||
| + | |||
| + | Ser på diagrammet for maksimumstemperaturen i Oslo hvert døgn i januar 2020. | ||
| + | |||
| + | Medianen er ca. $5,6^{\circ}C$. Det er representert ved den vannrette streket i den grønne boksen. Jeg vet dette fra å ha sammenlignet med diagrammet for Trondheim, hvor jeg vet at medianen er $6^{\circ}C$. | ||
| + | |||
| + | Gjennomsnittet er ca. $5^{\circ}C$. Det er representert ved krysset i den grønne boksen. | ||
| + | |||
| + | Variasjonsbredden er ca. $9^{\circ}C-1,5^{\circ}C=7,5^{\circ}C$. Det er avstanden mellom største og minste verdi på diagrammet. | ||
| + | |||
| + | Kvartilbredden er ca. $6,9^{\circ}C-3,7^{\circ}C=3,2^{\circ}C$. Det er avstanden mellom største og minste verdi på den grønne boksen (altså 3. og 1. kvartil). | ||
| + | |||
| + | ===b)=== | ||
| + | |||
| + | Vi ser at 1. kvartil på begge diagrammene er på ca. $3,6^{\circ}C$. Det vil si at en fjerdedel av dagene i januar hadde en maksimumstemperatur på $3,6^{\circ}C$ eller lavere. En fjerdedel av 31 dager er nesten 8 dager. | ||
Nåværende revisjon fra 4. des. 2020 kl. 20:06
Diskusjon av oppgaven på matteprat
Mer diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
Rangerer tallene i stigende rekkefølge:
$7\quad10\quad10\quad12\quad12\quad18\quad20\quad20\quad33\quad38$
Medianen er gjennomsnittet av de to midterste tallene: $\frac{12+18}{2}=\frac{30}{2}=15$
Gjennomsnitt: $\frac{7+10+10+12+12+18+20+20+33+38}{10}=\frac{180}{10}=18$
Medianen er 15 og gjennomsnittet er 18 for antall bilder som passerte i løpet av en periode med grønt lys.
b)
Hvis vi ser på den sorterte listen i a), ser vi at 18 er det sjette tallet. Det betyr at den kumulative frekvensen for 18 passerte biler er 6. Det forteller oss at det passerte 18 eller færre biler i løpet av en periode med grønt lys i 6 av observasjonene.
c)
Dersom tiden med grønt lys var kortet ned med 10 %, antar jeg at medianen og gjennomsnittet også ville synke med 10 %.
Ny median: $15-\frac{10\cdot 15}{100} = 15-1,5 = 13,5$ passerte biler i løpet av en periode med grønt lys.
Nytt gjennomsnitt: $18-\frac{10\cdot 18}{100}=18-1,8=16,2$ passerte biler i løpet av en periode med grønt lys.
Oppgave 2
$\frac{5\cdot 10^{12}+3,1\cdot 10^{13}}{1,8\cdot 10^7} = \frac{0,5\cdot 10^{13}+3,1\cdot 10^{13}}{1,8\cdot 10^7} = \frac{(0,5+ 3,1)\cdot 10^{13}}{1,8\cdot 10^7} = \frac{3,6\cdot 10^{13}}{1,8\cdot 10^7} = 2\cdot 10^{13-7} = 2\cdot 10^6 $
Oppgave 3
a)
| Høyde i cm | Klassemidtpunkt, $x_m$ | Frekvens, $f$ | $f\cdot x_m$ |
| $[150,160\rangle$ | $155$ | $10$ | $1550$ |
| $[160,170\rangle$ | $165$ | $30$ | $4950$ |
| $[170,180\rangle$ | $175$ | $50$ | $8750$ |
| $[180,200\rangle$ | $190$ | $10$ | $1900$ |
| Sum | $100$ | $17150$ |
Gjennomsnitt: $\frac{17150}{100}=171,5\,cm$
Gjennomsnittshøyden til elevene ved skolen er 171,5 cm.
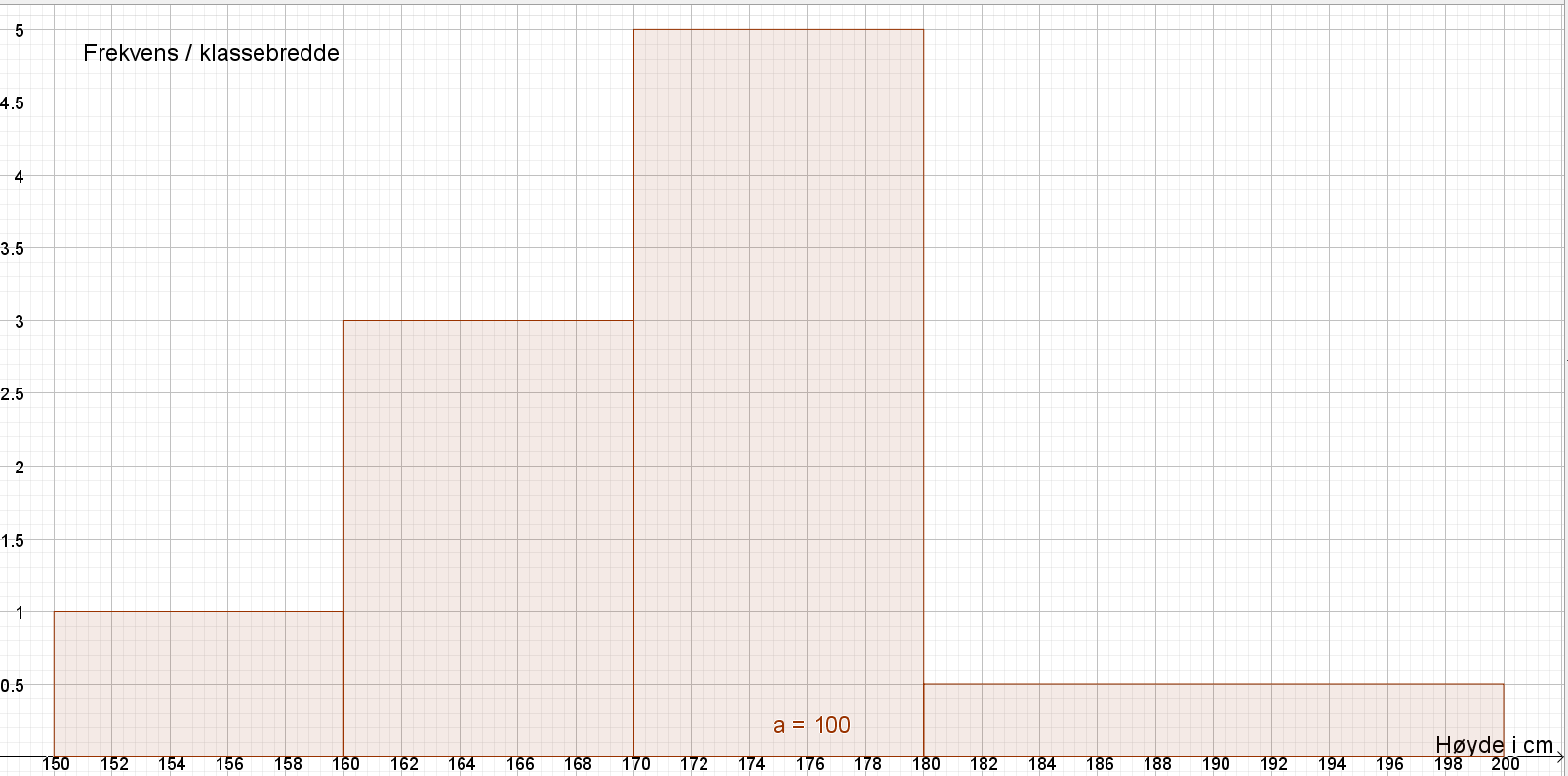
b)
| Høyde i cm | Klassebredde, $b$ | Frekvens, $f$ | Histogramhøyde, $\frac{f}{b}$ |
| $[150,160\rangle$ | $160-150=10$ | $10$ | $\frac{10}{10}=1$ |
| $[160,170\rangle$ | $170-160=10$ | $30$ | $\frac{30}{10}=3$ |
| $[170,180\rangle$ | $180-170=10$ | $50$ | $\frac{50}{10}=5$ |
| $[180,200\rangle$ | $200-180=20$ | $10$ | $\frac{10}{20}=0,5$ |
PS: du må tegne histogrammet for hånd, siden dette er del 1.
Oppgave 4
NB: siden dette er del 1, må du lage en skisse av disse grafene for hånd. Du må angi hvilke størrelser som er på x- og y-aksen, og skrive noen tall som passer på x- og y-aksen, spesielt i skjæringspunktene mellom grafen og aksene.
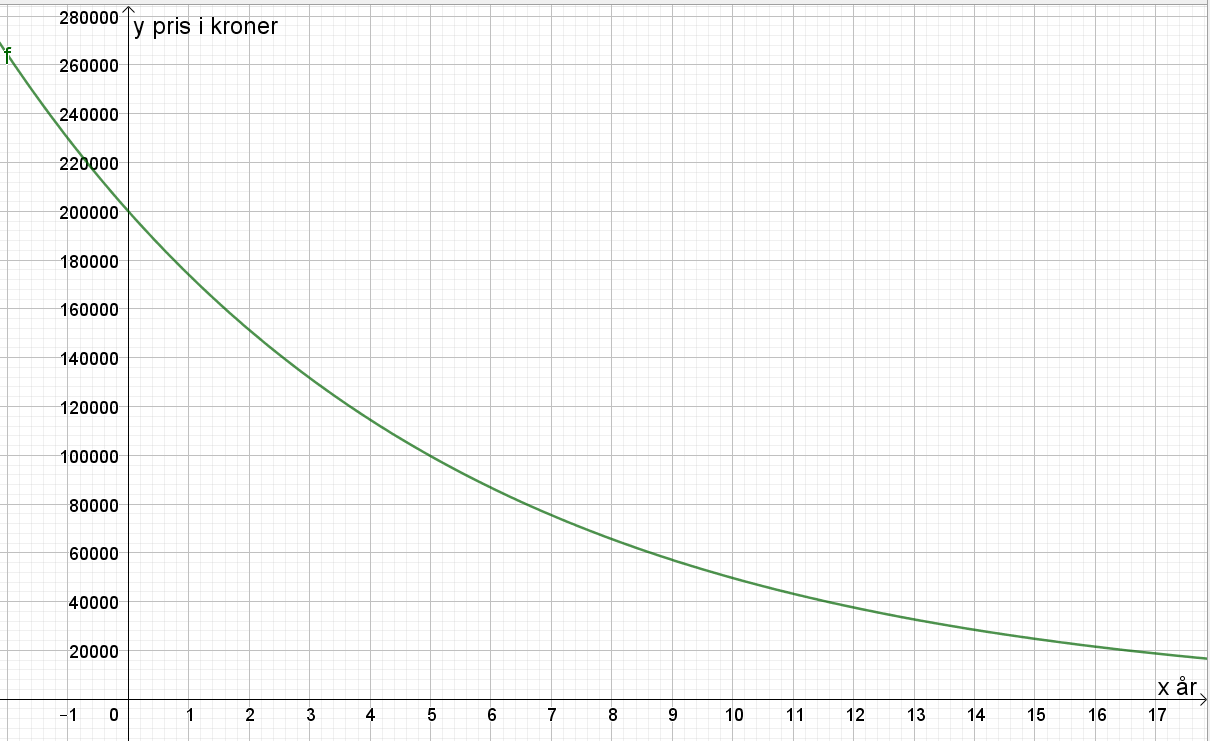
Situasjon 1: en eksponentiell modell beskriver bilens verdi som funksjon av x antall år.
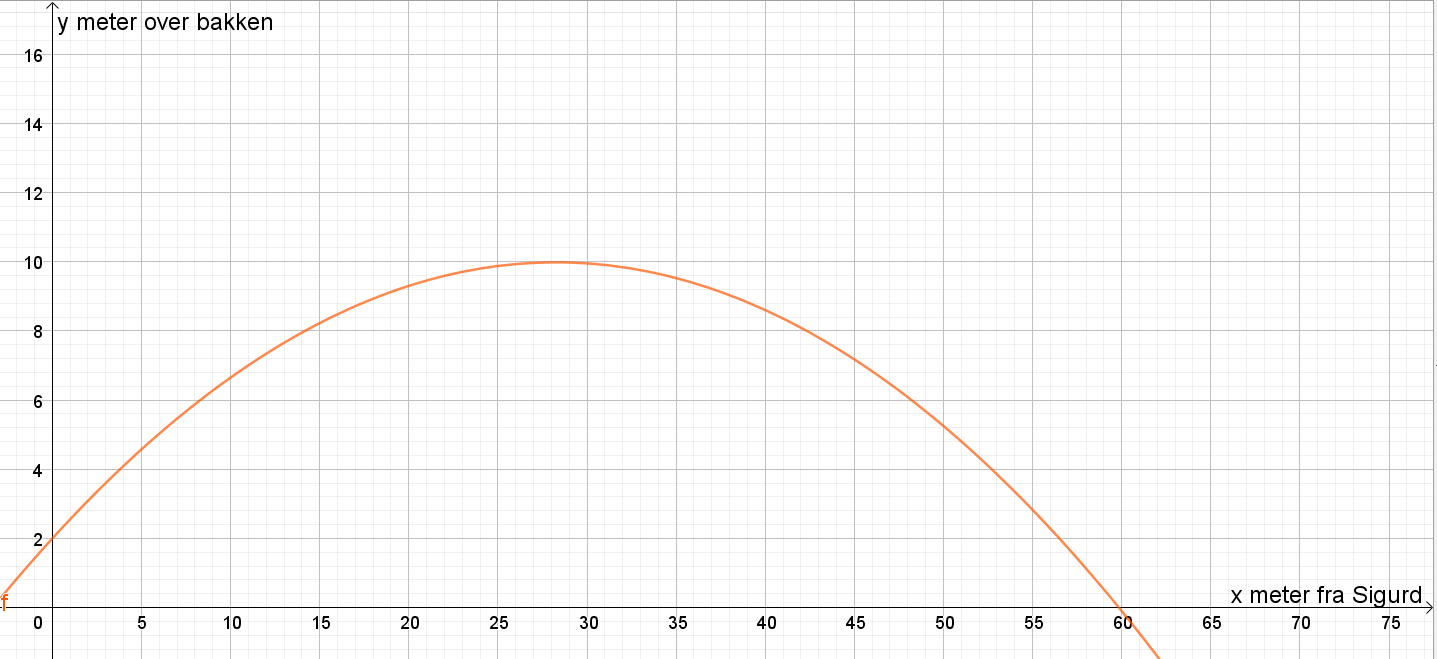
Situasjon 2: en andregradsfunksjon beskriver spydets høyde som en funksjon av avstanden fra Sigurd.
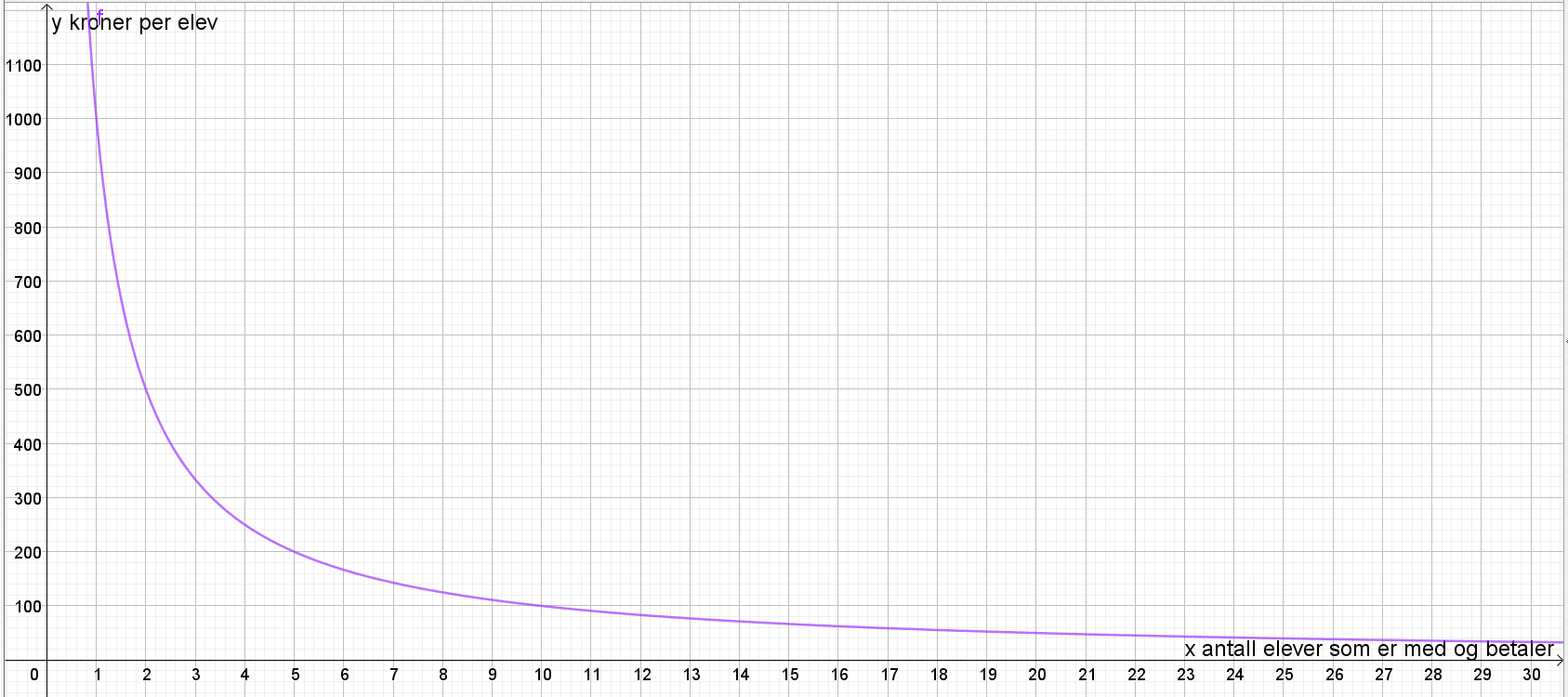
Situasjon 3: en omvendt proporsjonal funksjon beskriver hvor mye hver elev må betale som funksjon av antall elever som blir med på gaven.
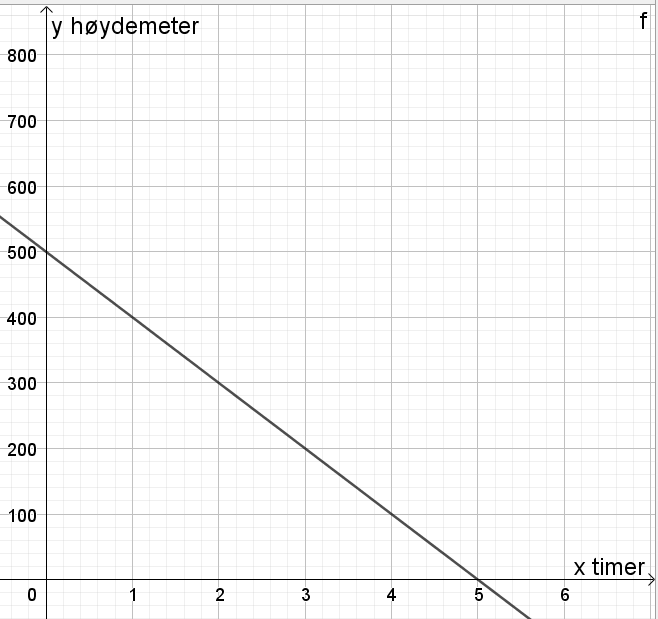
Situasjon 4: en lineær funksjon beskriver hvor mange høydemeter Ulrikke befinner seg på som funksjon av tiden.
Oppgave 5
Velger punktet (1989, 18 000) som startpunkt, og punktet (2019, 30 000) som sluttpunkt.
Finner stigningstallet til en rett linje som går gjennom de to punktene:
$a=\frac{y_2-y_2}{x_2-x_1}=\frac{30000-18000}{2019-1989}=\frac{12000}{30}=400$
En lineær modell som tilnærmet beskriver utviklingen i denne perioden er $y=400x+18000$, der x er antall år etter 1989.
Oppgave 6
a)
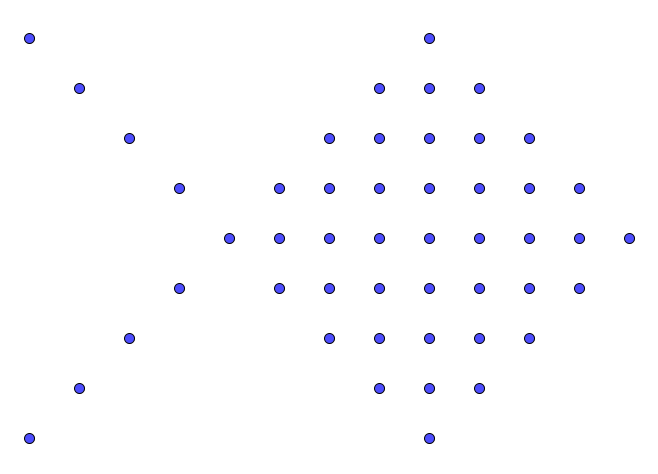
Tegner figur 4, og teller antall sirkler. Det vil være 49 sirkler i figur 4.
b)
Legger sammen lyse sirkler i "halen"+ lyse sirkler i "kroppen" + mørke sirkler for alle figurene, og prøver å finne et mønster.
Figur 1: $2+1+4 = 2\cdot1+1\cdot1+2\cdot2 = 7$
Figur 2: $4+4+9 = 2\cdot2+2\cdot2+3\cdot3 = 17$
Figur 3: $6+9+16 = 2\cdot3+3\cdot3+4\cdot4=31$
Figur 4: $8+16+25= 2\cdot4+4\cdot4+5\cdot5=49$
Figur n: $\quad 2\cdot n+n\cdot n+(n+1)\cdot(n+1) \\ =2n+n^2+ (n^2+2n+1) \\ = 2n^2+4n+1$
Antall sirkler i figur n kan uttrykkes ved $F_n=2n^2+4n+1$.
c)
$F_n=2n^2+4n+1 \\ F_{20} = 2\cdot 20^2 + 4\cdot 20 + 1 = 2\cdot 400+80+1=881$
Det vil være 881 sirkler i figur 20.
DEL 2
Oppgave 1
a)
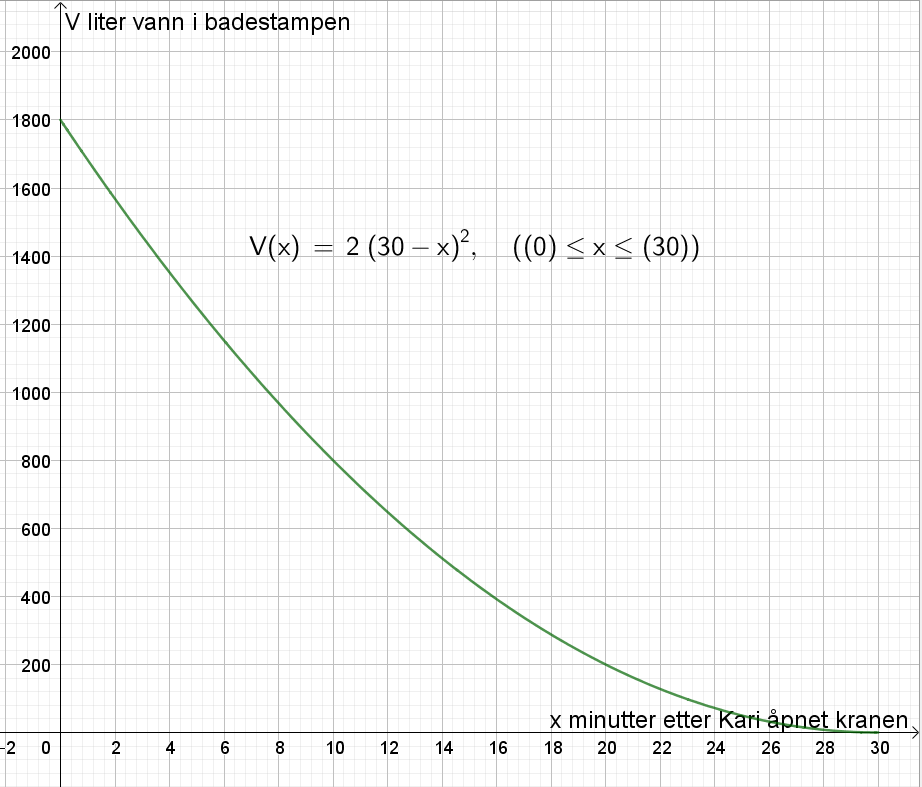
Tegner grafen til V i Geogebra.
b)
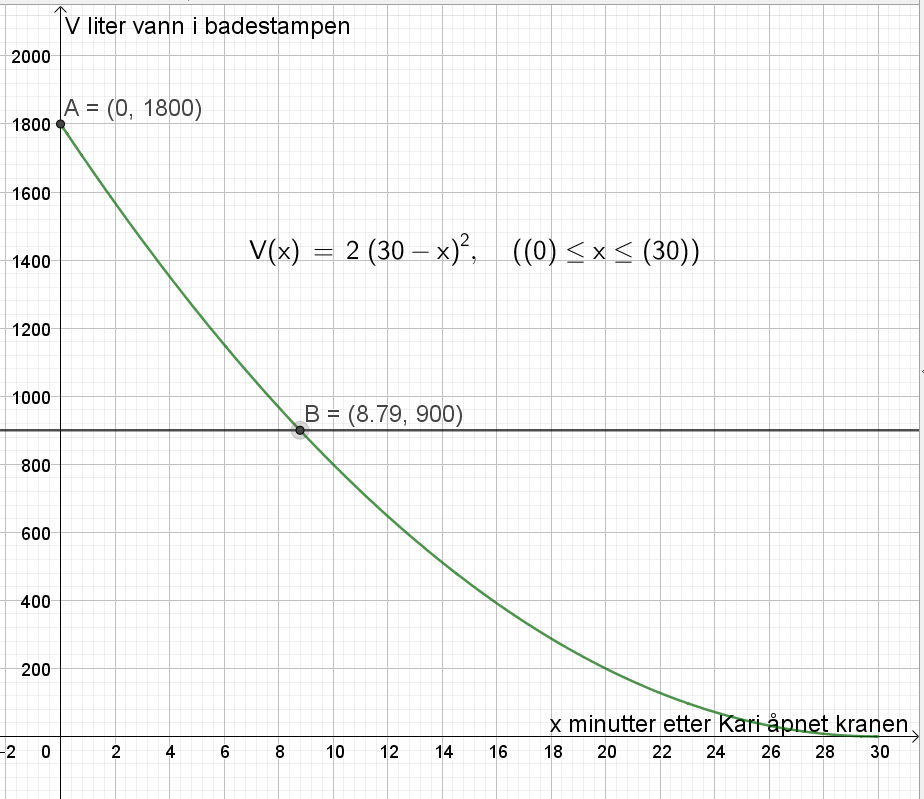
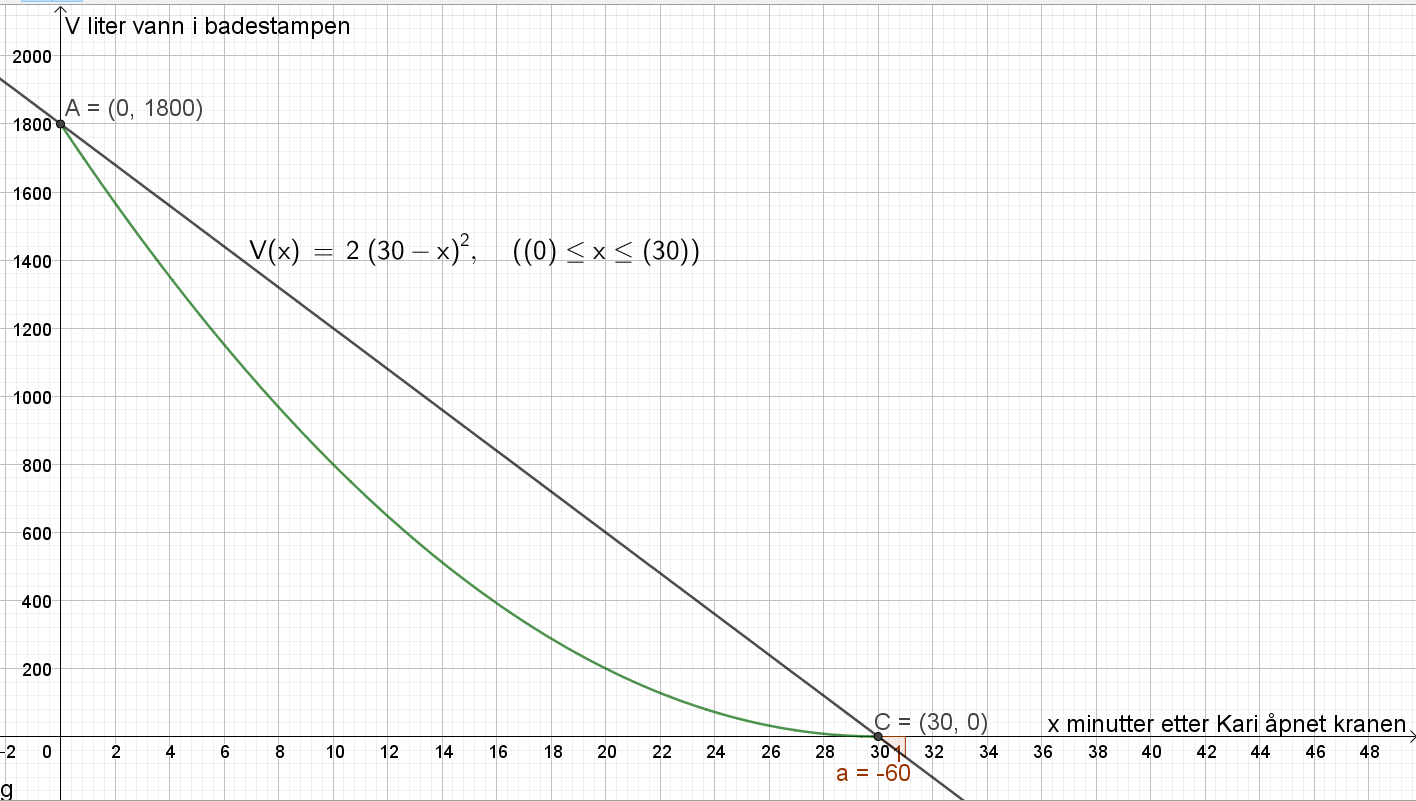
Finner skjæringspunktet med y-aksen, A=(0,1800). Det betyr at det var 1800 L vann i badestampen til å begynne med. 900 L tilsvarer da halvparten av vannet.
Lager linjen y = 900, og finner skjæringspunktet mellom denne linjen med grafen til V, B=(8.79, 900).
Det tar 8,79 minutter, det vil si omtrent 8 minutter og 47 sekunder, å tappe ut halvparten av vannet. ($0,79min\cdot 60sek/min=47 sek$).
c)
Finner skjæringspunktet med x-aksen, C=(30,0). Lager en linje som går gjennom punkt A og C med knappen "linje", og finner stigningen til linjen med knappen "stigning". Stigningstallet a = -60.
Det renner ut i gjennomsnitt 60 L vann per minutt fra Kari åpner kranen, til badestampen er tom.
d)
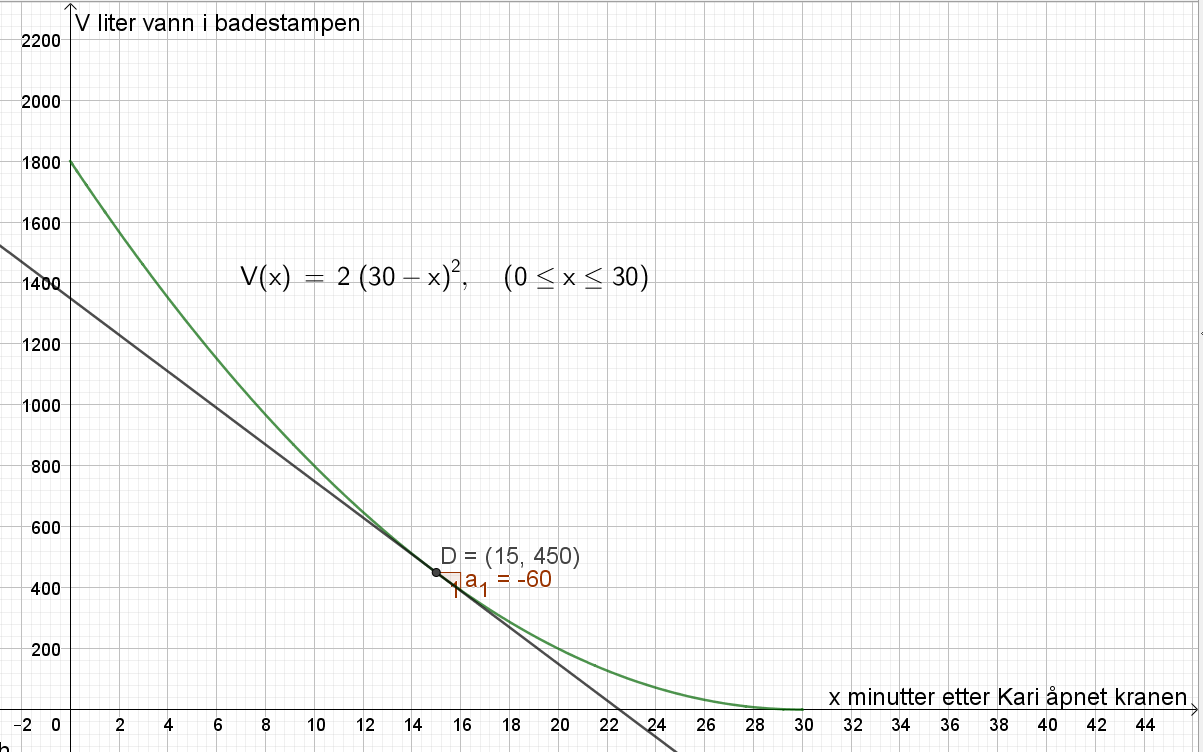
Lager punktet D=(15,V(15)). Lager tangenten med kommandoen "Tangent(punkt, funksjon)". Finner stigningstallet til tangenten med knappen "stigning". Stigningstallet a1 = -60.
Den momentane vekstfarten til funksjonen V når x = 15 er -60 liter vann per minutt. Det betyr at 15 minutter etter at Kari har åpnet kranen, renner det ut 60 L vann per minutt.
Oppgave 2
$15\,min = \frac{15\,min}{(60\,min/t) \cdot (24\,t/døgn) \cdot (365\,døgn/år)}= \frac{1}{35040} \approx 0,0000285 \, år = 2,85 \cdot 10^{-5} \, år$
15 minutter tilsvarer $ 2,85 \cdot 10^{-5}$ år.
Oppgave 3
Vekstfaktor: $1-0,201=0,799$
Antall importerte juletrær i 2009: $\frac{208225}{0,799}=260607$
Det ble importert 260607 juletrær til Norge i 2009.
Oppgave 4
a)
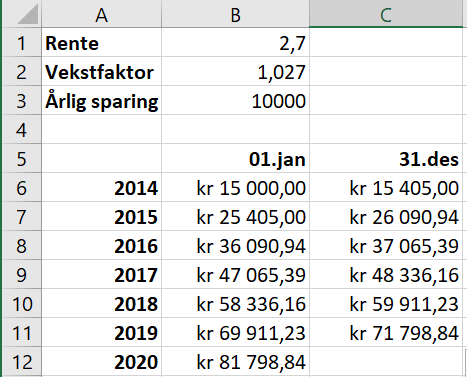
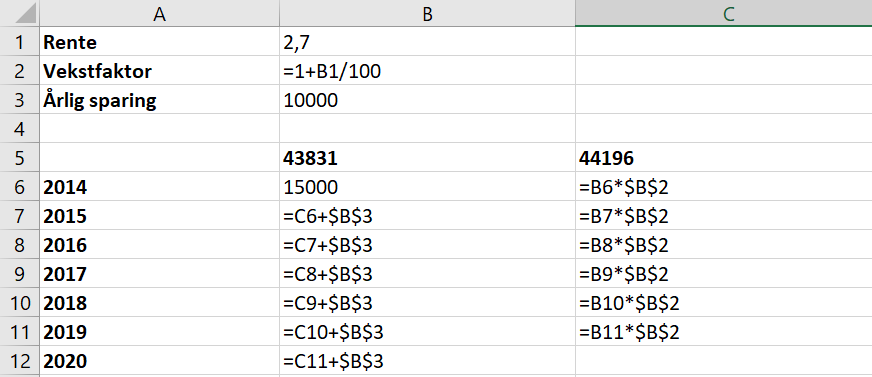
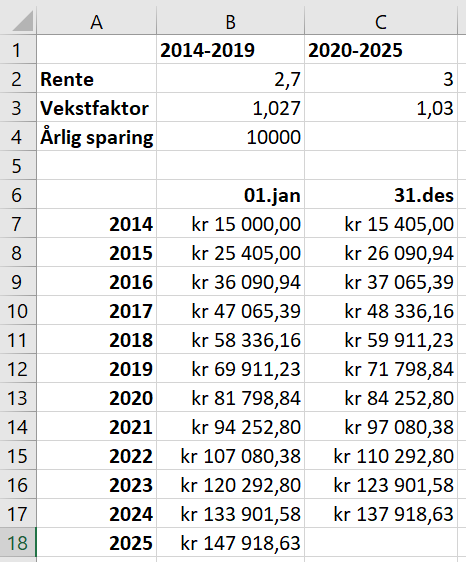
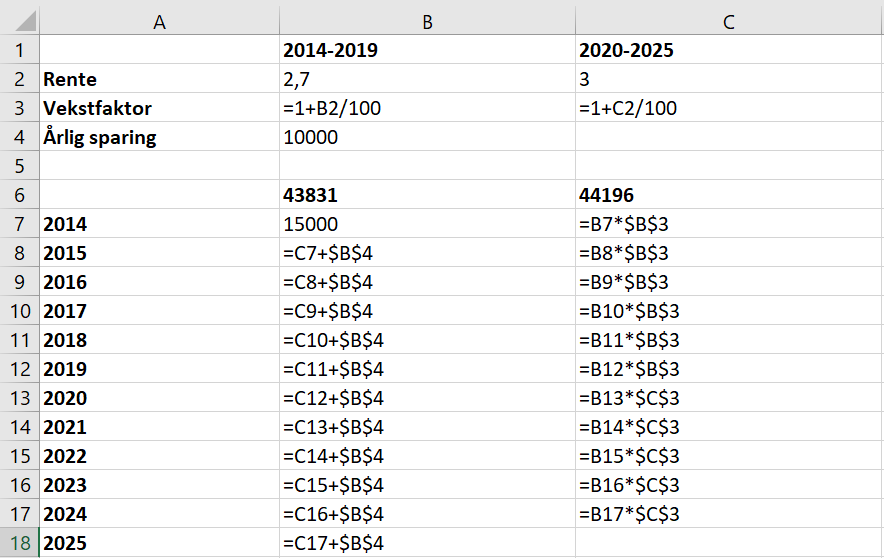
Lager regneark i Excel for å finne beløpet 1. januar 2020. Prøver meg frem til riktig rente i celle B1.
Rentesatsen denne perioden var 2,7%.
b)
Elin vil ha 149 918,63 kroner på kontoen rett etter at hun har satt inn 10 000 kr første januar 2025.
Oppgave 5
a)
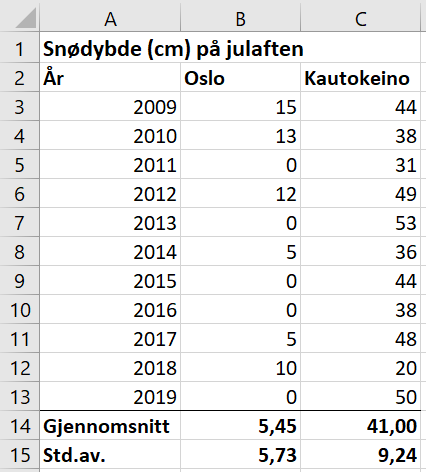
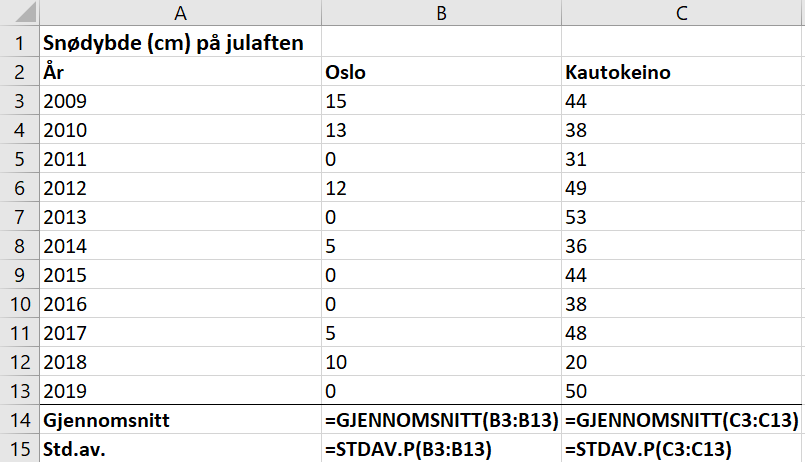
Bruker Excel.
Gjennomsnittlig snødybde på julaften i Oslo de 11 siste årene er 5,45 cm. Standardavviket er 5,73 cm.
Gjennomsnittlig snødybde på julaften i Kautokeino de 11 siste årene er 41 cm. Standardavviket er 9,24 cm.
b)
Påstanden er ikke riktig. Standardavviket sier noe om spredningen i tallmaterialet. Vi kan ha et datamateriale med høyt gjennomsnitt, men med mange tilnærmet like verdier; da vil standardavviket være lite selv om gjennomsnittet er høyt. Omvendt kan det være et datamateriale med mange veldig forskjellige verdier, som gir et høyt standardavvik uavhengig av gjennomsnittet.
Oppgave 6
a)
Bruker Geogebra, legger inn dataene i regnearket, og bruker "regresjonsanalyse".
Jeg velger en potensfunksjon som modell. Denne passer godt med punktene og flater ut etter hvert slik Svein antar. Modellen for antall innbyggere x år etter 1980 er $f(x) = 2033\cdot x^{0,2583}$
b)
Det vil være 5585 innbyggere i boliområdet i 2030 (x=50) ifølge modellen (se "symbolsk utregning" nederst på skjermbildet i oppgave a). Dette stemmer godt med Sveins antakelse om at antall innbyggere vil øke, men at økningen vil avta.
Oppgave 7
a)
Avtale 1: $y=1200\,kr\cdot 28 + 22000\,kr = 55600\,kr$
Avtale 2: $y=600\,kr \cdot 28 + 28000 \, kr= 44800\,kr$
Avtale 3: $y=200\,kr\cdot 28 + 50000\,kr = 55600\,kr$
b)
Bruker CAS i Geogebra:
Med avtale 1 kan kunden leie leiligheten i 25 døgn før den totale prisen overstiger 53 000 kroner. For avtale 2 er det 41 døgn, og for avtale 3 er det 15 døgn.
c)
Bruker Geogebra og tegner grafen til funksjonene.
Avtale 1 lønner seg frem til 10 døgn leie, Avtale 2 lønner seg fra 10 til 55 døgn leie, og avtale 3 lønner seg fra 55 døgn leie.
Oppgave 8
a)
Ser på diagrammet for maksimumstemperaturen i Oslo hvert døgn i januar 2020.
Medianen er ca. $5,6^{\circ}C$. Det er representert ved den vannrette streket i den grønne boksen. Jeg vet dette fra å ha sammenlignet med diagrammet for Trondheim, hvor jeg vet at medianen er $6^{\circ}C$.
Gjennomsnittet er ca. $5^{\circ}C$. Det er representert ved krysset i den grønne boksen.
Variasjonsbredden er ca. $9^{\circ}C-1,5^{\circ}C=7,5^{\circ}C$. Det er avstanden mellom største og minste verdi på diagrammet.
Kvartilbredden er ca. $6,9^{\circ}C-3,7^{\circ}C=3,2^{\circ}C$. Det er avstanden mellom største og minste verdi på den grønne boksen (altså 3. og 1. kvartil).
b)
Vi ser at 1. kvartil på begge diagrammene er på ca. $3,6^{\circ}C$. Det vil si at en fjerdedel av dagene i januar hadde en maksimumstemperatur på $3,6^{\circ}C$ eller lavere. En fjerdedel av 31 dager er nesten 8 dager.