Forskjell mellom versjoner av «2P 2016 høst LØSNING»
(→c)) |
|||
| (44 mellomliggende revisjoner av 5 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
| + | *[https://goo.gl/32tVw8 Link til løsningsforslag (videoer)] fra Joes. | ||
| + | |||
| + | |||
==DEL EN== | ==DEL EN== | ||
| Linje 5: | Linje 8: | ||
26,3 millioner = 26 300 000 = $2,63 \cdot 10^7$ | 26,3 millioner = 26 300 000 = $2,63 \cdot 10^7$ | ||
| − | $16,5 \cdot 10^{-8} = 1,65 \cdot 10^{- | + | $16,5 \cdot 10^{-8} = 1,65 \cdot 10^{-7}$ |
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 57: | Linje 60: | ||
$f(t)=0 \\ -500t +8500 =0 \\ - 500t= -8500 \\ t= 17$ | $f(t)=0 \\ -500t +8500 =0 \\ - 500t= -8500 \\ t= 17$ | ||
| − | I følge modellen vil det ikke være flere dyr igjen i | + | I følge modellen vil det ikke være flere dyr igjen etter 17 år, dvs i år 2010 + 17 = 2027. |
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 94: | Linje 97: | ||
|} | |} | ||
| − | Siden den relative frekvensen i første | + | Siden den relative frekvensen i første intervall er 0,05, er det det samme som 1 av 20. Derfor frekvens 1 i første intervall. Kumulativ i andre intervall er 6, da må frekvensen i dette intervallet være 5. 8/20 er 0,40 og kumulativ frekv. i intervall tre blir da 14. |
===b)=== | ===b)=== | ||
| Linje 128: | Linje 131: | ||
| − | Forutsetter at | + | Forutsetter at datamaterialet fordeler seg jevnt innen hver klasse. |
| − | Gjennomsnitt: $ \frac {2,5 \cdot 4 + 7, | + | Gjennomsnitt: $ \frac {2,5 \cdot 4 + 7,5 \cdot 12 + 12,5 \cdot 10 + 22,5 \cdot 4}{30} = 10,5$ |
Gjennomsnittet er 10,5 poeng. | Gjennomsnittet er 10,5 poeng. | ||
| Linje 147: | Linje 150: | ||
B = 2 Løper, gir brattere stigningstall enn A. Venter. Går tilbake. Nærmer seg saktere enn Eline i A som løper tilbake | B = 2 Løper, gir brattere stigningstall enn A. Venter. Går tilbake. Nærmer seg saktere enn Eline i A som løper tilbake | ||
| − | C = 4 Padling i motvind gir konstant fart. vinden | + | C = 4 Padling i motvind gir konstant fart. vinden stilner, farten og derved også avstanden til hjemmet øker raskere. Hun kom aldri tilbake.... |
D = 1 Beveger seg fram og tilbake uten pause. | D = 1 Beveger seg fram og tilbake uten pause. | ||
| Linje 162: | Linje 165: | ||
===a)=== | ===a)=== | ||
| + | 2,5 % økning gir en vekstfart på 1,025. | ||
$6500000 \cdot 1,025^8= 7919619$ | $6500000 \cdot 1,025^8= 7919619$ | ||
| Linje 170: | Linje 174: | ||
===b)=== | ===b)=== | ||
| − | $x \cdot 1,025^8 = 6500000 \\ x = 6500000 | + | $x \cdot 1,025^8 = 6500000 \\ x = \frac{6500000}{1,025^{8}} \\ x= 5334852 $ |
Eiendommen hadde en verdi på ca 5,3 millioner for åtte år siden. | Eiendommen hadde en verdi på ca 5,3 millioner for åtte år siden. | ||
| Linje 209: | Linje 213: | ||
===a)=== | ===a)=== | ||
| + | [[File:2p-h2016-2-4a.png]] | ||
| + | |||
| + | Gjennomsnittet er 18,6 og median er 20. | ||
===b)=== | ===b)=== | ||
| + | 1: $\frac{18,6}{20} = 0,93$ Riktig | ||
| + | |||
| + | 2: $\frac{20}{18,6} = 1,0753$ Riktig | ||
| + | |||
| + | Begge påstandene er riktige. | ||
===c)=== | ===c)=== | ||
| + | |||
| + | Standardavviket er 8,5, se figur i a. | ||
===d)=== | ===d)=== | ||
| + | |||
| + | Gjennomsnittet i 2B er det samme som i 2A, men standardavviket er mindre, det vil si en tettere samling av poeng rundt gjennomsnittet. Det er trolig at man finner de flinkeste elevene og de svakeste elevene i 2A. | ||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 222: | Linje 238: | ||
===a)=== | ===a)=== | ||
| + | [[File:2p-h2016-2-5ab.png]] | ||
| + | |||
| + | |||
| + | Modell: $f(t)= 0,55\cdot 0,9^t$ | ||
| + | |||
| + | Det betyr at konsentrasjonen er 0,55 mikrogram per milliliter når du inntar tabletten ( slik er det selvsagt ikke, det tar litt tid, men dette er en matematisk modell...). Virkestoffet nedbrytes med 10% per time. | ||
===b)=== | ===b)=== | ||
| + | Fra Figuren i a ser man at det er $0,2 \mu g/mL$ etter 10 timer. | ||
| + | |||
| + | ===c)=== | ||
| + | Her forutsetter vi at kroppen bryter ned 10% per time også med en høyere konsentrasjon enn den i a). | ||
| − | === | + | Tablett 1: $0,55 \cdot 0,905^{30} = 0,0275$ <br> |
| + | Tablett 2 : $0,55 \cdot 0,905^{18} = 0,0912$<br> | ||
| + | Tablett 3 : $0,55 \cdot 0,905^{6} = 0,03021$ | ||
| + | |||
| + | Summen av disse blir 0,421 $\mu g$. | ||
==Oppgave 6== | ==Oppgave 6== | ||
| + | |||
| + | [[File:2p-h2016-2-6.png]] | ||
| + | |||
| + | [[File:2p-h2016-2-62.png]] | ||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 235: | Linje 269: | ||
===a)=== | ===a)=== | ||
| + | |||
| + | [[File:2p-h2016-2-7a.png]] | ||
| + | |||
| + | |||
| + | Figur Nummer fire trenger 38 klosser, og figur fem trenger 62 klosser. Se figur. | ||
| + | |||
| + | Dersom du velger å tegne figurene og telle ruter, er det like greit. | ||
===b)=== | ===b)=== | ||
| − | Figuren består av et "hode" med to "ører". Hodet har høyde n og bredde n+1. Antall klosser i hodet blir da $n(n+1)= n^2+ n$. Ørene er kvadrater med sider (n-1). Vi får da $n^2+n + 2(n-1)^2 = n^2+n +2(n^2-2n+1)= 3n^2-3n+ | + | Figuren består av et "hode" med to "ører". Hodet har høyde n og bredde n+1. Antall klosser i hodet blir da $n(n+1)= n^2+ n$. Ørene er kvadrater med sider (n-1). Vi får da $n^2+n + 2(n-1)^2 = n^2+n +2(n^2-2n+1)= 3n^2-3n+2$. |
| − | Dersom du synes at det er | + | Dersom du synes at det er vanskelig å finne denne sammenhengen legger du figurnummer og tilhørende antall ruter inn i regnearket på geogebra og utfører regresjon. |
===c)=== | ===c)=== | ||
| − | Man kan løse likningen $3n^2-3n+ | + | Man kan løse likningen $3n^2-3n+2 = 1000 \\3n^2-3n - 998 =0$ |
| + | |||
| + | [[File:2p-h2016-2-7c.png]] | ||
| + | |||
| + | |||
| + | Det betyr at man kan lage figur nr 18. Men spørsmålet var hvor mange av de 1000 klossene som blir igjen. | ||
| + | |||
| + | $3 \cdot 18^2 -3 \cdot 18 +2 = 920$ | ||
| + | |||
| + | For Figur nr 18 trengs det 920 klosser. Da blir det 80 igjen. | ||
Nåværende revisjon fra 28. sep. 2017 kl. 15:47
- Link til løsningsforslag (videoer) fra Joes.
DEL EN
Oppgave 1
26,3 millioner = 26 300 000 = $2,63 \cdot 10^7$
$16,5 \cdot 10^{-8} = 1,65 \cdot 10^{-7}$
Oppgave 2
$ \frac{3,5\cdot 10^8}{7,0 \cdot 10^5 \cdot 0,5 \cdot 10^6} = \frac{3,5}{7 \cdot 0,5} \cdot 10^{8-5-6}= 1,0 \cdot 10^{-3} = 0,001 $
Oppgave 3
$\frac{135}{135 + 115} = \frac{135}{250} = \frac{270}{500} = \frac {540}{1000} = \frac{54}{100} = 54$ %.
Det er 54% jenter på skolen.
Oppgave 4
Butikk A: $1,1 \cdot 0,9$
Butikk B: $0,9 \cdot 1,1$
Prisen er den samme i begge butikkene ( Rekkefølgen av faktorene har ikke betydning).
Oppgave 5
$1024 = 2^{10}$
$ \frac {2^{10}}{2^{7}} = 2^{10-7} = 2^3 =8$
Etter 7 uker har du 8 kroner igjen.
Oppgave 6
a)
Synker med ca. 2500 dyr på 5 år dvs et stigningstall på -500.
$f(t)= -500t + 8500$
b)
$f(8)= -500 \cdot 8 + 8500 = 4500$
I 2018 vil det være ca 4500 dyr igjen, i følge modellen.
c)
$f(t)=0 \\ -500t +8500 =0 \\ - 500t= -8500 \\ t= 17$
I følge modellen vil det ikke være flere dyr igjen etter 17 år, dvs i år 2010 + 17 = 2027.
Oppgave 7
a)
| Klasse (ant. kunder) | Frekvens | Relativ frekvens | Kumulativ frekvens |
| [0,50> | 1 | 0,05 | 1 |
| [50, 100> | 5 | 0,25 | 6 |
| [100, 150> | 8 | 0,40 | 14 |
| [150, 200> | 6 | 0,30 | 20 |
Siden den relative frekvensen i første intervall er 0,05, er det det samme som 1 av 20. Derfor frekvens 1 i første intervall. Kumulativ i andre intervall er 6, da må frekvensen i dette intervallet være 5. 8/20 er 0,40 og kumulativ frekv. i intervall tre blir da 14.
b)
Det mangler en verdi i intervallet [ 0, 50>. Dette kan for eksempel være 42.
Det mangler to verdier i intervallet [ 150, 200>, Disse kan begge være 170.
Oppgave 8
a)
$V(x)= 250000 \cdot 0,9^x$
250000 - kjøpesum bil
0,9 - vekstfaktor som forteller at den taper seg i verdi med 10% per år (1 - 0,1 = 0,9).
b)
$V(1) = 250000 \cdot 0,9 = 225000$
Bilen vil i følge modellen ha en verdi på ca. 225 000 kroner.
Oppgave 9
a)
Forutsetter at datamaterialet fordeler seg jevnt innen hver klasse.
Gjennomsnitt: $ \frac {2,5 \cdot 4 + 7,5 \cdot 12 + 12,5 \cdot 10 + 22,5 \cdot 4}{30} = 10,5$
Gjennomsnittet er 10,5 poeng.
b)
Går man etter gjennomsnittet var han i den nedre halvdelen.
Median er nr. 15 og 16. Vi ser at begge disse verdiene befinner seg i mengden [ 5, 10>. Så Per bør holde seg til medianen når han legger fram sin påstand.
Oppgave 10
A = 3 Hun går, dvs. fjerner seg sakte fra hjemmet.
B = 2 Løper, gir brattere stigningstall enn A. Venter. Går tilbake. Nærmer seg saktere enn Eline i A som løper tilbake
C = 4 Padling i motvind gir konstant fart. vinden stilner, farten og derved også avstanden til hjemmet øker raskere. Hun kom aldri tilbake....
D = 1 Beveger seg fram og tilbake uten pause.
DEL TO
Oppgave 1
Oppgave 2
a)
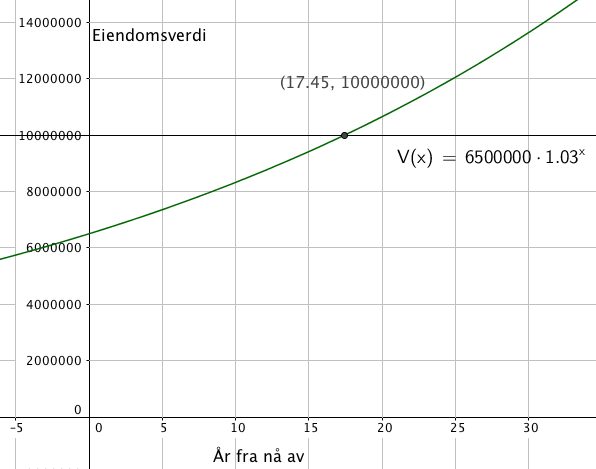
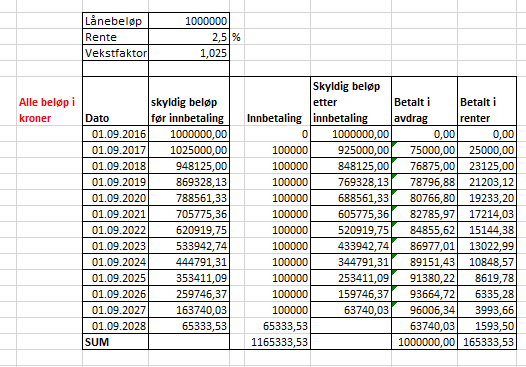
2,5 % økning gir en vekstfart på 1,025.
$6500000 \cdot 1,025^8= 7919619$
Eiendommen vil ha en verdi på ca 7,92 millioner.
b)
$x \cdot 1,025^8 = 6500000 \\ x = \frac{6500000}{1,025^{8}} \\ x= 5334852 $
Eiendommen hadde en verdi på ca 5,3 millioner for åtte år siden.
c)
Fra Figuren ser man at det tar ca 17,5 år før eiendommen har en verdi over 10 000 000 kroner.
Oppgave 3
a)
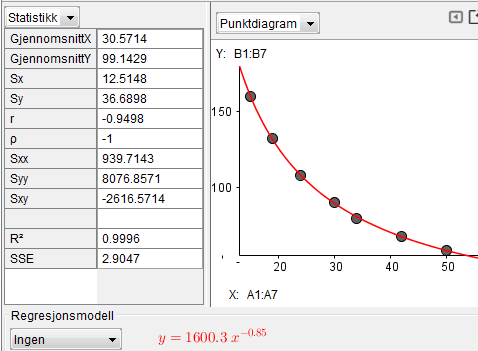
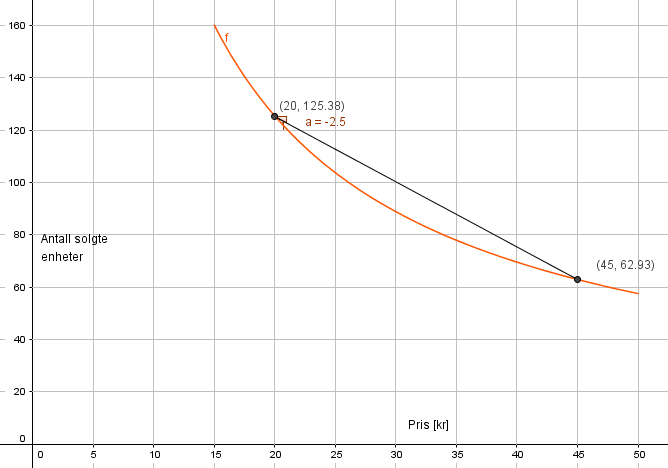
Kvadratet av regresjonskoefisienten: $R^2 =0,9996$, altså nesten 1,0 betyr at tilnærmingen er god. Du kan også se at punktene ligger på grafen.
b)
c)
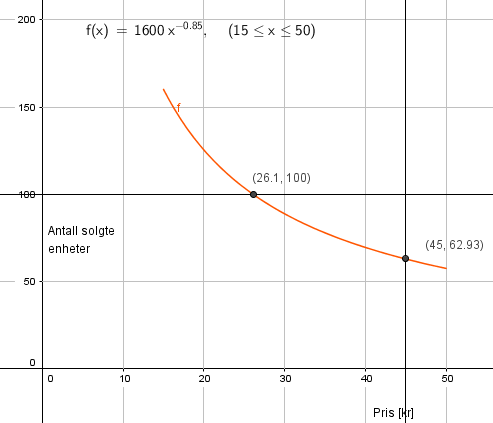
Dersom prisen er 45 kroner selges det 63 enheter. Se graf i b.
d)
Når det selges 100 enheter er prisen 26 kroner. Se graf i b.
e)
Dersom man øker prisen fra 20 til maks 45 kroner, vil antall solgte enheter i gjennomsnitt minke med 2,5 enheter for hver krone man øker prisen.
Oppgave 4
a)
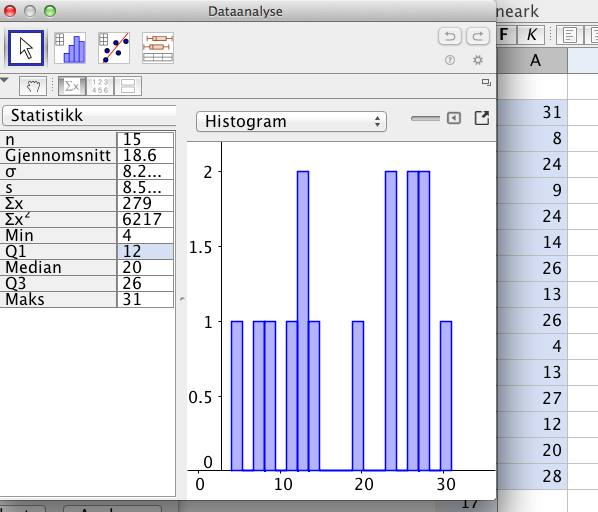
Gjennomsnittet er 18,6 og median er 20.
b)
1: $\frac{18,6}{20} = 0,93$ Riktig
2: $\frac{20}{18,6} = 1,0753$ Riktig
Begge påstandene er riktige.
c)
Standardavviket er 8,5, se figur i a.
d)
Gjennomsnittet i 2B er det samme som i 2A, men standardavviket er mindre, det vil si en tettere samling av poeng rundt gjennomsnittet. Det er trolig at man finner de flinkeste elevene og de svakeste elevene i 2A.
Oppgave 5
a)
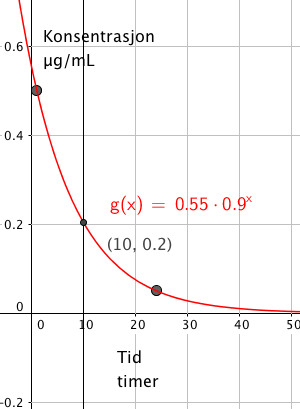
Modell: $f(t)= 0,55\cdot 0,9^t$
Det betyr at konsentrasjonen er 0,55 mikrogram per milliliter når du inntar tabletten ( slik er det selvsagt ikke, det tar litt tid, men dette er en matematisk modell...). Virkestoffet nedbrytes med 10% per time.
b)
Fra Figuren i a ser man at det er $0,2 \mu g/mL$ etter 10 timer.
c)
Her forutsetter vi at kroppen bryter ned 10% per time også med en høyere konsentrasjon enn den i a).
Tablett 1: $0,55 \cdot 0,905^{30} = 0,0275$
Tablett 2 : $0,55 \cdot 0,905^{18} = 0,0912$
Tablett 3 : $0,55 \cdot 0,905^{6} = 0,03021$
Summen av disse blir 0,421 $\mu g$.
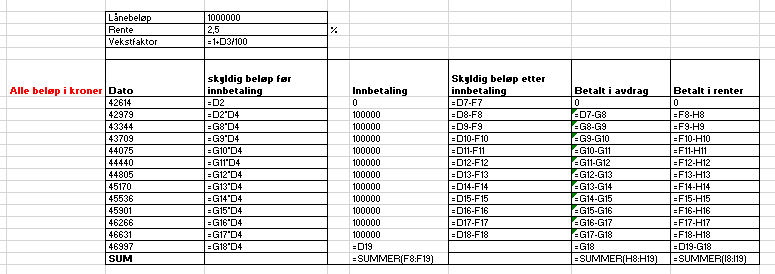
Oppgave 6
Oppgave 7
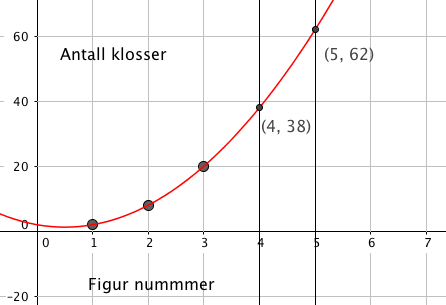
a)
Figur Nummer fire trenger 38 klosser, og figur fem trenger 62 klosser. Se figur.
Dersom du velger å tegne figurene og telle ruter, er det like greit.
b)
Figuren består av et "hode" med to "ører". Hodet har høyde n og bredde n+1. Antall klosser i hodet blir da $n(n+1)= n^2+ n$. Ørene er kvadrater med sider (n-1). Vi får da $n^2+n + 2(n-1)^2 = n^2+n +2(n^2-2n+1)= 3n^2-3n+2$.
Dersom du synes at det er vanskelig å finne denne sammenhengen legger du figurnummer og tilhørende antall ruter inn i regnearket på geogebra og utfører regresjon.
c)
Man kan løse likningen $3n^2-3n+2 = 1000 \\3n^2-3n - 998 =0$
Det betyr at man kan lage figur nr 18. Men spørsmålet var hvor mange av de 1000 klossene som blir igjen.
$3 \cdot 18^2 -3 \cdot 18 +2 = 920$
For Figur nr 18 trengs det 920 klosser. Da blir det 80 igjen.