1T eksempeloppgave 2015 vår LØSNING

Oppgave 1

a)

$8,20 \cdot 10^9 \cdot 1,50 \cdot 10^{-3}= \\ 12,30 \cdot 10^{9-3} = \\ 1,23 \cdot 10^7$

b)

$\frac{(a^2)^4 \cdot ( \frac ba)^2}{a^3 \cdot b^{-2}} = \frac{a^8 \cdot \frac{b^2}{a^2}}{a^3b^{-3}} = a^{8-5}b^4 = a^3b^4$

Oppgave 2

a)

$(a+b)^2 - (a-b)^2 = \\ a^2+2ab + b^2 - (a^2-2ab+b^2) = \\ a^2+2ab + b^2 - a^2 + 2ab -b^2 = \\ 4ab$

Oppgave 3

a)

$g(x)= \frac 13x^3-x^2-3x+4 \quad D_g = \R \\ g'(x)= x^2-2x-3 \\ g'(1)= 1-2-3 =-4$

Den momentane vekstfarten i x=1 er -4.

b)

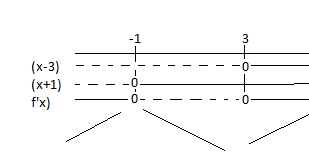
$g'(x)= 0 \\ x^2-2x-3 =0 \\ x=-1 \vee x=3$

Fortegnsskjema:

$g(-1)= - \frac 13 -1 +3+4 = 5 \frac23 \\ g(3)= 9-9-9+4= 5$

Maksimumspunkt i $(-1, \frac{17}{3})$

Minimumspunkt i $(3, 5)$

Oppgave 4

a)

Et kvadrat med omkrets 16 har sider lik 4 og et areal på 16.

En sirkel med omkrets 16 har radius $\frac{8}{\pi}$. Arealet blir da

$A= \pi r^2 \\ A= \pi ( \frac {8}{\pi})^2 \\ A= \frac{64}{\pi}$

som er et større areal enn 16. Sirkelen har størst areal.

b)

$A= \frac{(a+b)}{2} \cdot h \\ h = \frac{2A}{(a+b)}$

c)

De parallelle sidene er x og x + 2 cm. lange.

$18= \frac{x+x+2}{2} \cdot 3 \\ 3x+3 =18 \\ x=5$

Den ene siden er 5 cm lang, den andre 7 cm lang.

Oppgave 5

a)

b)

$A= \frac 12 ab SinC \\ sin 140^{\circ}> sin30^{\circ}$

$\triangle ABC$ har størst areal.

Oppgave 6

a)

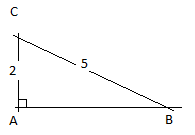
$y=ax+b \\ a = \frac{\Delta y}{\Delta x} = \frac{4-2}{2-1} = 2 \\ y= 2x+b \\ 2= 2\cdot 1+ b \\ b = 0 \\ y=2x$

b)

$f(x)= x^2+4 \\ f'x) = \lim_{\Delta x \rightarrow 0} \frac{f(x+ \Delta x) - f(x)}{\Delta x} = \\ \lim_{\Delta x \rightarrow 0} \frac{(x+ \Delta x)^2 +4 - x^2 -4}{\Delta x} = \\ \lim_{\Delta x \rightarrow 0} \frac{x^2 + 2x \Delta x + (\Delta x)^2 -x^2-4}{\Delta x} $

Oppgave 10

a)

Finner arealet av OAB og trekker fra arealet av de mindre trekantene OQP, QBM og MAP.

Areal $triangle PQM $ $ A =16-( \frac{x^2}{2} + \frac{(8-x)2}{2} + \frac{(4-x)4}{2}) \\ A= 16 - \frac{x^2}{2}-8+x-8+2x \\ A= - \frac{x^2}{2} + 3x$

Som skulle vises. (x kan ikke være mindre enn null, eller større enn fire).

b)

$T'(x) = -x + 3 \\ T'(x)=0 \\ x=3 $

Vi ser av fortegnet til andregradsleddet i T at x = 3 gir et maksimumspunkt. Arealtet av trekanten PQM er altså størst når x=3.

T(3) = 4,5