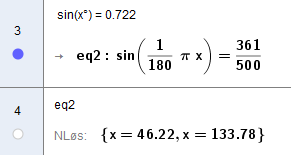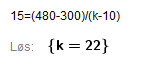1T 2020 vår eksempeloppgave LØSNING

Diskusjon av denne oppgaven på matteprat

Løsning som docx av Kristian Saug

Løsning som pdf av Kristian Saug

TYPE 1 OPPGAVER (oppgave 1 - 6)

Disse oppgavene blir maskinrettet og det er kun svaret som har betydning. Hvordan du kommer fram til riktig svar blir ikke vurdert. Vær nøye når du taster inn svaret siden det er det eneste som betyr noe. Slurvefeil her straffes hardt. Type en oppgavene blir trolig vurdert til en lavere poengsum enn type 2 og 3 oppgaver.

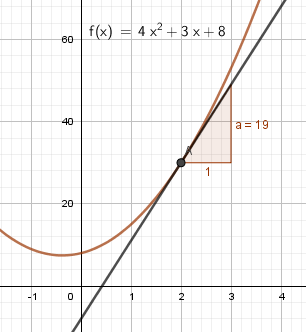
Oppgave 1

Den momentane veksten når x er to, er 19.

Dersom du i stede for grafisk løsning ønsker å bruke CAS kan du gjøre det slik:

Svaret blir fortsatt 19.

Dersom du er trygg på derivasjon er det nok mye raskere å derivere med blyant og papir, sette inn f ' (2) og skrive 19 rett inn på PC.

Oppgave 2

Sinus til en vinkel kan ha verdier mellom -1 og 1. Dersom man får 2 til svar har man regnet feil.

Oppgave 3

I enhetssirkelen er x koordinaten til cosinus til vinkelen og y koordinaten er sinus til vinkelen.

Vi får

Vinkel u ligger i første kvadrant og er 46,22 grader.

Her er det trolig raskere å bruke en vanlig kalkulator til utregningen, Hvor mange desimaler maskinen som retter forventer, regner jeg med at UDIR vil opplyse om.

Vinkel v speiler u om x aksen og ligger i 4 kvadrant . Den er 360 - u, altså 313,78 grader.

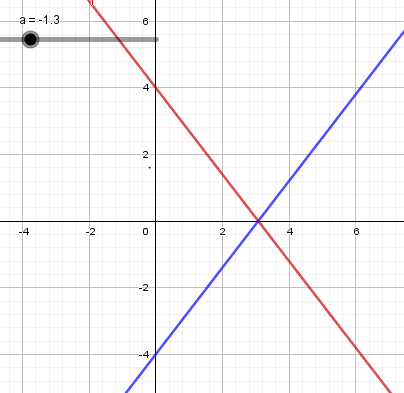
Oppgave 4

$ x = - \frac{4}{a}$. y er alltid null pga. symmetrien rundt x aksen. Men, to svar, ingen begrunnelse nødvendig.

Oppgave 6

Stigningstallet til den rette linjen er 15, det er hva hun tjener per solgte bok. Setter 15 lik endring i y verdi delt på endring i x verdi og får k = 22.

TYPE 2 OPPGAVER

Her skal du begrunne dine valg, skrive utfyllende svar og vise utregning. Alle oppgavene leveres samlet i en fil. Disse oppgavene vektlegges trolig mer enn type 1 oppgaver.

Oppgave 7

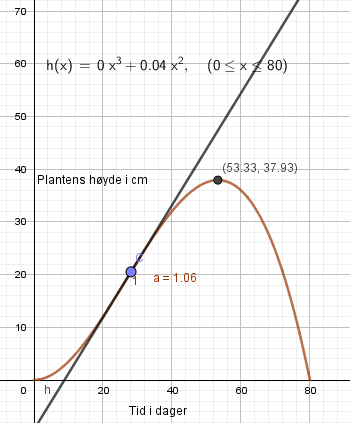
a)

Planten vokser lite de første dagene, men veksten er økende. Fra ca dag 15/ 20 til dag 40 har planten en tilnærmet lineær vekst. Den vokser da med ca 1,1 cm per dag. Etter dag 40 flater veksten ut og den ser ut til å oppnå full høyde som er ca 38 cm, etter ca 53 dager. Dette er jo en modell så man kan forvente avvik fra plante til plante.

b)

Det er lite trolig at planten krymper kontrollert umiddelbart etter å ha nådd maksimal høyde. Man kan anta at modellens gyldighetsområde er fra null til femti dager, grovt regnet.

Oppgave 10

Oppgave 13

Her tenkte jeg slik:

dersom a = r, må b være lik r^5. I tillegg burde man også få med i svaret at koordinatet for skjæringspunktet gir (x, x^3).