Forskjell mellom versjoner av «1T 2013 høst LØSNING»
(→a)) |
|||
| (10 mellomliggende revisjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
| − | [http://matematikk.net/ | + | {{EksLenker|1= |
| − | + | *[http://matematikk.net/res/eksamen/1T/1T_H13.pdf Oppgaven som pdf] | |
| − | [http://matematikk.net/matteprat/viewtopic.php?f=13&t=36353 Diskusjon av denne oppgaven på matteprat] | + | *[http://matematikk.net/matteprat/viewtopic.php?f=13&t=36353 Diskusjon av denne oppgaven på matteprat] |
| + | *[http://www.matematikk.net/res/eksamen/1T/sensur/2013H_Vurderingsskjema_MAT1013_Matematikk_1T_H13.pdf Vurderingsskjema] | ||
| + | *[http://www.matematikk.net/res/eksamen/1T/sensur/2013H_Sensorveiledning_MAT1013_Matematikk_1T_H13.pdf Sensorveiledning] | ||
| + | *[http://ndla.no/nb/node/138107?fag=54 Løsning fra NDLA] | ||
| + | }} | ||
==DEL EN== | ==DEL EN== | ||
| Linje 63: | Linje 67: | ||
==Oppgave 5:== | ==Oppgave 5:== | ||
| − | $ | + | $2\lg x-8=5\lg x+1 \\ -3\lg x =9 \\ \lg x =-3 \\ x = 10^{-3} = 0,001$ |
==Oppgave 6:== | ==Oppgave 6:== | ||
| Linje 145: | Linje 149: | ||
[[File:10-1t-h2013.png]] | [[File:10-1t-h2013.png]] | ||
| − | Bruker først | + | Bruker først Pytagoras på den rettvinklede trekanten til høyre, for å finne det ukjente katetet. |
| Linje 168: | Linje 172: | ||
$f ´(x)= 9x^2-96x+162 \\f´(x) = 0 \\ 9x^2-96x+162 = 0 \\ | $f ´(x)= 9x^2-96x+162 \\f´(x) = 0 \\ 9x^2-96x+162 = 0 \\ | ||
| − | x= \frac{ | + | x= \frac{96 \pm \sqrt{96^2 - 4 \cdot 9 \cdot 162}}{18} \\ |
| − | x=2,1 \vee x=8, | + | x=2,1 \vee x=8,5$ |
| − | Nå vet vi fra oppgave a og b at 2,1 er et maksimum og 8, | + | Nå vet vi fra oppgave a og b at 2,1 er et maksimum og 8,5 et minimum. Dersom man liker å regne ser man at den deriverte er negativ før 8,6 , og positiv etter 8,6. Det betyr at 8,6 er et minimumspunkt. |
===d)=== | ===d)=== | ||
| Linje 178: | Linje 182: | ||
| − | f(5) forteller oss at bestanden i 2005 var på 285 tonn. den deriverte forteller oss at | + | f(5) forteller oss at bestanden i 2005 var på 285 tonn. den deriverte forteller oss at nedgangen per år, slik den sees i 2005, er på 93 tonn. |
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 195: | Linje 199: | ||
==Oppgave 3== | ==Oppgave 3== | ||
| − | Sannsynligheten p for at en | + | Sannsynligheten p for at en syklist sykler uten lys er 0,2. |
$P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k}$ | $P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k}$ | ||
| Linje 205: | Linje 209: | ||
$P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k} \\ P(X=0)= \binom{10}{0} 0,2^0 \cdot 0,8^{10} = 0,107$ | $P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k} \\ P(X=0)= \binom{10}{0} 0,2^0 \cdot 0,8^{10} = 0,107$ | ||
| − | Minst en | + | Minst en sykler uten lys i mørket er da 1 - 0,107 = 0,893 = 89,3%. |
===b)=== | ===b)=== | ||
| Linje 218: | Linje 222: | ||
$P(X=3)= \binom{10}{3} 0,2^3 \cdot 0,8^{7} = 0,2013$ | $P(X=3)= \binom{10}{3} 0,2^3 \cdot 0,8^{7} = 0,2013$ | ||
| − | Det er ca 20% | + | Det er ca 20% sannsynlig at tre syklister sykler uten lys. |
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 248: | Linje 252: | ||
AB er 8,0cm. Både AC og AD er 5,0 cm. Begge trekantene er $17,5cm^2$ (bommet med en hundredel på den ene :-)). | AB er 8,0cm. Både AC og AD er 5,0 cm. Begge trekantene er $17,5cm^2$ (bommet med en hundredel på den ene :-)). | ||
| − | I dagens dataverden der matematikk får stadig mindre rom i skolen er vel oppgaven å betrakte som løst. Men, dersom man ønsker en analytisk tilnærming kan man gjøre slik: | + | I dagens dataverden der matematikk får stadig mindre rom i skolen er vel oppgaven å betrakte som løst. Men, dersom man ønsker en mere analytisk tilnærming kan man gjøre slik: |
| − | $ | + | $ T= \frac 12 bc \sin A \\ \Downarrow \\ \sin A= \frac{2T}{bc} \\ \sin A= \frac{2 \cdot 17,5}{8 \cdot 5} \\ A= 61^{\circ} \vee A = 180^{\circ} -61^{\circ}= 119^{\circ} $ |
Vinkelen mellom den 8,0 cm lange siden og den 5,0cm lange siden er 61 grader eller 119 grader. | Vinkelen mellom den 8,0 cm lange siden og den 5,0cm lange siden er 61 grader eller 119 grader. | ||
Nåværende revisjon fra 22. nov. 2014 kl. 13:30
DEL EN
Oppgave 1:
$7,5 \cdot 10^{12} \cdot 4,0 \cdot 10^{-4} = 30 \cdot 10^{12+(-4)} = 30 \cdot 10^8 = 3,0 \cdot 10^9$
Oppgave 2:
a)
| Blå bukser | Svarte bukser | Total | |
|---|---|---|---|
| Bukser som passer | $3$ | $3 $ | $6$ |
| Bukser som ikke passer | $1$ | $3$ | $4$ |
| Total | $4$ | $6$ | $10$ |
b)
P (buksa passer) =$\frac {6}{10}$ = 60%
Det er 60% sjanse for at buksa passer.
c)
P ( blå bukse, gitt at den passer) = $\frac 36 = \frac 12 = $ 50%
Det er 50% sjanse for at buksa er blå, når vi vet at hun har trukket en bukse som passer.
Oppgave 3:
$\frac {2x^2-18}{x^2+6x+9} = \frac {2(x+3)(x-3)}{(x+3)(x+3)} = \frac{2(x-3)}{x+3}$
Oppgave 4:
$ \frac{\sqrt 2 \cdot 2^0 \cdot 2^{-1}}{8^{\frac12} \cdot 2^{-2}} = \frac{2^{\frac 12} \cdot 2^{-1}}{2^{\frac 32}\cdot 2^{-2}} = \\ 2^{\frac12 -1-\frac32 + 2} = 2^0=1 $
Oppgave 5:
$2\lg x-8=5\lg x+1 \\ -3\lg x =9 \\ \lg x =-3 \\ x = 10^{-3} = 0,001$
Oppgave 6:
Rett linje: y = ax + b
stigningstall: $a = \frac{\Delta y}{\Delta x} = \frac{5-2}{3-1} = \frac 32$
Bruker dette sammen med første punkt og får:
$y=ax + b \\ 2= \frac 32 \cdot 1 + b \\ b= \frac 12$
Dvs:
$y = \frac 32x + \frac 12$
Oppgave 7:
$ -x+y =2 \\ -2x^2+y^2 =4 $
$ y =2 + x \\
-2x^2+(2+x)^2 =4 $
Finner x fra den nederste ligningen:
$4x-x^2 = 0\\ x(4-x) =0\\ x=0 \vee x=4$
Setter inn i -x+ y = 2 for å finne tilhørende y verdier.
Finner da at x = 0 gir y = 2 og x = 4 gir y = 6, så svarene er ( 0, 2) og (4, 6).
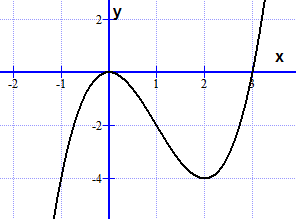
Oppgave 8:
a)
$f(x) = x^3-3x^2 \quad D_f = \R \\ f´(x) = 3x^2-6x \\ f´(x)=0 \\ x(3x-6)= 0 \\ x= 0 \vee x = 2$
Setter 0 og 2 inn i funksjonsuttrykket for å finne ekstremalpunkt:
$f(0)= 2 \wedge f(2)= -4 $
Vi har ekstremalpunktene ( 0, 0 ) og ( 2, -4 ).
f ´ ( -1) er positiv.
f ´( 1) er negativ og
f ´( 3) = er positiv. Det betyr at (0, 0) er et maksimumspunkt og ( 2, -4) er et minimumspunkt.
b)
Faktoriserer f(x):
$f(x) = x^3-3x^2 = x^2(x-3)$
Setter f(x) = 0 og får:
$f(x)=0 \\ x^2(x-3)=0 \\ x=0 \vee x =3$
Nullpunkter er (0, 0) og (3, 0).
c)
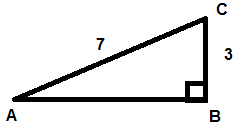
Oppgave 9:
Cosinus til en vinkel i en rettvinklet trekant er definert som hosliggende katet delt på hypotenusen. $ cos C = \frac 37$
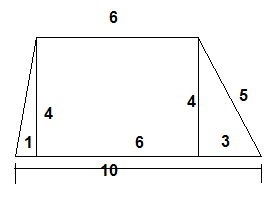
Oppgave 10:
Bruker først Pytagoras på den rettvinklede trekanten til høyre, for å finne det ukjente katetet.
Lengden av hypotenusen i den rettvinklede trekanten til venstre er $ \sqrt {4^2 + 1^2} = \sqrt {17}$ . omkretsen blir derved 10 + 5 + 6 + $ \sqrt{17} = 21 + \sqrt{17}$ .
DEL TO:
Oppgave 1
a)
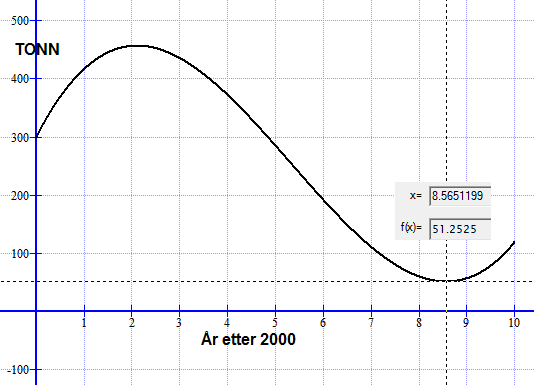
b)
Fiskebestanden var minst sommeren 2008, da var den i overkant av 51 tonn.
c)
$f(x) = 3x^3-48x^2+162x+300 \\ f ´(x)= 9x^2-96x+162$
Finner minimumspunktet ved å sette den deriverte lik null.
$f ´(x)= 9x^2-96x+162 \\f´(x) = 0 \\ 9x^2-96x+162 = 0 \\ x= \frac{96 \pm \sqrt{96^2 - 4 \cdot 9 \cdot 162}}{18} \\ x=2,1 \vee x=8,5$
Nå vet vi fra oppgave a og b at 2,1 er et maksimum og 8,5 et minimum. Dersom man liker å regne ser man at den deriverte er negativ før 8,6 , og positiv etter 8,6. Det betyr at 8,6 er et minimumspunkt.
d)
$f(x) = 3x^3-48x^2+162x +300 \\ f(5) = 3 \cdot 5^3-48 \cdot 5^2+162 \cdot 5 +300 = 285 \\ f ´(x)= 9x^2-96x+162 \\ f´(5)= 9\cdot 25 -96 \cdot 5 + 162= -93$
f(5) forteller oss at bestanden i 2005 var på 285 tonn. den deriverte forteller oss at nedgangen per år, slik den sees i 2005, er på 93 tonn.
Oppgave 2
a)
$f(x) = 20000 \cdot 0,92^x \\ f(1)= 20000 \cdot 0,92^1 = 18400 \\ f(10)=20000 \cdot 0,92^{10} = 8687,8$
Etter ett døgn er det 18400 liter igjen, og etter ti døgn er det 8687,8 liter igjen i dammen.
b)
$f(x)= 5000 \\ 20000 \cdot 0,92^x \\ 0,92^x = \frac 14 \\ x\cdot lg0,92 = lg0,25 \\ x= 16,6$
Det vil ta ça. 16,6 døgn før det er 5000 liter igjen i dammen.
Oppgave 3
Sannsynligheten p for at en syklist sykler uten lys er 0,2.
$P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k}$
a)
Ingen sykkler uten lys:
$P(X=k)= \binom{n}{k} p^k \cdot (1-p)^{n-k} \\ P(X=0)= \binom{10}{0} 0,2^0 \cdot 0,8^{10} = 0,107$
Minst en sykler uten lys i mørket er da 1 - 0,107 = 0,893 = 89,3%.
b)
Sannsynligheten for at nr, 1, nr. 4 og nr. 10 sykler uten lys. Her er bare en kombinasjon mulig:
$P(\text{1,4 og 10 uten lys}) = 0,2^3 \cdot 0,8^7 = 0,00167 \approx 0,2 \%$
c)
Tre av ti kjører uten lys:
$P(X=3)= \binom{10}{3} 0,2^3 \cdot 0,8^{7} = 0,2013$
Det er ca 20% sannsynlig at tre syklister sykler uten lys.
Oppgave 4
Hver av dem har så mange mynter:
Pål = x
Espen = 2x
Per = 6x
til sammen har de 198 mynter.
6x + 2x + x = 198
9x = 198
x = 22
Pål har 22 mynter, Espen har 44 mynter og Per har 132 mynter.
Oppgave 5
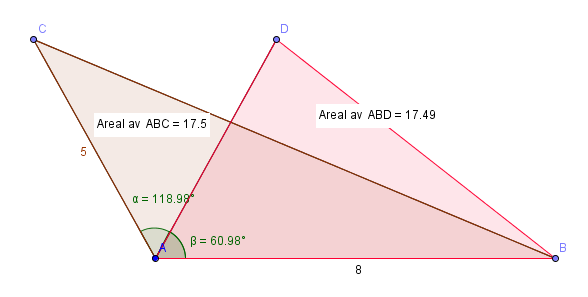
Trekantene kan se slik ut;
AB er 8,0cm. Både AC og AD er 5,0 cm. Begge trekantene er $17,5cm^2$ (bommet med en hundredel på den ene :-)).
I dagens dataverden der matematikk får stadig mindre rom i skolen er vel oppgaven å betrakte som løst. Men, dersom man ønsker en mere analytisk tilnærming kan man gjøre slik:
$ T= \frac 12 bc \sin A \\ \Downarrow \\ \sin A= \frac{2T}{bc} \\ \sin A= \frac{2 \cdot 17,5}{8 \cdot 5} \\ A= 61^{\circ} \vee A = 180^{\circ} -61^{\circ}= 119^{\circ} $
Vinkelen mellom den 8,0 cm lange siden og den 5,0cm lange siden er 61 grader eller 119 grader.
Oppgave 6
a))
Areal av trekanten ABE: $T_{ABE} = \frac 12 \cdot AE \cdot BE \cdot \sin 30^{\circ} = 9,0 m^2$
b)
Skal finne lengden av CE. Her er det bare å bruke cosinussettningen rett fram, alle størrelser er kjente:
$(CE)^2 = (ED)^2 + (CD)^2 - 2\cdot ED \cdot CD \cos 85,3^{\circ} \\ = 9m^2 +81m^2 - 2\cdot 3m \cdot 9m \cdot 0,0819 \\ = 90m^2 - 4,42 m^2 \\CE = 9,3m$
c)
Lengden av BC kan man finne ved å bruke sinussettningen, men vi må først finne vinkel ECB, for så å finne vinkel BEC som er motstående vinkel til siden BC.
$ \frac {\sin ECB}{6,0} = \frac{\sin 83,3^{\circ}}{9,3} \\ \sin ECB = 0,64 \\ \angle ECB = 39,8^{\circ}$
Da er vinkel BEC : 180 - 39,8- 83,3 = 56,9 grader.
Finner så siden BC:
$ \frac {\sin 56,9^{\circ}}{BC} = \frac{\sin 83,3^{\circ}}{9,3} \\ BC = 7,8$
BC er 7,8 meter lang.
Oppgave 7
a)
Bruker Pytagoras og finner at y = $\sqrt 5$, dvs. høyden av kjeglen er h = 3 + y = 3 + $\sqrt 5 \approx$ 5,24
b)
$V = \frac 13 \pi r^2h = \frac 13 \cdot \pi \cdot 4 \cdot 5,24 \approx 21,9 $
c)
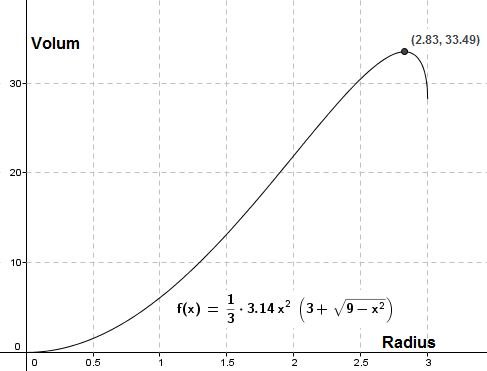
$V = \frac 13 \pi r^2h = \frac 13 \pi \cdot x^2 \cdot (3+y) = \frac 13 \pi \cdot x^2 \cdot (3+ \sqrt{3^2 - x^2} )=\frac 13 \pi \cdot x^2 \cdot (3+ \sqrt{9 - x^2}) $
d)
Man observerer at kjeglen har sitt største volum på 33,5 kubikk lengdeenheter. Da er radius 2,83 lengdeenheter. kjeglens flate er i den nedre halvkulen. Høyden er $h=3+ \sqrt{9-x^2} = 3 + \sqrt{9-2,83^2} = 4$. Høyden er 4 lengdeenheter.