1T 2010 vår LØSNING

Del 1

Oppgave 1

a)

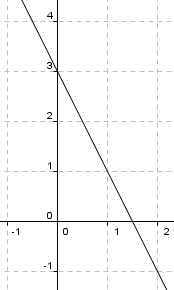
Nullpunkt ved regning:

<tex>f(x) = 0 \\ -2x+3 = 0 \\-2x= -3 \\x= \frac 32</tex>

Ved inspeksjon ser man at dette stemmer med grafen.

b)

<tex>x^2 + 8x = -15 \\ x^2 +8x + 15 =0 \\ x = \frac{-8 \pm \sqrt{8^2-4 \cdot 1 \cdot 15}}{2 \cdot1} \\x= \frac{-8 \pm 2}{2} \\ x = -5 \vee x=-3</tex>

c)

<tex>5 -2^4 \cdot(4-3)^3 \cdot 2^{-3}= \\ 5-16 \cdot 1^3 \cdot \frac 18 =\\ 5- \frac{16}{8} = 3</tex>

d)

<tex> \frac{4a^{\frac 13} \cdot a^{\frac 12}}{2a^{- \frac 16}} =\frac{2^2a^{\frac 13} \cdot a^{\frac 12}}{2a^{- \frac 16}} = 2^{2-1}a^{\frac 13 + \frac 12 -(- \frac 16)} = 2 a^{\frac 26 + \frac 36 + \frac 16} = 2a</tex>

e)

<tex>f(x)= -2x^3+8x+4 \\ f'(x) = -6x + 8 \\ f'(1) = -6+8=2 \\ f(1) = 10 \\ y= ax+b \\ y=2x+b \\punktet \quad (1,f(1)) \Rightarrow 10 = 2 + b \\ b = 8 \\ Likning \quad for \quad tangent: \quad y=2x+8</tex>

f)

Faktoriserer uttrykket ved hjelp av konjugatsetningen og regelen for faktorisering av fullstendig kvadrat, forkorter deretter uttrykket ved å stryke samme faktorer i teller og nevner:

<tex>\frac {x^2-9}{x^2+6x+9}=\frac {(x+3)\cdot (x-3)}{(x+3)(x+3)}=\frac {\cancel{(x+3)}\cdot (x-3)}{\cancel{(x+3)}(x+3)} =\frac {x-3}{x+3}</tex>

g)

<tex> \log(2x +4) = 3 \log 2 \Leftrightarrow \log (2x+4)= \log(2^3) \Leftrightarrow 2x+4=2^3 \Leftrightarrow 2x+4=8 \Leftrightarrow 2x=8-4 \Leftrightarrow 2x=4 \Leftrightarrow x= \frac 42 \Leftrightarrow x=2 </tex>

h)

1)

Sannsynligheten for at pilen peker enten på blått eller grønt felt når hjulet stopper er:

<tex> P=P(B)+P(Gr)=\frac 38 + \frac 28 = \frac 58=0,625 =62,5 \percent </tex>

2)

Sannsynligheten for at pilen peker en gang på gult felt og en gang på grønt felt når hjulet snurres to ganger, er:

<tex>P=P(Gul)\cdot P(Gr))=\frac 18 \cdot \frac 28= \frac {2\cdot 1}{8\cdot 8}=\frac 2{64}=\frac 1{32}=0,03125=3,125 \percent</tex>

i)

Oppgave 2

a)

b)

<tex> g(x) = ax^2+bx+c \\ g(0) = -4 \Rightarrow C= -4 \\ g(x) = ax^2+bx-4 \\ g(2)= 0 \Rightarrow 4a+2b-4=0 \\ g(-2) =0 \Rightarrow 4a-2b-4 =0 </tex>

Legger sammen de to likningene og får:

8a-8=0

a=1

Innsatt i 4a + 2b- 4 = 0

Gir b=0, funksjonsuttrykket blir da

<tex>g(x)= x^2-4</tex>

Del 2

Oppgave 3

a)

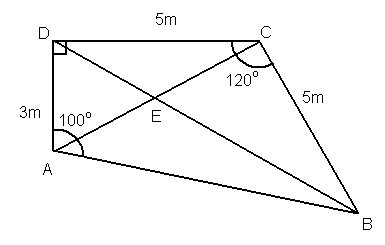
Siden trekant <tex>ACD</tex> er rettvinklet er det greit å finne lengden <tex>AC</tex> ved hjelp av Pytagoras setning:

<tex> AC^2=AD^2+CD^2 \Leftrightarrow AC=\sqrt{AD^2+CD^2} =\sqrt{(3,0 m)^2 + (5,0 m)^2}=\sqrt{9,0 m^2 + 25 m^2}=\sqrt{34 m^2} \approx 5,8 m</tex>

b)

Cosinussetningen:

<tex>BD^2 = (5m)^2 + (5m)^2 - 2 \cdot 5m \cdot 5m \cdot Cos 120^{\circ}= 75m^2 \\BD = 8,7m</tex>

c)

Areal trekant ACD: <tex>A= \frac {3,0m \cdot 5,0m}{2}= 7,5m^2</tex>

For å finne arealet av de tre andre trekantene trenger man å finne en del størrelser.

Bruker tangens og finner at:

Vinkel CAD = 59,04 grader

Vinkel DCA = 30,96 grader

Det fører til at

Vinkel BAE = 40,96 grader og

Vinkel ACB = 89,04 grader

Trekanten BCD er likebeint hvilket betyr at vinkel CBE = EDC = 30 grader.

Areal trekant BCD: <tex>A= \frac 12 \cdot 5m \cdot 5m \cdot sin 120^{\circ}= 10,825m^2</tex>

Areal trekant ABD: <tex>A = \frac 12 \cdot 3m \cdot \sqrt{75}m \cdot sin60^{\circ} = 11,25m^2</tex>

Areal trekant ABC: <tex>A = \frac 12 \cdot 5m \cdot 5,8m \cdot sin89^{\circ} = 14,5m^2</tex>

1)

OVE: ABD+BCD

2)

TOMMY: ABC+ACD

Oppgave 4

a)

Bruker fartsformelen <tex>s=vt</tex>, der <tex>s</tex> er strekningen Arne har syklet, <tex>v</tex> er farten han sykler med, og <tex>t</tex> er tiden han har brukt:

<tex>s=s_1+s_2=v_1 \cdot t_1 + v_2 \cdot t_2 = 12 \text{km/t} \cdot \frac {30 \text{min}}{60 \text{min}} + 18 \text{km/t} \cdot \frac {15 \text{min}}{60 \text{min}}=12 \text{km/t} \cdot \frac 12 \text{t}+ 18 \text{km/t} \cdot \frac 14 \text{t} =6 km + 4,5 km = 10,5 km\approx 11 km</tex>

c)

Funksjonsuttrykket for de første 30 minuttene er:

<tex>y=\frac {12}{60}x= \frac 15 x=0,20x</tex> gjelder når <tex>x \in \left[0,30\right] </tex> (sagt med ord: når <tex>x</tex> er fra og med 0 til og med 30).

Funksjonsuttrykket for de neste 30 minuttene er:

<tex>y=\frac {18}{60}x= \frac 3{10} x=0,30x</tex> gjelder når <tex>x \in \left\langle30,60\right] </tex>(sagt med ord: når <tex>x</tex> er fra 30 til og med 60).

Oppgave 5

a)

Lager krysstabell, setter inn verdiene fra oppgaven og regner ut de andre slik at tabellen blir fullstendig:

	Briller B	Ikke briller <tex>\bar{B}</tex>	Sum
Kontaktlinser L	<tex>9,7 \percent</tex>	<tex>7,2 \percent</tex>	<tex>9,7 \percent +7,2 \percent=16,9 \percent</tex>
Ikke kontaktlinser <tex>\bar{L}</tex>	<tex>14,3 \percent</tex>	<tex>100 \percent - (14,3 \percent +7,2 \percent+ 9,7 \percent)=68,8 \percent</tex>	<tex>100 \percent -16,9 \percent =83,1 \percent</tex>
Sum	<tex>24,0 \percent</tex>	<tex>100\percent -24,0 \percent =76,0 \percent</tex>	<tex>100 \percent</tex>

b)

Som vi regnet ut i tabellen i a) er sannsynligheten for at en person ikke bruker briller <tex>76,0 \percent</tex>.

c)

Sannsynligheten for at en person som bruker briller også bruker kontaktlinser er:

<tex>\frac{9,7\percent \cdot 100}{24 \percent}=40,4 \percent</tex>

Oppgave 6

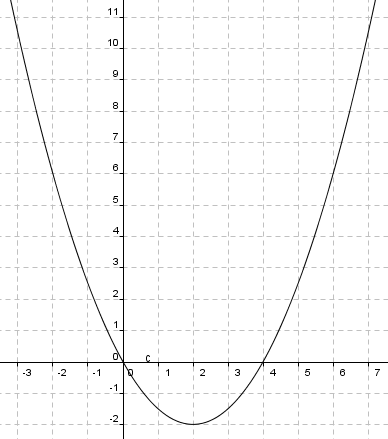
a)

b)

Grafen har nullpunkt når <tex>f(x)=0,5x^2-2x=0</tex>. Løser likningen <tex>0,5x^2-2x=0</tex> for å finne nullpunktene:

<tex>0,5x^2-2x=0 \Leftrightarrow x(0,5x-2)=0. \ \text{Produktsetningen gir da at x=0 eller 0,5x-2=0. Det vil si at } x=0 \ eller \ 0,5x-2=0 \Leftrightarrow 0,5x=2 \Leftrightarrow x=4</tex>.

Altså er <tex>f(x)=0</tex> når <tex>x=0</tex> og <tex>x=4</tex>. Dette kan kontrolleres ved å finne verdien av f(x) når x=0, og når x=4 ved å sette inn henholdsvis 0 og 4 for x i likningen:

<tex>f(0)=0,5 \cdot 0^2 -2\cdot 0=0</tex>

<tex>f(4)=0,5\cdot 4^2 - 2\cdot 4=0,5\cdot 16 -8=8-8=0</tex>

Det stemmer, altså er nullpunktene til funksjonen(på formen <tex>(f(x),x)</tex>): (0,0) og (4,0).

Oppgave 7

Alternativ I

a)

<tex>\left[{ 2y-x^2+2x=a \\ y-2x=3 }\right]</tex>

1)

Når a=6, er likningssettet: <tex>\left[{ 2y-x^2+2x=6 \\ y-2x=3 }\right]</tex>. Dette kan f.eks løses ved å

<tex>\left[{ 2y-x^2+2x=6 \\ y-2x=3 |\cdot -2}\right] \Leftrightarrow \left[{ (2y-x^2+2x=6) \\ \\+ \\ \\ (-2y+4x=-6)}\right] \Leftrightarrow 2y-2y-x^2+2x+4x=6-6 \Leftrightarrow -x^2+6x=0 x(6-x)=0 \Leftrightarrow x=0 \ eller \ x=6</tex>

Hvis x=0, er <tex>y=2x+3=2\cdot 0+3=3</tex> eller hvis x=6, er <tex>y=2x+3=2\cdot 6+3=15</tex>.

2)

b)

Setter inn x=1 og y=5 i den øverste likningen i likningssettet og løser for a:

<tex>a=2y-x^2+2x=2\cdot 5-1^2+2\cdot 1=10-1+2=11</tex>. Altså må a være lik 11 for at x=1 og y=5 skal være en løsning til likningen.

Alternativ II

a)

Vi deler opp arealet i to. Huset består av et kvadrat med areal <tex>a \cdot a =a^2</tex>

og et rektangel med areal <tex>3a(10-a) = 30a-3a^2</tex>

Det totale arealet blir da: <tex>a^2 +(30a-3a^2) = 30a-2a^2 </tex>

<tex>a=5 \Rightarrow 30 \cdot 5 - 2 \cdot 5^2 = 100</tex> kvadratmeter

b)

<tex>F(a) = 30a- 2a^2 \\ F(a) = 112 \\ -2a^2+30a -112 = 0 \\a=7 \vee a=8</tex>

c)

<tex>F(a) = 30a- 2a^2 \\ F'(a) = 30-4a \\F'(a) = 0 \\ 30-4a=0 \\ a=7,5 \\ F(7,5)= 112,5</tex>

Når a = 7,5m er huset 112,5 kvadratmeter

d)

<tex>-2a^2+30a =72 \\ a=3 \vee a=12</tex>

Huset er større enn 72 kvadrat meter når a er større enn 3m og mindre enn 12m