Sannsynlighet og kombinatorikk
Innledning
Sannsynlighet er et ”nytt” fagområder i matematikk. Grunnlaget ble lagt av Fermat og Pascal i 1654 og utviklingen har fortsatt til langt ut på 1900 tallet. Sannsynlighet brukes i dag blant annet innen spillteori, forsikring og økonomi, medisin, moderne fysikk, for å nevne noen områder.
Deterministisk eller tilfeldig
Hendelser som kan forutsies kalles deterministiske. Hendelser vi ikke kan forutsi, som for eksempel utfallet av et terningkast, kalles tilfeldige forsøk.
Vi skal her befatte oss med hendelser vi ikke kan forutsi, men som vi allikevel prøver å si noe om. På engelsk heter sannsynlighet probability. Derfor bruker man bokstaven P som symbolet for sannsynlighet.
”Sannsynligheten for regn i morgen” skrives P(regn i morgen).
”Sannsynligheten for å få terningkast seks” skrives P(6). Man kan også definer hendelsen for å få seks som A. Sannsynligheten for å få 6 øyner skrives da som P(A).
Utfallsrom
Hvor mange utfall kan et terningkast ha? En terning har seks flater med øyner fra en til seks, det betyr at utfallet vil være blant disse. Vi kaller alle mulige utfall for utfallsrommet. Et enkelt utfall vil være et element i utfallsrommet:
U = { 1, 2, 3, 4, 5, 6 }
Ufallsrommet ved et myntkast vil være: U = {kron, mynt}
Eksperimentell sannsynlighet - relativ frekvens - hyppighet
Hva er sjansen for å få fire øyner? Vi kan finne det ut på to måter, ved å gjennomføre mange terningkast, eller ved regning.
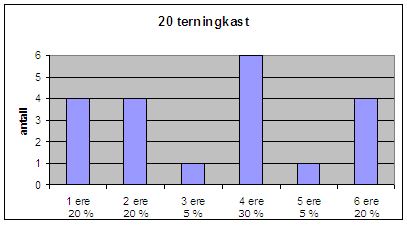
Vi lar datamaskinen kaste terning for oss, det kalles å simulere terningkast. På 20 kast får maskinen 6 firere. Den relative frekvensen for firere etter 20 kast er 6/20 = 0,3 eller 30%. Figur 1. viser fordelingen av øyner.
Figur 1.: Figuren viser fordelingen av øyner etter 20 terningkast.
Ut fra erfaring vil man kanskje forvente at sannsynligheten for å få firere skulle være den samme som å få treere eller femmere eller noe annet i utfallsrommet. Etter 20 terningkast kan man ikke trekke en slik konklusjon.
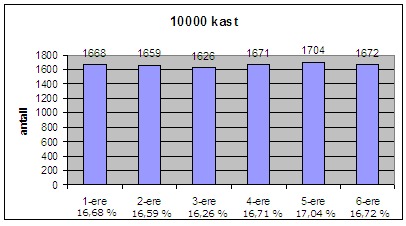
Vi setter maskinen til å kaste en terning 10.000 ganger. Det gir følgende resultat:
Figur 2.: Figuren viser fordelingen av øyner etter 10000 terningkast.
Nå ser det ut til at sannsynligheten for fire øyner går mot et tall som ligger rundt 0,16 – 0,17, dvs. 16 – 17%. Man ser at sannsynligheten for å få et annet antall øyner er nesten den samme.
Nå er ikke 10.000 det samme som "det lange løp", men tilstrekkelig til å se en tendens som bekreftes når vi behandler problemet teoretisk.
Teoretisk sannsynlighet
Utfallsrommet viser oss at det er seks mulige utfall når vi kaster en terning. Vi er bare interessert i å få en firer. Bare en av seks muligheter gir en firer. Det betyr at sannsynligheten for å få en firer i et kast er 1/6 eller 0,167 eller 16,7%. Vi kan skrive det slik:
P (4) = $\frac 16$ = 0,167 = 16,7%
Sannsynligheten kan altså presenteres som
Brøk
Desimalbrøk
Prosent
Presentasjonsformene er likeverdige men det er en god vane å holde seg til den formen som er gitt i oppgaven, dersom noe annet ikke er spesifisert.
Man forutsetter at sannsynligheten for å få et av de seks utfallene er den samme for alle utfall. Når det er slik sier vi at vi har en uniform sannsynlighet.
En sannsynlighetsmodell for et tilfeldig forsøk gir sannsynligheten for hvert enkelt utfall i utfallsrommet. Sannsynligheten for alle utfall i utfallsrommet er til sammen 1. Sannsynligheten for hvert enkelt utfall er mellom 0 og 1. Om våre teoretiske sannsynlighetsmodeller er gode, er det kun utprøving som kan fortelle oss.
Uniform sannsynlighet
Når sannsynligheten er den samme for alle elementer i utfallsrommet sier man at sannsynligheten er uniform – uniform sannsynlighet.
Når vi har en uniform sannsynlighetsmodell er sannsynligheten for en hendelse A gitt ved:
$$ P(A) = \frac{ \text{Antall gunstigen hendelser}}{\text{Antall mulige hendelser}} $$
Hva er sannsynligheten for å få en femmer eller en sekser i et terningkast? Sannsynligheten for å få en femmer er $\frac{1}{6}$ og sannsynligheten for å få en sekser er $\frac{1}{6}$. Sannsynligheten for femmer eller sekser blir da:
P(5 eller 6) = P(5) + P(6) = $ \frac{1}{6} + \frac {1}{6} = \frac {1}{3} $
Grafiske presentasjoner
Venndiagram
Et venndiagram er en grafisk fremstilling av en eller flere mengder, og eventuelle delmengder. Størrelsen av arealet i diagrammet har ingen matematisk betydning.
Eksempel:
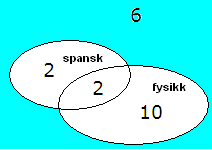
I en klasse på 20 elever har 4 elever spansk og 12 elever fysikk. 2 elever har begge deler. Denne situasjonen kan fremstilles i et Venndiagram:
Et venndiagram kan skape klarhet i situasjonen: 6 elever (blå) har ikke spansk eller fysikk. 2 elever har både fysikk og spansk. 4 (2+2) elever har spansk og 12 elever har fysikk. 10 av disse har ikke spansk. Det totale antall elever er 20. En feil som ofte gjøres er at de elementer som er med i flere mengder (spansk og fysikk) telles to (eller flere) ganger.
Krysstabell
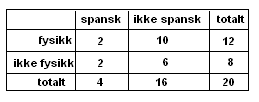
Situasjonen med elever i spansk og fysikk kan også presenteres i form av en krysstabell. Da ser det slik ut:
Poenget med begge presentasjonsformer (og med valgtre som kommer lenger nede på siden) er å systematisere ved utvelgelse, slik at det blir lettere å se hva som er gunstig av antall mulige.
Valgtre
Som du ser er presentasjonsmåtene forskjellige og har sine styrker og svakheter. Venndiagram brukes når du ønsker å vise forholdet mellom ulike grupper (mengder) og deres overlapping. Det brukes for å identifisere hva som er felles mellom grupper og hva som er unikt. Det gir en rask visuell forståelse av forholdet mellom grupper og er effektivt for små mengder kategoriske data. Krysstabeller brukes for å vise sammenhenger mellom to eller flere kategoriske variabler. De er spesielt nyttige for å finne korrelasjoner og sammenligne frekvensfordeling. De gir detaljert oversikt over data, egnet for kvantitativ analyse og det er lett å beregne sannsynligheter og avhengigheter (f.eks. chi-kvadrat-test). Valgtre brukes når man vil vise hendelser som skjer i rekkefølge, særlig når hver hendelse påvirker sannsynligheten for den neste. Det er egnet for å kartlegge mulige utfall og deres konsekvenser.
Komplementære hendelser
I en klasse har noen elever spansk valgfag. Man skal velge ut en elev fra klassen, og definere hendelse A = ”elev har spansk valgfag”. Alle elever som ikke har spansk valgfag vil inngå i mengden som er komplementær til A.
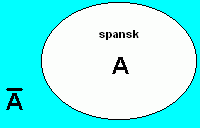
"ikke A" skrives slik: $\bar{A}$
Situasjonen kan se slik ut presentert i et Venndiagram:
I figuren over er $\bar{A} $ antall elever som IKKE har spansk.
Vi har at
$$P(A)+P(\bar{A})=1$$
Eks
På en skole er sannsynligheten for at en elev har spansk 0,23. . Hva er sannsynligheten for å trekke ut en tilfelidig elev, som ikke har valgt spansk?
$P(\overline{spansk}) = 1-0,23 = 0,77$
Union og snitt
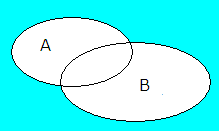
Union og snitt er begreper som kommer fra mengdelæren. Eksempelvis er A alle som liker matematikk og B er de som liker softis.
Union
Union mellom A og B er da som liker is ELLER de som liker matematikk ELLER de som liker begge deler. Union symboliseres med U.
De som liker matematikk eller softis eller begge deler befinner seg i venndiagrammets hvite del, <math>A\cup B </math>.
Sannsynligheten for å trekke en person som liker softis eller matematikk, eller begge deler blir
<math>P(A\cup B) </math>
Snitt
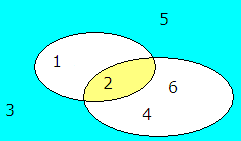
A snitt B er de som liker matematikk OG softis. Symbolet er ∩ og det kan se slik ut i et Venndiagram:
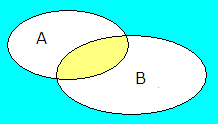
De som liker både matematikk og softis befinner seg i venndiagrammets gule del,
<math>A\cap B </math>.
Sannsynligheten for å trekke en person som liker softis og matematikk blir
<math>P(A\cap B) </math>
Disjunkte hendelser
A og B er disjunkte mengder fordi ingen elementer er felles. Dersom A er personer som liker is og B er personer som liker brus er det i denne mengden ingen personer som liker både brus og is. Det er imidlertid en gruppe (blått) som liker verken is eller brus.
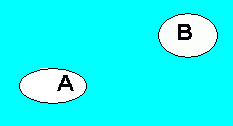
Siden A og B ikke har noen felles elementer skriver vi A ∩ B = Ø. Tegnet Ø betyr den tomme mengde.
Addisjonssetningen
Den generelle addisjonssetningen er gitt som:
$$P(A\cup B) = P(A) + P(B) - P(A\cap B) $$
Eksempel
Vi kaster en terning en gang. Hendelsen øyner mindre eller lik to kaller vi A, A={1,2}. Hendelsen partall kaller vi B, B = {2,4,6}
I et venndiagram ser det slik ut:
Sannsynligheten for A blir P(A) = $ \frac 26 = \frac 13$
Sannsynligheten for B blir P (B) = $\frac 36 = \frac 12$
Hva er sannsynligheten for A U B?
Vi bruker addisjonssetningen og får: P(AUB) = P(A) + P(B) - P(A ∩ B) = $ \frac 13 + \frac 12 - \frac 16 = \frac{2+3-1}{6} = \frac 23 $
Sannsynligheten for A ∩ B blir:
$P(A ∩ B) = P(A) + P(B) - P(A \cup B)= \frac 13 + \frac 12 - \frac 23 = \frac 16 $
Man ser, både av venndiagrammet og av addisjonssetningen hvorfor man må trekke fra
P(A ∩ B). Dersom vi ikke hadde gjort det hadde vi regnet med elementet 2 en gang for mye.
Addisjonssetningen for disjunkte hendelser
Disjunkte hendelser mangler noen felles elementer. Derfor blir addisjonssetningen for disjunkte hendelser:
$$P(A\cup B) = P(A) + P(B) $$
Betinget sannsynlighet
Med betinget sannsynlighet menes sannsynligheten for en hendelse når man har opplysninger om at en annen hendelse allerede har inntruffet.
Sannsynligheten for hendelse A gitt at hendelse B har inntruffet skrives:
P(A|B)
Man leser: "sannsynlighet for a gitt b". Vi har P(A∩B) = P(B) ∙ P(A|B)
Produktsetningen
Dersom hendelsene A og B skal inntreffe må først A inntreffe så må B inntreffe. Dersom sannsynligligheten for B er avhengig av om A inntreffer eller ikke, blir sannsynligheten for at A og B inntreffer:
$$P(A \cap B) = P(A)\cdot P(B|A) $$
Uavhengige hendelser
To hendelser A og B er uavhengige dersom
P(A) = P(A|B), som fører til uavhengighetskriteriet:
P(A∩B) = P(A) ∙ P(B)
Uavhengige hendelser forveksles av og til med disjunkte hendelser. For disjunkte hendelser gjelder
P(A∩B) = 0
Produktsetningen for uavhengige hendelser
Dersom man kaster en terning to ganger vil ikke resultatet fra første kast påvirke resultatet i andre kast. Hendelsene er uavhengige. Produktsetningen for uavhengige hendelser er:
$$P(A \cap B) = P(A)\cdot P(B) $$
Eksempel:
Hva er sannsynligheten for å få tre øyner i første kast og seks øyner i andre kast, når en terning kastes to ganger?
Sannsynligheten blir $P( 3 \cap 6) = \frac 16 \cdot \frac 16 = \frac{1}{36}$
Valgtre
Vi skal se litt nærmere på valgtre, som kan være en god grafisk presentasjon når betinget sannsynlighet er involvert.
Eks:
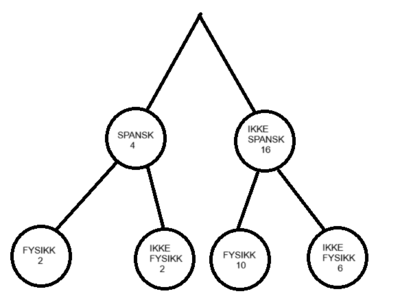
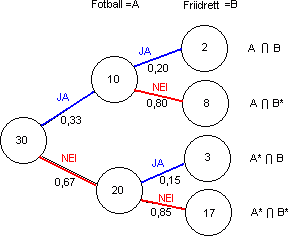
I en gruppe på 30 spiller 10 personer fotball (A). I den samme gruppen driver 5 personer friidrett (B). To personer bedriver begge deler. Det leder til følgende valgtre:
Vi finner følgende sannsynligheter:
Sannsynligheten for at en tilfeldig elev ikke spiller fotball:
<math> P( \bar A) = \frac{20}{30}= 0,66</math>
Sannsynligheten for at en tilfeldig elev spiller fotball:
<math> P(A) = \frac{10}{30}= 0,33</math>
eller slik:
<math> P(A) = 1 - P( \bar A)= 1 - \frac{20}{30}= 0,33</math>
Sannsynligheten for at en tilfeldig elev spiller fotball og driver friidrett:
<math> P(A \cap B) = P(A) \cdot P(B|A)= 0,33 \cdot 0,2 = 0,07</math>
Sannsynligheten for at en tilfeldig elev spiller fotball, men ikke driver friidrett:
<math> P(A \cap \bar B) = P(A) \cdot P( \bar B|A)= 0,33 \cdot 0,8 = 0,27</math>
Sannsynligheten for at en tilfeldig elev ikke spiller fotball, men driver friidrett:
<math> P(\bar A \cap B) = P(\bar A) \cdot P( B| \bar A)= 0,67 \cdot 0,15 = 0,10</math>
Sannsynligheten for at en tilfeldig elev ikke driver med fotball eller friidrett:
<math> P(\bar A \cap \bar B) = P(\bar A) \cdot P( \bar B| \bar A)= 0,67 \cdot 0,85 = 0,57</math>
Man observer at summen av sannsynlighetene på hver enkelt gren av treet blir lik 1.
Tilnærmingen skyldes avrundingen i mellomregningen
Total sannsynlighet
Treet over gir oss sannsynligheten for å velge ut en fotballspiller direkte. Dersom man ønsker å finne sannsynligheten for å trekke ut en friidrettsutøver, uavhengig av fotball, er ikke det fullt så åpenbart.
Sannsynligheten for å velge en person som driver friidrett er på grenene "fotball og friidrett" og "ikke fotball og friidrett". Litt mer matematisk blir sannsynligheten slik:
<math>P(B) = P(A \cap B)+ P(\bar A \cap B) = 0,07 + 0,10 = 0,17 </math>
Dette kalles gjerne den totale sannsynlighet (for B).
Bayes formel
Friidrett = B og fotball = A En elev driver friidrett. Hva er sannsynligheten for at eleven også spiller fotball? Vi ønsker å finne P(A | B). Vi har:
P( fotball og friidrett ) = P (friidrett) · P ( fotball gitt friidrett )
Litt mer matematisk:
<math>P(A \cap B) = P(B) \cdot P(A|B) </math>
er også det samme som
<math>P(B \cap A) = P(A) \cdot P(B|A) </math>
Setter man de to uttrykkene lik hverandre får man
<math>P(A) \cdot P(B|A) = P(B) \cdot P(A|B) </math>
som gir:
<math> P(B|A) = \frac{P(B) \cdot P(A|B)}{P(A)} </math>
Man har nå en sammenheng mellom en betinget sannsynlighet og den motsatte betingede sannsynligheten. Relasjonen eller formelen kalles for Bayes setning.
Eks:
tidligere 2MX eksamensoppgave
Livmorkreft er en kreftform som kan ramme voksne kvinner i alle aldere. Celleforandringer i livmorhalsen kan være forstadier til kreft. De kan påvises ved celleprøver. Kreftregisteret anbefaler alle kvinner mellom 25 og 69 år å ta en slik celleprøve hvert tredje år. Resultatene av slike celleprøver er likevel ikke helt sikre. Fra medisinske undersøkelser har en erfart at
-For en kvinne som har celleforandringer i livmorhalsen, vil en celleprøve avsløre det i 75% av tilfellene.
-For kvinner som ikke har celleforandringer i livmorhalsen, vil en celleprøve likevel tyde på celleforandringer i 5% av tilfellene.
Vi går ut fra at 3% av de kvinner som tar celleprøver, faktisk har celleforandringer i livmorhalsen. Vi tar for oss en kvinne som tar celleprøven og innfører hendingene:
C: " Kvinnen har celleforandringer i livmorhalsen."
T: "Celleprøven tyder på at kvinnen har celleforandringer i livmorhalsen."
Opplysningene over gir disse sannsynlighetene
P(C) = 0,03
P(T|C) = 0,75
<math>P(T \cap \bar C) = 0,05 </math>
a) Finn <math>P(C \cap T) </math> og <math>P(\bar C \cap T) </math>
<math>P(C \cap T) </math>er sannsynligheten for "celleforandring" OG "prøven tyder på celleforandring". Vi får
<math>P(C \cap T)= P(C) \cdot P(T|C)= 0,03 \cdot 0,75 = 0,0225</math>
eller 2,25%
<math>P(\bar C \cap T) </math> er sannsynligheten for "ikke celleforandring " OG "prøven tyder på celleforandring". Vi
får :
<math>P(\bar C \cap T) = P( \bar C ) \cdot P(T| \bar C) = 0,97 \cdot 0,05 = 0,0485</math>
eller 4,85%
b) Vis at P(T) = 0,071
T er hendelsen at prøven tyder på celleforandring. Man må huske på at hendelsen kan inntreffe både ved "celleforandring" og "ikke celleforandring". Man finner den totale sannsynlighet for T slik:
$P(T)= P( \bar C \cap T) + P(C \cap T) = P( \bar C) \cdot P(T| \bar C) + P(C) \cdot P(C|T)$
$ = 0,0225 + 0,0485 = 0,071$
c) Gå ut fra at en celleprøve tyder på at en kvinne har celleforandringer i livmorhalsen. Hva er da sannsynligheten for at det virkelig er tilfelle?
Her spørres det om sannsynligheten for celleendringer når testen indikerer dette, Altså P(C|T). Man observerer at dette er den omvendte betingede sannsynligheten, i forhold til P(T|C) som allerede er kjent. Siden både P(C) og P(T) er kjent kan man anvende Bayes setning og får:
$P(C|T) = \frac{P(C) \cdot P(T|C)}{P(T)} = $
$\frac{0,03 \cdot 0,75 }{0,071} = 0,32$
eller 32%
Man observerer at selv om testen er positiv er det 32% sjanse for at kvinnen er frisk.
Dersom en celleprøve tyder på at en kvinne har celleforandringer i livmorhalsen, vil legen hennes følge opp med flere undersøkelser for å avgjøre om det virkelig er tilfellet. Selv om det viser seg at hun faktisk har celleforandringer, trenger det ikke være så alvorlig.
60% av slike celleforandringer går over av seg selv, mens resten kan behandles med et relativt enkelt inngrep.
Tenk deg at ti kvinner etter grundige undersøkelser har fått bekreftet at de har celleforandringer i livmorhalsen.
d) Hva er sannsynligheten for at celleforandringene går over av seg selv for minst åtte av kvinnene?
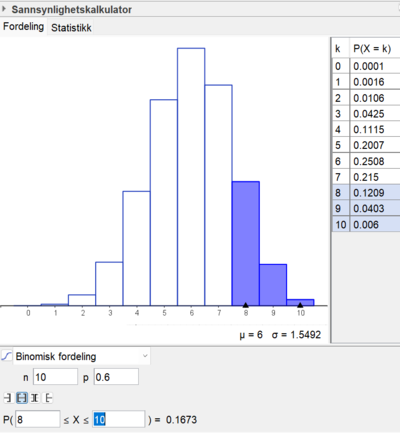
$ P(X=8)+ P(X=9) + P(X=10) = $
$\binom{10}{8} 0,6^8 \cdot 0,4^2 + \binom{10}{9} 0,6^9 \cdot 0,4^1 + \binom{10}{10} 0,6^{10} \cdot 0,4^0 = $
$
0,12 + 0,04 + 0,01 = 0,17 $
På Geogebra:
Kombinatorikk
Innledning
For å kunne beregne sannsynligheter trenger man en oversikt over mulige utfall og kombinasjoner. I den forbindelse kan det være greit med noen regler for å få klarhet når situasjoner virker uoversiktlige.
Multiplikasjonsregelen
Dersom situasjonen består av flere trinnvise valg mellom flere elementer blir antall kombinasjoner som følger.:
Antall elementer i første valgrunde multiplisert med antall elementer i andre runde osv.
m ∙ n ∙ …..
Eksempel:
Hvor mange antrekk kan du velge dersom du har valget mellom to gensere, fire bukser og tre par sko?
Svar:
2 (gensere) ∙ 4 (bukser) ∙ 3 (par sko) = 24 (antrekk)
Fakultet
På hvor mange måter kan 5 personer plassere seg i en 5 seters sofa? Første person kan velge mellom 5 seter, andre person mellom 4 osv. Det gir følgende antall kombinasjoner
5∙(5-1) ∙(5-2) ∙(5-3) ∙ (5-4) = 5!
n artikler kan arrangeres på :
n ∙(n-1) ∙(n-2) ∙………..1 = n!
n! leses ”n fakultet”.
0! defineres lik 1
10! = 10∙9∙8∙7∙6∙5∙4∙3∙2∙1= 3628800
Som man observerer blir fakulteter raskt store størrelse.
På hvor mange måter kan bokstavene a, b, c, d og e arrangeres?
Fem bokstaver kan arrangeres på 5! Måter, altså 5! = 120 måter.
Ordnet utvalg med tilbakelegging
Vi har 4 kuler i en urne. Kulene er nummererte fra 1 til 4. Dersom vi trekker en gang har vi fire muligheter. Når vi har trukket legger vi kulen tilbake igjen og trekker på nytt, slik at det blir 4 muligheter i andre trekning også.
Dersom man foretar r trekninger blant n elementer gir det
<math>n^r</math> muligheter. Rekkefølgen spiller en rolle slik at {1,2,3,3} er forskjellig fra {1,3,2,3}
<math>3^{12} = 531.441</math> måter.
Ordnet utvalg uten tilbakelegging
Dersom man har 10 kuler og skal trekke ut tre uten tilbakelegging vil man ha følgende muligheter:
1. trekning: 10 muligheter
2. trekning: 9 muligheter
3. trekning: 8 muligheter
Det gir oss 10 ∙ 9 ∙ 8 = 720 mulige kombinasjoner. Vi snakker om ordnede utvalg slik at {1,2,3} er forskjellig fra {1,3,2}, dvs. rekkefølgen spiller en rolle.
Dersom man trekker r elementer fra mengden n uten tilbakelegging skrives det nPr og kalkulatoren bør ha en funksjon for det. P står for permutasjoner. nPr er gitt som:
<math>nPr = n(n-1)(n-2).....(n-r+1) = \frac{n!}{(n-r)!}</math>
<math>500P4 = \frac{500!}{(500-4)!} = \frac{500!}{(496)!} =500 \cdot 499 \cdot 498 \cdot 497 = 6,18 \cdot 10^{10} </math> mulige permutasjoner.
Uordnet utvalg uten tilbakelegging
Dersom man skal velge ut to personer til en komité spiller det ingen rolle om man blir valgt som nummer en eller nummer to, enten er man med i komiteen eller så er man det ikke. Situasjonen kalles uordnet utvalg uten tilbakelegging. I slie situasjoner er {Eva, Ivar} identisk med {Ivar, Eva}. Om man tar utgangspunkt i formelen for ordnede utvalg og dividerer på antall muligheter de uttrukne elementene kan kombineres på får man:
<math>nCr = \frac{nPr}{r!} = \frac{n!}{r!(n-r)!} </math>
Som er formelen for uordnede utvalg uten tilbakelegging eller binominalkoeffisienten. Den skrives også Slik:
<math> nCr = {n \choose r} </math>
<math>500C4 = \frac{500P4}{4!} = \frac{500!}{4!496!}=2,57 \cdot 10^{9} </math>
Sannsynlighetsfordelinger
Her behandles binomisk fordeling og hypergeometrisk fordeling. Det finnes mange flere.
Binomisk fordeling
En binomisk sannsynlighetsmodell kan brukes dersom følgende tre kriterier er oppfylt:
- Et forsøk består i om en hendelse inntreffer eller ikke, altså kun to mulige utfall.
- Sannsynligheten p for at hendelsen skal inntreffe er den samme i alle forsøk
- Forsøkene er uavhengige av hverandre slik at resultatet fra et forsøk ikke virker inn på det neste.
Vi kaller dette en binomisk forsøksrekke. Dersom X er antall utfall i en binomisk forsøksrekke der hendelsen inntreffer er X en diskret stokastisk variabel med følgende sannsynlighetsfordeling:
<math> P(X=x)= \binom{n}{x} p^x \cdot (1-p)^{n-x}</math>
n er antall forsøk.
Forventningsverdien til X er:
E(X) = np
Variansen til X er:
Var (X) = np(1-p)
Eksempel 1:
Spireevnen til en type frø er 85%. Ti frø blir plantet. Hva er sannsynligheten for at 8 frø spirer?
<math> P(X=8)= \binom{10}{8} 0,85^8 \cdot 0,15^2 = 0,28</math>
Hypergeometrisk fordeling
Hypergeometrisk fordeling ligner på binomisk fordeling, men har følgende karakteristiske trekk:
- En populasjon med N elementer inneholder a elementer med en spesiell egenskap.
- Man foretar n trekninger UTEN tilbakelegging (sannsynligheten endrer seg).
- x er antall enheter med den bestemte egenskapen.
Sannsynligheten for at x av elementene som trekkes har egenskapen a er:
<math>P(X=x)=\frac{\binom{a}{x} \cdot \binom{N-a}{n-x} }{\binom{N}{n} }</math>
Eksempel 2:
En skuff består av 10 kniver med sort skaft og 5 kniver med rødt skaft. Man trekker 4 kniver uten tilbakelegging. Hva er sannsynligheten for at 3 av knivene som trekkes tilfeldig har rødt skaft?
<math>P(X=3)=\frac{\binom{5}{3} \cdot \binom{10}{1} }{\binom{15}{4} }= 0,073</math>
binomisk vs. hypergeometrisk fordeling
Den hypergeometriske fordelingen ligner på den binomiske, med den forskjell at sannsynligheten i delforsøkene IKKE er den samme.
Den hypergeometriske modellen brukes når populasjonen er liten og man trekker ut en betydelig del av den.
Dersom populasjonen er stor vil den hypergeometriske modellen nærme seg den binomiske og man bruker da den binomiske fordi den er lettest å arbeide med da den har færre parametere.
Dersom populasjonen er stor i forhold til utvalget (N > 10n) gjelder:
Hypergeometrisk fordeling (N,a,n) ≈ Binomisk fordeling (n,p)
<math>p = \frac aN</math>
Hvorfor er det slik?
Tenk deg en urne med et 50 kuler av to typer. Dersom du trekker ut 20 kuler uten tilbakelegging, altså en stor andel av det totale antall kuler i urnen, vil sannsynligheten endre seg betydelig for hvert trekk. Dette er en hypergeometrisk situasjon.
Eksempel 3:
I en urne finnes 40 kuler av type A og 10 kuler av type B. Man trekker ut 20 kuler uten tilbakelegging. Hva er sannsynligheten for å trekke 5 kuler av type B?
Ved å regne hypergeometrisk får man
<math>P(X=5)=\frac{\binom{10}{5} \cdot \binom{40}{15} }{\binom{50}{20} }= 0,22</math>
Dersom man regner binomisk får man
<math> P(X=5)= \binom{20}{5} 0,2^5 \cdot 0,8^{15} = 0,17</math>
Man observerer at det er stor forskjell på de to svarene, det første er riktig.
Dersom man har en urne med 1000 kuler og trekker ut 20 kuler uten tilbakelegging vil endringen i sannsynlighet være neglisjerbar. Dette er også en hypergeometrisk situasjon, men siden endringen i sannsynlighet er neglisjerbar kan man regne binomisk da det gir enklere regning.
Eksempel 4:
I en urne finnes 800 kuler av type A og 200 kuler av type B. Man trekker ut 20 kuler uten tilbakelegging. Hva er sannsynligheten for å trekke 5 kuler av type B?
Ved å regne hypergeometrisk får man
<math>P(X=5)=\frac{\binom{200}{5} \cdot \binom{800}{15} }{\binom{1000}{20} }= 0,176</math>
Dersom man regner binomisk får man
<math> P(X=5)= \binom{20}{5} 0,2^5 \cdot 0,8^{15} = 0,17</math>
Man observerer at fordelingene nærmer seg hverandre når populasjonen er stor i forhold til det antall man trekker ut.