R1 2024 Høst LØSNING
Diskusjon av oppgaven på matteprat
Løsningsforslag av Lektor Seland
DEL EN
Oppgave 1
Deriverer f:
Oppgave 2
Programmet leter etter toppunktet til funksjonen
Programmet løper gjennom en while løkke og sjekker funksjonsverdien O(x+1) i forhold til O(x). Så lenge O(x+1)> O(x) fortsetter løkken. Når det ikke lenger er tilfellet, skriver det ut x- verdien.
Vi deriver O og setter uttrykket lik null.
Programmet skriver ut 10000, som er x verdien som gir størst funksjonsverdi.
Oppgave 3
Vi er bare interessert i den positive verdien fordi vi ikke kan opphøye 10 i noe som gir en negativ verdi.
Oppgave 4
Oppgave 5
a)
Lengden av vektorene avgjøres av koordinatenes avstand fra origo. x og y koordinatene er katetene i en trekant der hypotenusen er selve vektoren. For lengden del er vi bare interessert i absoluttverdien og ser da at u og w vektor er like lange, altså
Ortogonale er et annet ord for vinkelrett på hverandre. Da er skalarproduktet lik null.
Disse to er det eneste som står vinkelrett på hverandre. Alle andre skalarprodukter her er forskjellig fra null, og da har man ikke ortogonalitet.
b)
Oppgave 6
Både g og f tilfredsstiller kravet om gjennomsnittlig vekstfart i intervallet [0,4]. g har derivert lik 0,5 for alle x, så det er kun f som tilfredsstiller kravene.
DEL TO
Oppgave 1
a)
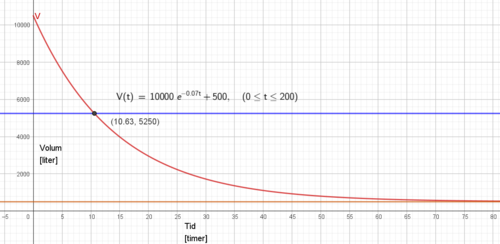
Vannmengden er halvert etter 10 timer og 38 minutter.
b)
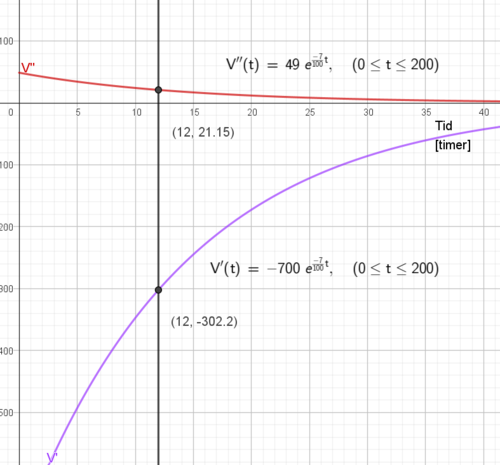
Den 12 timen reduseres vannmengden med ca 302 liter. Lekkasjen blir ca. 21 liter mindre i løpet av denne timen.
Vi ser at den deriverte av V er negativ. Det betyr at V minker. Den dobbeltderiverte av V, eller den deriverte av den deriverte, er positiv. Det betyr at den negative verdien til V derivert blir mindre negativ, altså at lekkasjen blir mindre.
c)
Fra figuren i a ser man at vannmengden nærmer seg 500 liter når tiden blir høy, så y = 500 er en horisontal asymptote.
En praktisk tolkning kan være at lekkasjen ikke er helt i bunnen, men et lite stykke oppe på reservoarveggen, slik at de 500 literne aldri renner ut.
Oppgave 2
a)
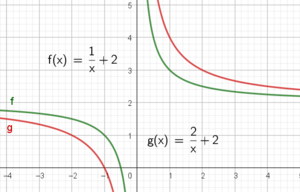
Begge går mot samme grenseverdi når x går mot pluss eller minus uendelig. Påstanden er feil.
b)
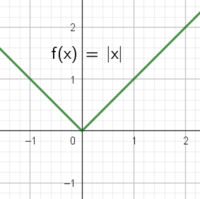
Det er riktig. Funksjonen er ikke deriverbar for X = 0.
Grafen har et knekkpunkt for x = 0 og er ikke deriverbar i dette punktet.
c)
Påstanden er feil for
a= - 1 gir løsninger når både x og y er partall, eller når begge er oddetall
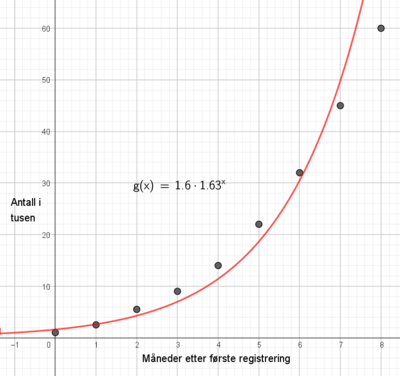
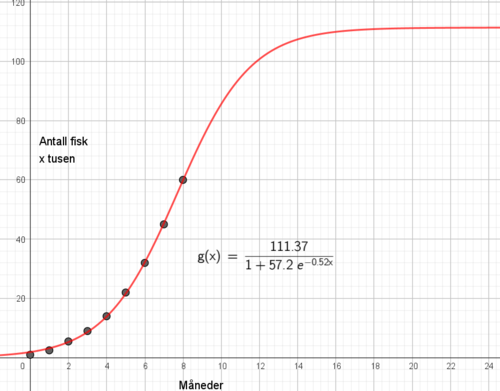
Oppgave 3
a)
b)
Bæreevne: B = 111 370 fisk
Vekstparameter: r = 0,52
For å finne hva modellen bruker som startverdi