2P 2024 Høst LØSNING
DEL EN
Oppgave 1
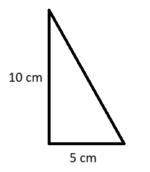
På et kart er avstanden mellom to byer 10 cm. I virkeligheten er denne avstanden 5 km.
Jeg gjør om 5 km til cm. 5 km = 5 000 m = 500 000 cm
10 cm på kartet = 500 000 cm i virkeligheten. Det vil si at 1 cm på kartet = 50 000 cm i virkeligheten.
Målestokken er 1 : 50 000
Oppgave 2
Her er antall timer Lars har arbeidet på butikken de siste 10 dagene:
3 3 4 5 6 8 0 3 5 5
a)
Gjennomsnitt:
$\frac{3+3+4+5+6+8+9+3+5+5}{10} = \frac{42}{10} = 4,2$
Lars har arbeidet i gjennomsnitt 4,2 timer per dag på butikken.
Sorterer tallene i stigende rekkefølge for å finne medianen:
0 3 3 3 4 5 5 5 6 8
Median:
$\frac{4+5}{2}= 4,5$
Medianen er 4,5 timer arbeid per dag.
b)
Jeg ser i tallrekka som er sortert i stigende rekkefølge at Lars arbeidet 5 timer eller mindre i 8 dager. Vi sier at den kumulative frekvensen for 5 timer er 8.
Oppgave 3
I en formlik trekant vil forholdet mellom sidene være det samme, så det lengste katetet skal være dobbelt så stort som det korterte katetet.
$\frac{grunnlinje\cdot høyde}{2}= Areal$
$\frac{x\cdot 2x}{2} = 64$
$x^2=64$
$x=\sqrt{64}$
$x=8$
Det korteste katetet skal være 8 cm og det lengste katetet skal være 16 cm i den nye trekanten.
Oppgave 4
I. $2x-6=y$
II. $4x+2y=12$
Bruker innsettingsmetoden, og setter inn uttrykket for y (gitt i likning I) inn i likning II.
$4x+2(2x-6)=12$
$4x+4x-12=12$
$8x=12+12$
$x={24}{8}$
$x=3$
Jeg setter inn verdien for x i likning I, for å finne verdien av y:
$2\cdot 3 - 6 = y$
$6-6=y$
$y=0$
Oppgave 5
a)
Uttrykket i linje 2 er en eksponentialfunksjon som uttrykket antall tonn CO2 bedriften slipper ut x år etter 2025.
200 er antall tonn CO2-utlipp i 2025.
0,975 er vekstfaktoren for en årlig nedgang i CO2-utslipp på 2,5 %.
b)
x er antall år, og s er summen av CO2-utslippene. Programmet regner ut summen av CO2-utslippene 4 år etter 2025 (altså i 2029).
DEL TO
Oppgave 1
$F(x)=620\cdot 1,045^x$
F viser hvor mange flasker iste en bedrift regner med å selge hver måned fra og med desember 2024.
a)
1)
Hvor mange flasker iste bedriften regner med å selge i desember 2025:
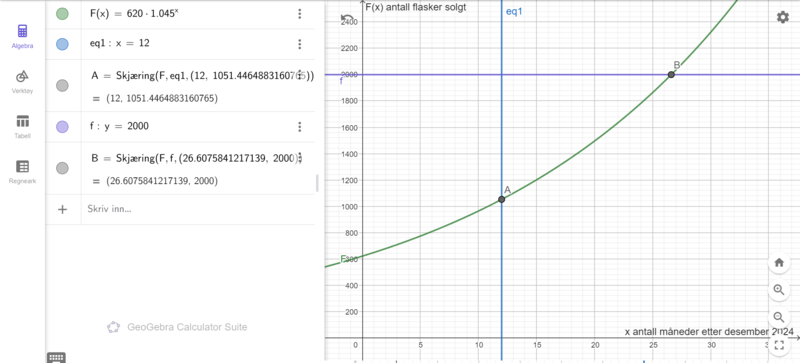
Metode 1, ved utregning: $F(12)=620 \cdot 1,045^{12}\approx 1051$
Metode 2, grafisk i Geogebra Suite:
Tegner grafen til F og linja x=12. Bruker deretter "skjæring mellom to objekt". Se punkt A.
Bedriften regner med å selge ca. 1051 flasker i desember 2025.
2)
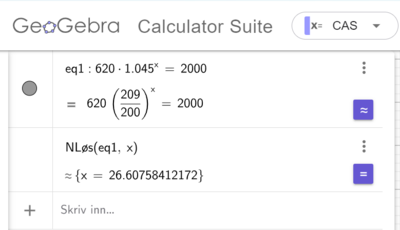
Når bedriften vil selge mer enn 2000 flasker i løpet av en måned:
Metode 1, ved utregning i CAS:
Metode 2, grafisk i Geogebra Suite (se skjermbilde i deloppgave 1):
Tegner grafen til F og linja y=2000. Bruker deretter "skjæring mellom to objekt". Se punkt B.
Bedriften regner med å selge 2000 flasker 26 måneder etter desember 2024, dvs i februar 2027.
b)
Jeg løser oppgaven på to måter.
1) Ved å bruke vekstfaktor:
$1,045^{24}=2,876$
En vekstfaktor på 2,876 betyr en økning i salget på 187,6 %.
2) Ved å bruke prosentregning:
Finner at $F(24)=1783$
Beregner prosent endring:
$\frac{1783-620}{620}\cdot100 \% = 187,6 \%$
Oppgave 2
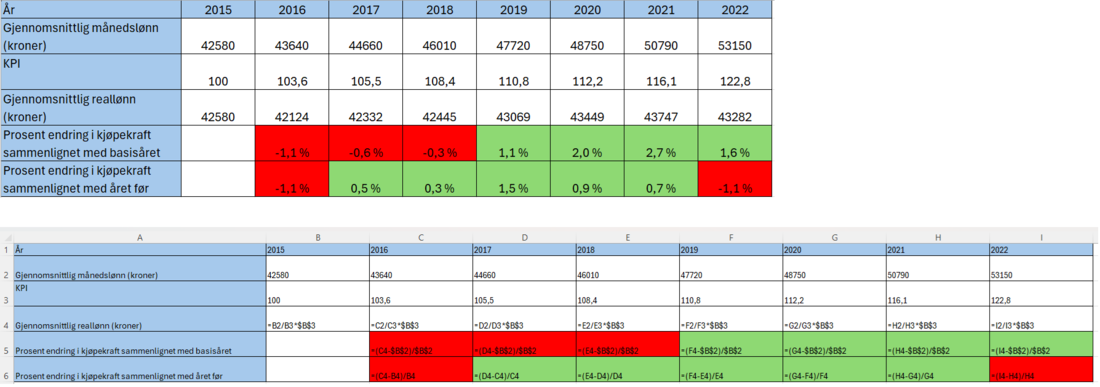
Jeg lager en oversikt i Excel. Jeg finner reallønna for hvert år, og finner deretter prosent endring i reallønn sammenlignet med basisåret, og sammenlignet med året før.
I 2017 og 2018 ser vi at kjøpekraften er dårligere enn den var i basisåret, men likevel bedre enn året før. I 2022 er kjøpekraften bedre enn i basisåret, men dårligere enn året før (2021).
Oppgave 3
For å finne 10 % av 50:
$x=\frac{10}{100}\cdot 50$
$x=\frac{10\cdot 50}{100}$
$x=5$
For å finne 50 % av 10:
$x=\frac{50}{100}\cdot 10$
$x=\frac{10\cdot 50}{100}$
$x=5$
Vi får alltid samme svar i slike tilfeller. Å finne p % av q eller q % av p er det samme.
$x=\frac{p}{100}\cdot q = \frac{q}{100}\cdot p = \frac{p\cdot q}{100}$
Oppgave 4
a)
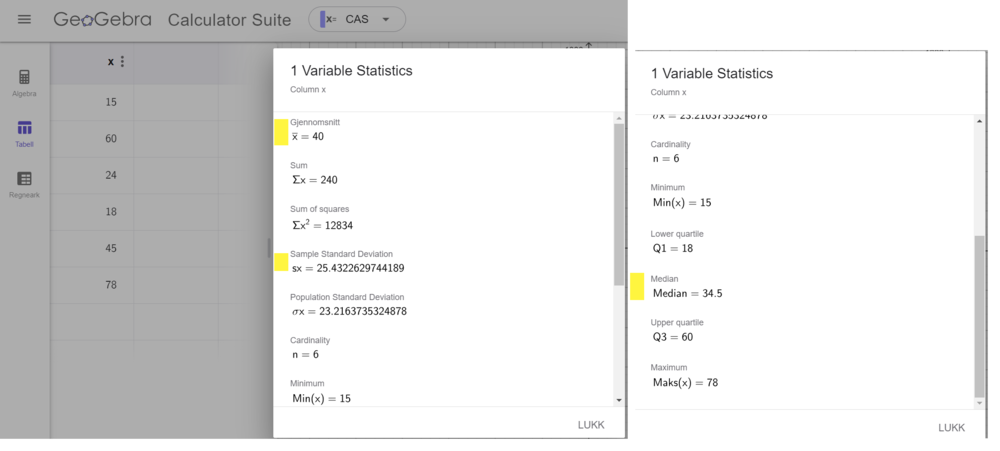
Jeg bruker Tabell i Geogebra Suite, legger inn tallene, og velger statistikk.
Gjennomsnittsalderen er 40 år, medianalderen er 34,5 år, og standardavviket er 25,4 år for lag A.
Jeg kunne også brukt Excel til denne oppgaven, se skjermbilde i oppgave c).
b)
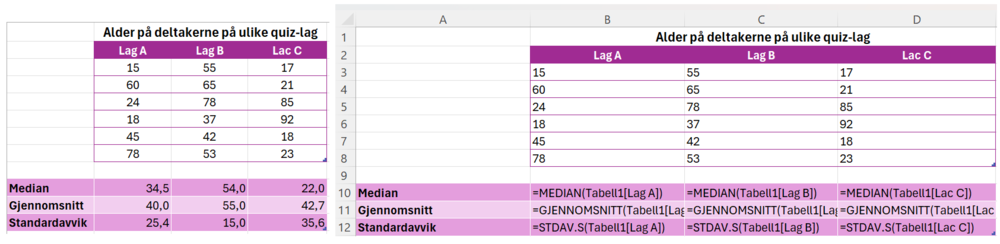
På lag B er både gjennomsnittsalderen og medianalderen høyere enn på lag A. Standardavviket er derimot lavere. Det vil si at deltakerne på laget jevnt over er eldre, og at det ikke er like stor aldersforskjell på dem.
På lag C er medianalderen lavere enn på lag A, men gjennomsnittsalderen og standardavviket er høyere. Det vil si at minst halvparten av deltakerne på lag C er yngre enn medianalderen på lag A. Men siden gjennomsnittsalderen er høyere enn på lag A, er det noen eldre deltakere som trekker gjennomsnittsalderen opp. Et større standardavvik betyr at aldersforskjellen er større blant deltakerne på lag C.
c)
Jeg bruker Excel til å sette opp et eksempel på aldersfordeling på lag B og C, og beregne median, gjennomsnitt og standardavvik for hvert av lagene, slik at det passer med opplysningene.
Oppgave 5
Bruker Excel til å bestemme nettolønna til Tobine. Nettolønna er 31 203,79 kr.