2P 2024 Høst LØSNING

DEL EN

Oppgave 1

På et kart er avstanden mellom to byer 10 cm. I virkeligheten er denne avstanden 5 km.

Jeg gjør om 5 km til cm. 5 km = 5 000 m = 500 000 cm

10 cm på kartet = 500 000 cm i virkeligheten. Det vil si at 1 cm på kartet = 50 000 cm i virkeligheten.

Målestokken er 1 : 50 000

Oppgave 2

Her er antall timer Lars har arbeidet på butikken de siste 10 dagene:

3 3 4 5 6 8 0 3 5 5

a)

Gjennomsnitt:

$\frac{3+3+4+5+6+8+9+3+5+5}{10} = \frac{42}{10} = 4,2$

Lars har arbeidet i gjennomsnitt 4,2 timer per dag på butikken.

Sorterer tallene i stigende rekkefølge for å finne medianen:

0 3 3 3 4 5 5 5 6 8

Median:

$\frac{4+5}{2}= 4,5$

Medianen er 4,5 timer arbeid per dag.

b)

Jeg ser i tallrekka som er sortert i stigende rekkefølge at Lars arbeidet 5 timer eller mindre i 8 dager. Vi sier at den kumulative frekvensen for 5 timer er 8.

Oppgave 3

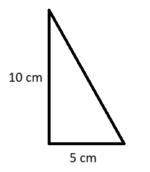
I en formlik trekant vil forholdet mellom sidene være det samme, så det lengste katetet skal være dobbelt så stort som det korterte katetet.

$\frac{grunnlinje\cdot høyde}{2}= Areal$

$\frac{x\cdot 2x}{2} = 64$

$x^2=64$

$x=\sqrt{64}$

$x=8$

Det korteste katetet skal være 8 cm og det lengste katetet skal være 16 cm i den nye trekanten.

Oppgave 4

I. $2x-6=y$

II. $4x+2y=12$

Bruker innsettingsmetoden, og setter inn uttrykket for y (gitt i likning I) inn i likning II.

II. $4x+2(2x-6)=12$

$4x+4x-12=12$

$8x=12+12$

$x={24}{8}$

$x=3$

Jeg setter inn verdien for x i likning I, for å finne verdien av y:

I. $2\cdot 3 - 6 = y$

$6-6=y$

$y=0$