Integrasjon

Innledning til integrasjon

Her prøver vi å gi en enkel framstilling av hva integraler kan være og hva integralregning kan brukes til.

Moped nr. 1

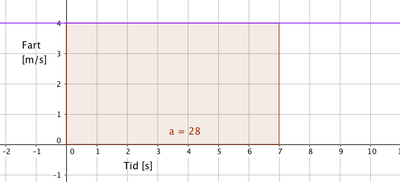
En moped beveger seg med konstant fart 4 meter per sekund. Grafisk kan det se slik ut:

Den fiolette linjen representerer grafen til funksjonen

f(t) = 4.

Vi er interessert i å se på arealet under grafen. Hva forteller det oss?

Mopeden kjører med konstant hastighet 4m/s i 7 sekunder.

I den perioden tilbakelegger den en strekning S på $S =v\cdot t = 4m/s \cdot 7s = 28m$.

Dersom vi teller antall ruter under grafen, eller regner ut arealet av rektangelet får vi også 28.

Arealet under grafen til funksjonen som utrykker hastighet som funksjon av tiden gir oss altså tilbakelagt strekning i samme tidsrom.

Legg merke til følgende:

Når vi skal tolke arealet under en graf er enheten for svaret alltid lik enheten på x- aksen multiplisert med enheten på y-aksen.

I eksemplet over gir det $s \cdot \frac ms = m$

Moped nr. 2

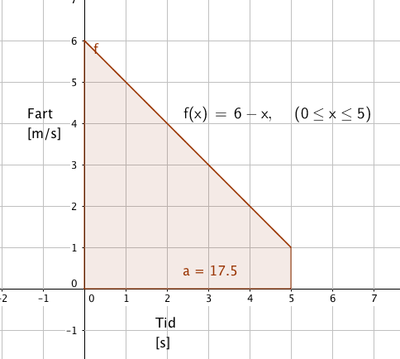
En annen moped kjører med hastigheten 6 meter per sekund og begynner så å bremse opp. Mopeden bremser med en jevn akselerasjon (negativ) fra 6m/s til 1 m/s. Funksjonen som beskriver situasjonen ser slik ut:

g(t) = 6 - t

Dette skjer i løpet av fem sekunder.

I dette eksemplet ser vi at arealet under grafen er 17,5 og at benevningen er m (meter), hvilket betyr at mopeden beveger seg 17,5 meter under oppbremsingen.

De to eksemplene over var med rette linjer, altså lineære funksjoner. Hva da når grafen krummer?

Når grafen krummer...

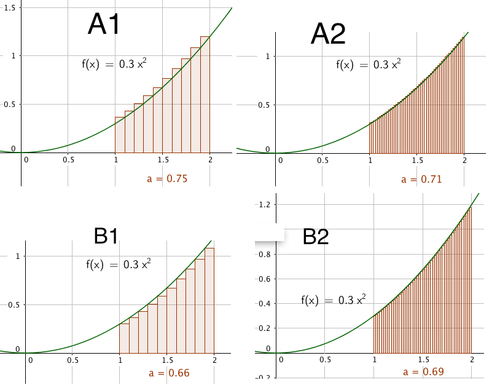
For å finne arealet under krumme kurver kan vi dele området opp i rektangler som vist under

Vi observerer følgende:

Rektanglene under kurven i figur A1 og A2 vil gi et større areal enn det som faktisk er under kurven.
Rektanglene under kurven i figur B1 og B2 vil gi et mindre areal enn det som faktisk er under kurven.
Bredden av rektanglene og derved også antall rektangler, har betydning for nøyaktigheten i resultatet. Både modell A og B vil bevege seg mot arealet under kurven, når antall rektangler går mot uendelig, og bredden av rektanglene avtar. Arealet under kurven er summen av disse rektanglene. Bredden av et rektangel er gitt ved:

$\Delta x = \frac{b-a}{n}$

Der n er antall rektangler, b er øvre grense og a er nedre grense som begrenser arealet under kurven.

Summen $S_n$ av rektanglene under grafen blir:

$S_n = f(x_1)\cdot \Delta x + f(x_2) \cdot \Delta x+..+f(x_n) \cdot \Delta x$ (kalles Riemannsum)

Det bestemte integralet til f er:

$\int\limits_a^b f(x)dx = \lim\limits_{n\to\infty}S_n$

Der f(x) er integranden, altså funksjonen som skal integreres. a er nedre integrasjonsgrense, b er øvre integrasjonsgrense. I vårt eksempel over er nedre grense en og øvre grense to. n er antallet rektangler. Vi observerte at når n går mot uendelig, går $\Delta x $ mot null og grensen går mot integralet. Når vi har integrasjonsgrenser som her kalles integralet for et bestemt integral. Et ubestemt integral er uten øvre og nedre grense.

Dersom det finnes en deriverbar funksjon F(x) er

F'(x) = f(x)

$\int f(x)dx = F(x) + C$

Der C er en konstant. Vi sier at F(x) er en antiderivert av f(x).

Det bestemte integralet blir da:

$\int\limits_a^b f(x)dx = F(b)- F(a)$

Der a og b er integrasjonsgrensene.

Du lurer kanskje på hva som skjedde med C? Dersom vi ser på høyre side av likhetstegnet ser vi at

F(b) + C - (F(a) + C) = F(b) - F(a)

Altså forsvinner C.

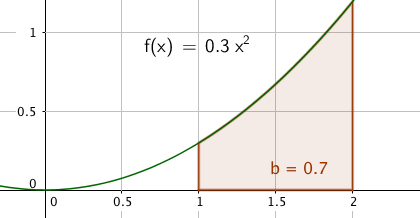
Det eksakte svaret på oppgaven er altså:

$\int\limits_1^2 0,3x^2 dx = [\frac{0,3}{3}x^3]_1^2 = 0,1(8-1)= 0,7$

Tilnærmingen med 50 rektangler (A2 og B2) var altså god.

Moped 1 og Moped 2 utsettes for integrasjon

La oss se på eksemplene i begynnelsen:

f(t) = 4 gir:

$\int\limits_0^7 4dt = [4t]_0^7 = 28 -0 = 28 $

Som var det samme resultatet vi fikk ved å telle ruter.

g(t) = 6 -t gir:

$\int\limits_0^5 (6-t)dt = [6t- \frac 12t^2]_0^5 = 30- 12,5 - 0 = 17,5$

Resultatet tilsvarer det vi fikk ved å telle ruter.

Er integral og areal det samme?

Så langt har vi sett på arealer avgrenset av x-aksen, a, b og en graf som ligger over x-aksen. Hva når grafen til funksjonen ligger under x-aksen?

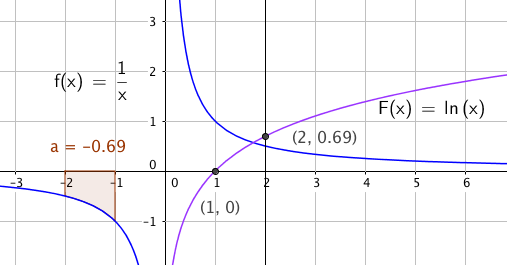
La oss finne det bestemte integralet avgrenset av x = -2, x = -1, x-aksen og funksjonen $f(x)= \frac 1x$

Geogebra gir oss et integral på - 0,69, Altså en negativ verdi. Regning for hånd gir:

$\int\limits_{-2}^{-1} \frac 1x dx dx = ln |-1| - ln |-2| = 0 - 0,69 = -0,69$

Man ser at dette stemmer med grafen til ln (x), som er tegnet lilla i samme koordinatsystem.

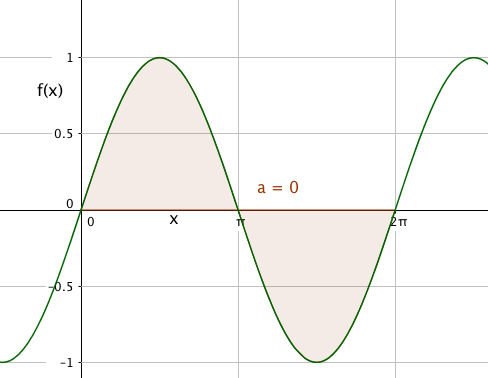
Et eksempel til:

f(x) = sin x

$\int\limits_0^{2\pi} (sinx) dx = [-cos x]_0^{2\pi} = -1 -(-1)= 0 $

Fra disse eksemplene ser vi at integralet og arealet IKKE er det samme, selv om vi kan tolke integralet geometrisk. Av og til ser man på integralet som et areal, andre ganger som en sum av ett eller annet.

Noen ganger kan det være vanskelig eller umulig å finne et utrykk for den antideriverte. Da kan man ta utgangspunkt i Riemannsummen og løse problemet numerisk.

Eller man kan gjøre som en professor jeg kjente. Han brukte saks, tykt papir og en nøyaktig vekt. Ved å klippe ut arealet under grafen og sammenligne det med et kjent areal, ved veiing, kom han fram til tilnærminger gode nok for de fleste ingeniørformål.

Integrasjon

Vi ser litt nærmere på integrasjon, teorien rundt og på en del integrasjonsformler.

Det bestemte integralet

Med det bestemte integalet av en funksjon vil vi finne arealet under funksjonen avgrenset av <math>x</math>-aksen og linjene <math>x=a</math> og <math>x=b</math>. "Det bestemte integralet av <math>f(x)</math> fra <math>a</math> til <math>b</math>" skriver vi som

Bestemt integral som grenseverdi

Vi kan se for oss arealet under en graf som en sum av rektangler, der antallet rektangler angir nøyaktigheten av integralet.

Dersom vi vil integrere <math>f(x)</math> fra <math>x=a</math> til <math>x=b</math> med <math>n</math> rektangler, må hvert rektangel ha bredde <math>\Delta x=\frac{b-a}{n}</math> (vi deler avstanden mellom endepunktene, <math>b-a</math> på antallet rektangler <math>n</math>.) Vi får da at

<math>A=\sum_{i=0}^n f(a+i\Delta x)\cdot \Delta x=\sum_{i=0}^n f\left( a+i\frac{b-a}{n}\right)\frac{b-a}{n}</math>

Når vi lar <math>\Delta x</math> gå mot null, dvs at vi lar antallet rektangler <math>n</math> gå mot uendelig, får vi det nøyaktige arealet under kurven:

<math>\int_a^b f(x)\rm{d}x=\lim_{n\to\infty} \sum_{i=0}^n f\left( a+i\frac{b-a}{n}\right)\frac{b-a}{n}</math>

Ubestemt integrasjon

I analysen (engelsk: Calculus) finnes et fundamentalteorem som relaterer operasjonene integrasjon og derivasjon med hverandre. Dette gjør det mulig å finne integralet av funksjoner uten å regne ut kompliserte summer som ovenfor. Teoremet er delt inn i to deler, som ofte kalles analysens første og andre fundamentalteorem.

Analysens første fundamentalteorem sier at hvis en reell funksjon <math>F(x)</math> er definert på intervallet <math>[a,b]</math> ved

der <math>f(t)</math> er en reell funksjon som er kontinuerlig på intervallet <math>[a,b]</math>, da er <math>F(x)</math> kontinuerlig på <math>[a,b]</math> og deriverbar på <math>(a,b)</math>, og man kan vise at <math>\frac{d}{dx}F(x)=f(x)</math>, og vi skriver at

Analysens andre fundamentalteorem sier at

<math>F(a)-F(b)</math> er lik arealet mellom <math>x</math>-aksen og funksjonen <math>f(x)</math> mellom <math>x=a</math> og <math>x=b</math>.

Her skal vi vise geometrisk at <math>\frac{d}{dx}F(x)=f(x)</math>:

Bevis: Den deriverte av den integrerte er funksjonen selv

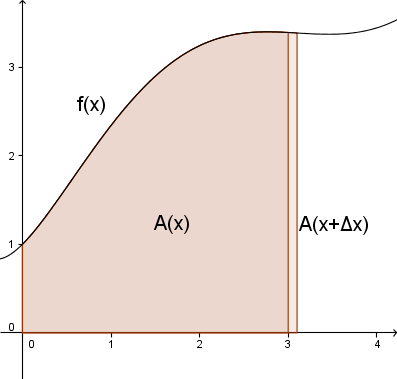
La <math>f(x)</math> være en reell funksjon <math>(f(x)\in\mathbb{R}</math>, for alle <math>x\in \mathbb{R})</math>, og la funksjonen <math>A(x)</math> beskrive arealet mellom <math>x</math>-aksen og <math>f(x)</math> ved at <math>A(b)-A(a)</math> er lik arealet mellom <math>x</math>-aksen og <math>f(x)</math> mellom <math>x=a</math> og <math>x=b</math>. Mellom <math>x</math> og <math>x+\Delta x</math> vil aralet altså være <math>A(x+\Delta x)-A(x)</math>, se figur:

I grenseverdien når <math>\Delta x\to 0</math> vil dette arealet bli tilnærmet et rektangel. Arealet av et rektangel er gitt ved

<math>A=l\cdot b</math>

og arealet at dette rektangelet ser vi ut ifra figuren blir <math>f(x)\cdot \Delta x</math>. Dermed kan vi konkludere at

<math>f(x)=\lim_{\Delta x\to0}\frac{A(x+\Delta x)-A(x)}{\Delta x}</math>

Men dette kjenner vi som definisjonen av den deriverte. Altså kan vi skrive at

<math>f(x)=\frac{d}{dx}A(x)</math>

Vi har dermed bevist at derivasjon og integrasjon er inverse operasjoner av hverandre, det vil si at

<math>\frac{d}{dx}\int f(x)\rm{d}x=f(x)</math>

Dette kan også vises analytisk ved å ta i bruk noe mer avansert funksjonslære.

Når vi antideriverer en funksjon, dvs at vi tar det ubestemte integralet av funksjonen, får vi altså funksjonen <math>F(x)</math> som inngår i fundamentalteoremet.

Formler for integrasjon

Her er noen nyttige formler for integrasjonen av sentrale funksjoner. Med metodene i de neste seksjonene vil vi også kunne integrere funksjoner sammensatt av disse. Denne tabellen må læres utenat.

$\int f(x) dx = F(x)$

f(x)	F(x)	Eksempel
$x^n$	$\frac{1}{n+1}x^{n+1} + C$	$f(x)=x^3$	$\int f(x) dx= \frac{1}{4}x^{4} + C$
$ \frac 1x$	ln x + C	x er positiv
$e^x$	$e^x +C $
$a^x$	$\frac{1}{ln a} a^x + C$
cos x	sin x + C
sin x	- cos x + C

Bestemte integgraler

$\int\limits_a^a f(x)dx =0$

$\int\limits_a^b kf(x)dx =k \int\limits_a^b f(x)dx $

$\int\limits_a^b f(x)dx = - \int\limits_b^a f(x)dx$

$ \int\limits_a^b f(x)dx + \int\limits_b^c f(x)dx = \int\limits_a^c f(x)dx$

$\int\limits_a^b (f(x)+g(x))dx= \int\limits_a^b f(x)dx + \int\limits_a^bg(x)dx$

Integrasjonskonstanten

Ettersom den deriverte av en konstant funksjon er lik null, må vi legge til en vilkårlig konstant til den integrerte av en funksjon.

Eksempel: Integrasjonskonstant

Vi tar for oss integralet

Vi vet at <math>\frac{d}{dx}\frac12x^2=x</math>, men siden <math>\frac{d}{dx}C=0</math>, der <math>C</math> er en konstant, må vi legge denne til. Svaret blir altså

Merk at integrasjonskonstanten blir kansellert når <math>F(x)</math> brukes i sammenheng med det bestemte integralet. Det viser at verdien til <math>C</math> er vilkårlig.

Integrasjonsmetoder

Variabelskifte

I derivasjon sier kjerneregelen at

Dermed følger det at

Når vi substituerer variabler i integranden, manipulerer vi også differensialene <math>\rm{d}x</math> og <math>\rm{d}u</math>. Derfor skal vi nå vise hvordan man finner relasjonen mellom disse differensialene for en generell substitusjon. Deretter kan denne metoden anvendes på forskjellige integraler når de ikke kan løses direkte.

Relasjoner mellom differensialer

En generell substitusjon er

Vi vil finne relasjonen mellom differensialene <math>\rm{d}x</math> og <math>\rm{d}u</math> slik at vi kan foreta et variabelskifte.

Dersom vi deriverer begge funksjonene mhp. x, får vi, ifølge kjerneregelen,

Vi ser dermed at relasjonen mellom differensialene er

eller

<math>f^\prime (x)\rm{d}x=g^\prime (u) \rm{d}u</math>

Nå som vi kan manipulere differensialene, viser vi et eksempel der vi får bruk for dette:

Eksempel 1: Variabelskifte

Vi har integralet

Vi observerer at <math>\frac{d}{dx}\ln\,x=\frac{1}{x}</math> og at begge disse er med i integranden. En god substitusjon her er derfor <math>\ln\,x=u</math>. Vi finner relasjonen mellom differensialene slik at vi kan gjennomføre variabelskiftet fra <math>x</math> til <math>u</math>.

<math>\frac{d}{dx}\ln\,x=\frac{du}{dx}\,\Leftrightarrow\,\frac{1}{x}\rm{d}x=\rm{d}u\,\Leftrightarrow\,\rm{d}x=x\rm{d}u</math>

Vi erstatter <math>\ln\,x</math> med <math>u</math> og <math>\rm{d}x</math> med <math>x\rm{d}u</math> i integranden. Da får vi

Vi substituerer tilbake fra <math>u</math> til <math>x</math> for å få svaret. <math>u=\ln\,x</math>, så

Eksempel 2: Variabelskifte

Vi har integralet

Vi vet at <math>\tan\,x=\frac{sin\,x}{\cos\,x}</math> og at <math>\frac{d}{dx}\sin\,x=\cos\,x</math>, si vi setter <math>u=\cos\,x</math>:

<math>u=\cos\,x\,\Rightarrow\,\rm{d}u=-\sin\,x\rm{d}x</math>

Vi setter inn i integralet og får

Vi kan nå erstatte u med x igjen får å få svaret vårt:

Eksempel 3: Variabelskifte

$ \int 4e^{2x+1}dx \qquad \qquad \qquad\qquad \qquad setter \qquad u = 2x + 1 $ $ \quad du = 2dx $

$\int 4e^{u}dx = \int 2e^{u}du = 2e^{u} + C = 2e^{2x+1} + C$

Eksempel 4: Variabelskifte

$ \int \frac{1}{1+ \sqrt{x}}dx $

$ u = 1 + \sqrt{x}$

$\frac{du}{dx}= \frac12x^{- \frac12}$

$du= \frac{1}{2 \sqrt{x}}dx$

$dx= 2 \sqrt{x}du $

$\int \frac{1}{u}dx = \int \frac{1}{u}2 \sqrt{x}du$

Man bruker at <math>u = 1 + \sqrt{x} </math> og får:

Substituerer tilbake til x og får:

Test deg selv

Grenser ved variabelskifte

Når vi bruker variabelskifte og vi har et bestemt integral, vil grensene for integralet endres slik at integralet ennå gjelder for samme intervall. Dette vises best gjennom et eksempel:

Eksempel: Endring av grenser ved variabelskifte

La oss si at vi har integralet

Vi ser at <math>\frac{d}{dx}\cos\,x=-\sin{x}</math> og velger substitusjonen <math>u=\cos\,x</math>. Da får vi

<math>\rm{d}u=-\sin\,x\rm{d}x\,\Rightarrow\,\frac{1}{-\sin\,x}\rm{du}</math>

Grensene på integralet må vi endre slik at vi ennå integrerer over samme intervall. Vi gjør dette ved å sette inn grensene for x og løse med hensyn på u. Den nedre grensen blir

<math>\cos\,0=u\,\Rightarrow\,u=1</math>

Den øvre grensen blir

<math>\cos\,\pi=u\,\Rightarrow\,u=-1</math>

Vi setter alt inn i integralet og får

<math>I=\int_1^{-1}u^2\frac{sin\,x}{-\sin\,x}\rm{u}\int_1^{-1}-u^2\rm{d}u=\left[-\frac13u^3\right]_1^{-1}=-\frac13(-1)^3-\left(-\frac13\cdot1^3\right)=2\cdot\frac13\cdot1^3=\frac23</math>

Delvis integrasjon

Vi kjenner allerede produktregelen fra dervasjon:

Delvis integrasjon er produktregelen på integralform. Her skal vi utlede formelen for delvis integrasjon fra produktregelen:

Utleding av delvis integrasjon fra produktregelen

Vi starter med produktregelen

<math>(uv)^\prime=u^\prime v+uv^\prime</math>

og trekker fra <math>u\prime v</math> på hver side av likhetstegnet:

<math>uv^\prime=(uv)^\prime-u^\prime v</math>

Så integrerer vi:

<math>\int uv^\prime \rm{d}x=\int (uv)^\prime-u^\prime v \rm{d}x=\int (uv)^\prime \rm{d}x-\int u^\prime v \rm{d}x=uv-\int u^\prime v \rm{d}x</math>

<math>\int uv^\prime \rm{d}x=uv-\int u^\prime v \rm{d}x</math>

Delvis integrasjon kan også skrives slik:

<math>\int u\rm{d}v=uv-\int v\rm{d}u</math>

ved at <math>\frac{dv}{dx}\rm{d}x=\rm{d}v</math> og <math>\frac{du}{dx}\rm{d}x=\rm{d}u</math>.

Dersom integralet består av forskjellige typer funksjoner (for eksempel en polynomfunksjon multiplisert med en trigonometrisk funksjon) kan delvis integrasjon være et godt førstevalg. Man bør velge u til en funksjon som blir "enklere" etter derivasjonen. Av og til må man utføre delvis integrasjon to ganger før man kommer til et resultat.

Eksempel 1: integralet av naturlig logaritme

Vi vil integrere funskjonen <math>f(x)=\ln\,x</math>. Til det kan vi bruke et lite triks og delvis integrasjon.

Vi skriver <math>\ln\,x=1\cdot\ln\,x</math> og lar <math>u=\ln\,x</math> og <math>v=x</math>. Da får vi

<math>\frac{du}{dx}=1</math> og <math>\frac{dv}{dx}=\frac1x</math>. Integralet blir

Resultatet er altså at

Svaret kan kontrolleres ved derivasjon.

Eksempel 2:

$\int(3x+2)sinx dx$

Setter u = 3x + 2 og v' = sin x

u' = 3 og v = - cos x

og får da:

$\int(3x+2)sinx dx = (3x+2)\cdot (-cosx) - \int 3 \cdot (-cosx)dx = -(3x+2)cosx + 3 \int cosx dx \\ =-(3x+2)cosx + 3sinx + C $

Eksempel 3:

Her kommer en litt spesiell variant.

$\int sin^2x dx = \int (sinx \cdot sinx) dx $

$ = sinx \cdot (-cosx) - \int cosx \cdot (-cosx)dx $

$ - sinx cosx + \int (1-sin^2x) dx \\ = - sinx cosx + x - \int sin^2x dx$

Da har man:

$\int sin^2x dx = - sinx cosx + x - \int sin^2x dx$

$2\int sin^2x dx = - sinx cosx + x $

$\int sin^2x dx = - \frac12 (sinx cosx - x) + C$

Eksempel 4:

Av og til må man integrere to ganger.

setter <math>x^2 = u</math> og <math>e^x = v'</math>

da bli <math>u' = 2x</math> og <math> v=e^x</math>

da får man:

Så integrerer man en gang til og får:

Delbrøkoppspalting

Dersom man har en brøkfunksjon med en nevner som har høyere grad enn en og kan faktoriseres kan delbrøkoppspalting være en metode som fører til et resultat. Man ønsker å skrive en brøk med høyere grad enn en i nevner som summen av brøker med førstegradsuttrykk i nevneren. Teknikken illustreres best med et eksempel.

Eksempel 1:

$\int \frac{2x+3}{x^2-4}dx = \int \frac{2x+3}{(x-2)(x+2)}dx =\int (\frac{A}{(x-2)}+ \frac{B}{(x+2)})dx$

Man må så bestemme A og B. Det gjøres ved å løse likningen:

2x+3 = (x + 2)A + (x - 2)B

Velger x slik at parentesen foran A blir null og får x=-2 som gir:

Velger så x slik at parentesen foran B blir null, x = 2:

Integralet blir da:

<math> \int \frac{2x+3}{x^2-4}dx = \int \frac{2x+3}{(x-2)(x+2)}dx =\int (\frac{7}{4(x-2)}+ \frac

{1}{4(x+2)})dx = \frac 74 ln|x-2| + \frac14 ln|x+2| + C </math>

Generelt kan man si at:

<math> \int \frac{ax+b}{(x-x_1)(x-x_2)}dx = \int (\frac{A}{(x-x_1)}+ \frac {B}{(x-x_2)})dx

</math>

Man finner A og B slik at

Det lønner seg å velge x slik at parentesene blir lik null (en om gangen).

Det kan være lurt å huske at:

og

Eksempel 2:

<math> \int \frac{6x^2-17x+6}{x^3-5x^2+6x}dx = \int \frac{6x^2-17x+6}{x(x-2)(x-3)}dx =\int (\frac{(x-2)(x-3)A}{x}+ \frac {x(x-3)B}{x-2}+ \frac {x(x-2)C}{x-3} dx

</math>

Man må nå finne ut hva A, B og C er. Det gjør man på følgende måte

Setter først x = 0

6 = 6 A dvs. A = 1

Setter så x = 2 og får:

-4 = -2B dvs. B = 2

Setter så x = 3 og finner at C = 3. Da får man:

<math> \int \frac{6x^2-17x+6}{x^3-5x^2+6x}dx = \int \frac{6x^2-17x+6}{x(x-2)(x-3)}dx =\int (\frac{1}{x}+ \frac {2}{x-2}+ \frac {3}{x-3} dx = ln|x| + 2ln|x-2| +3ln|x-3| + C

</math>

Test deg selv

Dersom man får et intgral der teller er større enn nevner kan man prøve polynomdivisjon før integrasjon.

Polynomdivisjon før integrasjon

Dersom en polynomdivisjon ikke går opp får man en rest i form av en brøkfunksjon som er enklere enn den man startet med. Hvilke metode man bruker for å integrere denne resten er ofte delbrøkoppspalting eller variabelskifte.

Eksempel 3:

man utfører divisjonen og får

Man observere at brøken har den deriverte av nevner, i teller. Da bruker man substitusjon (variabelskifte) og får

Eksempel 4:

Utfører polynomdivisjonen og får

2= (t - 1)A + (t + 1)B

Velger t = 1 som gir B = 1

Velger så t = -1 og får A = - 1, som gir:

Utvalgte integraler

Nedenfor følger en del sentrale ubestemte integraler som er aktuelle for VG 3 - R2. Legg gjerne til integraler du tenker bør være med. Det er ofte forskjellige metoder for løsning og det nyttig å se forskjellige løsningsvarianter av samme oppgave.

$\\$

$ 1) \quad $$\int{\tan( x)}dx $

$\\$

Vi vet at $\tan\,x=\frac{\sin\,x}{\cos\,x}$ og at $\frac{d}{dx}\cos\,x=-\sin\,x$.

Vi setter $u=\cos\,x$:

<math>u=\cos\,x\,\Rightarrow\,\rm{d}u=-\sin\,x\rm{d}x</math>

Vi setter inn i integralet og får

Vi kan nå erstatte u med x igjen:

$\\$

$ 2) \quad$$\int{tan^2 (x)} dx $

$\\$

Bruker resultatet fra derivasjonen av tan(x):

$( tan(x) )' = tan^2(x) + 1 \Rightarrow \\ tan^2(x)= (tan(x))' - 1$

Vi integrerer så på begge sider

$ \int tan^2(x)dx = \int (tan(x))' -\int 1dx \\ \int tan^2(x)dx=tan(x)- x+ C$

$\\$

$ 3) \quad$$\int{ln (x)} dx $

$\\$

Vi vil integrere funksjonen $f(x)=\ln\,x$. Til det kan vi bruke et lite triks og delvis integrasjon.

Vi skriver <math>\ln\,x=1\cdot\ln\,x</math> og lar <math>u=\ln\,x</math> og <math>v'=1</math>. Da får vi

$u'= \frac{1}{x}$ og v = x. Integralet blir

Resultatet er altså at

$\int\ln |x|=x\ln\,x-x+C$

$\\$

$ 4) \quad$$\int{cos^2 (x)} dx $

$\\$

Vi prøver delvis integrasjon. ( cos x)' = - sin x og (sin x)' = cos x).

$I = \int \cos^2\,x dx = \int (\cos\,x)(\cos\,x)dx = \sin\,x \cos\,x - \int(- \sin\,x) \sin\,x dx \\ \int \cos^2\,x dx =\sin\,x \cos\,x + \int \sin^2\,x dx \\ \int \cos^2\,x dx =\sin\,x \cos\,x + \int 1 - \cos^2\,x dx \\ \int \cos^2\,x dx =\sin\,x \cos\,x + \int 1dx - \int \cos^2\,x dx \\ \int \cos^2\,x dx =\sin\,x \cos\,x + x - \int \cos^2\,x dx \\ 2 \int \cos^2\,x dx =\sin\,x \cos\,x + x \\ \int \cos^2\,x dx = \frac 12(\sin\,x \cos\,x + x) + C $

$\\$

$ 5) \quad$$\int{sin^2 (x)} dx $

$\\$

<math> \int sin^2x dx = \int (sinx \cdot sinx) dx \\ = sinx \cdot (-cosx) - \int cosx \cdot (-cosx)dx \\

= - sinx cosx + \int (1-sin^2x) dx \\ = - sinx cosx + x - \int sin^2x dx</math>

Da har man:

$\\$

$ 6) \quad$$\int{ x^2e^x} dx $

$\\$

Bruker delvis integrasjon. Setter $u =x^2$ og $v' = e^x$:

$\int x^2 e^x dx = x^2 e^x - \int 2x e^x dx$

Repeterer så øvelsen med u = 2x og får:

$\int x^2 e^x dx = x^2 e^x - \int 2x e^x dx = x^2e^x - (2xe^x - 2 \int e^x dx) \\ x^2e^x-2xe^x+2e^x + c \\ = e^x(x^2-2x+2) + c$

$\\$

$ 7) \quad $$\int{\frac{1}{x+a}}dx $

$\\$

$\\$

$ 8) \quad \int (\frac{1}{4}x^3- \frac {1}{5}x^2+2x-4)dx $

$\\$

$ \int (\frac{1}{4}x^3- \frac {1}{5}x^2+2x-4)dx= \frac{1}{16}x^4 - \frac{1}{15}x^3 + x^2 - 4x+C $

$\\$ $\\$

$ 9) \quad \int 4e^{2x+1}dx $

$\\$

Prøver integrasjon med variabelskifte, og setter

$u = 2x + 1 \\ du = 2dx\\ 4dx = 2du $

$\int 4e^{u}dx = \int 2e^{u}du = 2e^{u} + C = 2e^{2x+1} + C$

$\\$

$10) \quad \int \frac{1}{1+ \sqrt{x}}dx $

$\\$

Setter $ u = 1 + \sqrt{x } \Rightarrow \sqrt x = u-1\\ \frac{du}{dx}= \frac12x^{- \frac12} \\ du= \frac{1}{2 \sqrt{x}}dx \\ dx= 2 \sqrt{x}du \\ \int \frac{1}{u}dx = \int \frac{1}{u}2 \sqrt{x}du $

$\int \frac{1}{u}2 \sqrt{x}du \\= \int \frac{1}{u}2 (u-1)du \\= \int (2- \frac 2u)du \\= 2 \int du - 2\int \frac1u du\\ = 2u -2ln|u| + k$

Substituerer tilbake til x og får:

$ 2(1+ \sqrt x) -2ln(1 + \sqrt x) + k \\ = 2 + 2\sqrt x - 2ln(1 + \sqrt x) + k \\ = 2\sqrt x - 2ln(1 + \sqrt x)+ c $

$\\$

$11) \quad \int \sin\,(2x)\,dx $

$\\$

Setter u = 2x. $ \frac{du}{dx} = 2$

Vi får da:

$\int sin(2x) \,dx = \int sin (u) \,dx = \frac 12 \int sin(u) \,du = - \frac{1}{2}cos (2x) + c $

$\\$

$12) \quad \int (e^x-e^{-x})dx $

$\\$

$\int (e^x - e^{-x}) \, dx = e^x + e^{-x} + c$

$\\$

$13) \quad \int \frac{x}{x^2 - 4\,}dx $

$\\$

Prøver å sette $u= x^2-4$ da blir $\frac{du}{dx} = 2x$

$\int \frac{x}{x^2 - 4}\,dx = \int x \frac{1}{u} dx = \int \frac12 \frac 1u du = \frac 12 ln |x^2 - 4| +c$

$\\$

$14) \quad \int \frac{3x}{\sqrt{x^2 - 1}\,}dx $

$\\$

$u = x^2-1 \, , \, dx= \frac{du}{2x }\\ \int 3xu^{- \frac 12} \frac{du}{2x} \\ = \int \frac 32 u^{- \frac 12}du \\ = \frac 32 \cdot 2 u^{\frac 12} + c \\ =3 \sqrt{x^2-1} + c$

$15) \quad \int x^3 \cdot e^{x^2}dx $

$\\ $

$u = x^2 \, , \, dx=\frac{du}{2x} \\ \int x\cdot u \cdot e^{u} \frac{du}{2x} = \int \frac 12 ue^{u}du$

Kan nå bruke delvis integrasjon.

$\int \frac 12 ue^{u}du = \frac 12 (ue^{u} - \int e^{u}) = \frac 12( x^2 e^{x^2} - e^{x^2}) + c = \frac 12 e^{x^2}(x^2-1) + c$

$\\$

$16) \quad \int \frac{1}{x^2-3x+2}dx $

$\\$

$\int \frac{1}{x^2-3x+2}dx =\int \frac{1}{(x-1)(x-2)}dx = \int \frac{A}{x-1} + \frac{B}{x-2}dx \\ 1= A(x-2)+B(x-1)\\ x=1: \, A=-1 \\ x=2: \, B= 1 \\ \int \frac{-1}{x-1} + \frac{1}{x-2}dx \\ = -ln|x-1| + ln| x -2 | +c \\ = ln| \frac{x-2}{x-1}| + c $

$\\$

$17) \quad \int \frac{1}{x^3-3x^2+2x}dx $

$\\$

$\int \frac{1}{x^3-3x^2+2x}dx =\int \frac{1}{x(x-2)(x-1)}dx = \int ( \frac{A}{x} + \frac {B}{x-2} +\frac {C}{x-1}) dx \\ 1= A(x-2)(x-1) + Bx(x-1) + Cx(x-2) \\ x=0:\, A=\frac 12 \\ x=2:\, B = \frac 12 \\ x=1 \, C= - 1 \\ \int ( \frac{\frac 12}{x} + \frac {\frac 12}{x-2} +\frac {(-1)}{x-1}) dx \\ = \frac 12( ln|x| + ln|x-2|) - ln|x-1| +C $

$\\$

$18) \quad \int \frac{x^3+x^2+x}{x^2-1}dx $

$\\$

Her bruker vi polynomdivisjon først, og får:

$\int \frac{x^3+x^2+x}{x^2-1}dx = \int (x+1+ \frac{2x+1}{x^2-1} )dx \\ =\int (x+1+ \frac{A}{x+1} + \frac{B}{x-1}) dx \\ 2x+1=A(x-1)+B(x+1) \\ x= -1:\, -1 = -2A \Rightarrow A= \frac{1}{2} \\ x=1: \, 3=2B \Rightarrow B = \frac{3}{2} \\=\int (x+1+ \frac{\frac{1}{2}}{x+1} + \frac{\frac{3}{2}}{x-1}) dx \\ = \frac 12 x^2+x+ \frac 12 ln[x+1| + \frac 32 ln|x-1| + c \\ = \frac 12( x^2 + 2x + ln|x+1| + 3 ln|x-1| ) + c$

$\\$

$19) \quad \int \frac{1}{x^2+4x+4}dx $

$\\$

Her kan det være naturlig å teste delbrøkoppspalting, men vi får problemer med å finne A og B. Nevneren kan skrives som $(x+2)^2$ Vi prøver i stedet variabelskifte med $u= x +2$ :

$\int \frac {1}{u^2}du = \int u^{-2}du = - u^{-1} + c = - \frac{1}{x+2} +c$