R1 2023 Høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på Matteprat

Løsningsforslag laget av Realfagsportalen

REA 3056

Oppgave 1

$f(x) = x^2 \cdot ln(x)$

$f'(x) = 2x \cdot ln(x) + x^2 \cdot \frac1x = x(ln(x)+1)$

Oppgave 2

$2 \ln e^3 = 2\cdot 3 \ln e =6$

3 lg(70) Vi vet at lg 70 er mellom 1 og 2 fordi lg 10 = 1 og lg100= 2, så uttrykket er mellom 3 og 6. Vi kan omforme:

$3lg(70) = 3 lg(10 \cdot 7) = 3 (lg10 + lg 7)= 3 + 3lg 7$

$e^{3\ln2} = e^{{\ln2}^3} = 2^3 = 8$

I stigende rekkefølge:

$3 \lg(70), \quad 2 \ln e^3, \quad e^{3 \ln 2}$

Oppgave 3

a)

$\overrightarrow{AB} = [2-(-3), -2-(-1)]= [5,-1]\quad $ lengde $\sqrt{26}$

$\overrightarrow{BC}= [5-2, 2-(-2)] = [3, 4] \quad$ lengde $\sqrt{9+16} = 5$

$\overrightarrow {CA} = [-3-5), -1-2] = [-8, -3] \quad$ lengde $\sqrt {73}$

Sidekanten BC er kortest.

b)

Dersom skalarproduktet mellom vektorene er null, er vinkelen mellom dem 90 grader.

$\overrightarrow{AB} \cdot \overrightarrow{BC} = [5,-1] \cdot [3,4] = 15- 4 = 11$

$\overrightarrow{BC} \cdot \overrightarrow{CA} = [3,4] \cdot [-8,-3] = -24-12 = -36$

$\overrightarrow{CA} \cdot \overrightarrow{AB} = [-8, -3] \cdot [5, -1] = -40+ 3 = -37$

Ingen av vinklene i trekanten er 90 grader.

Del to

Oppgave 2

a)

$f(k) = k^2+(2-k)k = 2k$

$\lim\limits_{ x \to k^+} (x^2 + (2-k)x) = f(k) = 2k$

$\lim\limits_{ x \to k^-} (-x^2 + (2+k)x) = f(k) = 2k$

Funksjonene er kontinuerlig.

Oppgave 4

b)

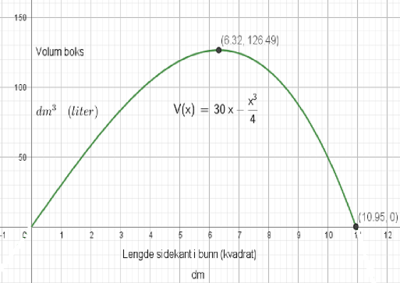
Vi setter opp et uttrykk for arealet av boksens overflate. Vi kaller sidene i grunnflaten for x og høyden for h:

$x^2 + 4xh = 120$

Bruker denne sammenhengen til å finne et uttrykk for h: $h = \frac{120-x^2}{4x}$

Finner så et uttrykk for volumet:

$V(x)= x^2 \cdot h = x^2 \cdot \frac{120-x^2}{4x} = 30x - \frac{x^3}{4}$

Det maksimale volumet boksen kan få er 126,5 liter. Da er sidekantene i bunnen ca. 63 cm.

Oppgave 6

a)

$f(x)= x^2 + 3x + 1$

$f'(x) = 2x + 3$

$f'(c) = \frac{f(b) - f(a)}{b-a} = \frac{f(3)- f(1)}{3-1} = \frac {(9+9+1) - (1+3+1)}{2} = 7$

$f'(c) = 2c+3 = 7 $

$c = 2$