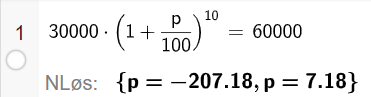2P 2022 Vår LK20 LØSNING
Diskusjon av denne oppgaven på matteprat
DEL 1
Oppgave 1
a)
Det koster totalt 25000 kr å produsere 20 stoler.
b)
Ser av grafen at det koster 5000 kr å produsere 10 stoler ekstra, det vil si at det koster 500 kr per stol. I tillegg koster det 15000 kr i konstante kostnader. Vi har $y=500x+15000$
For 120 stoler koster det $500\cdot 120 + 15000 = 60000+15000=75000$ kr.
c)
Det koster 40000 kr å produsere 50 stoler. Kostnaden per stol blir $\frac{40000}{50}=800$ kr per stol.
Oppgave 2
a)
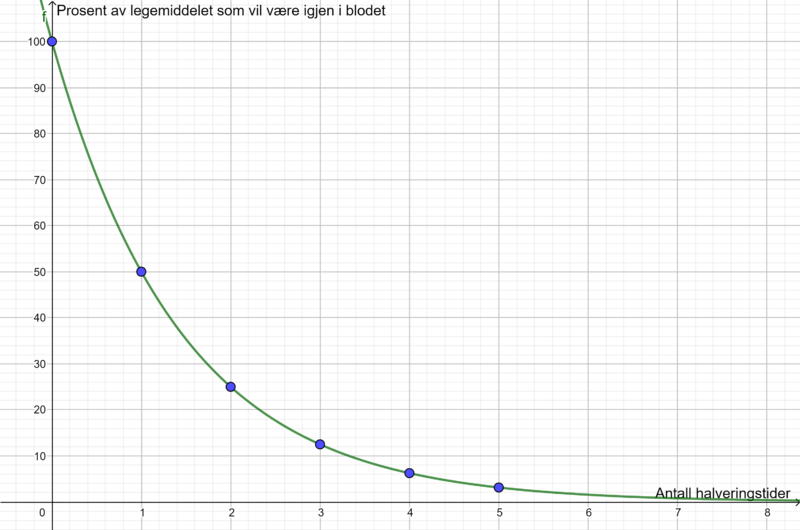
I starten : 100 %
Etter 1. halveringstid: 50 %
Etter 2 halveringstider: 25 %
Etter 3 halveringstider: 12,5 %
Etter 4 halveringstider: 6,25 %
Etter 5 halveringstider: 3,125 %
b)
Siden dette er del 1, må du tegne grafen for hånd.
Oppgave 3
Reallønna i 2015 var det samme som den nominelle lønna på 400 000 kr, siden dette er basisåret, hvor KPI er 100.
Elin har gått opp 60 000 kr i lønn fra 2015 til 2021. Det tilsvarer en 15 % økning. Utregning: $\frac{60000}{400000}= \frac{60}{400} = \frac{15}{100}= 15 $%.
Konsumprisindeksen har økt fra 100 til 116,1 i samme periode, altså en økning på 16,1%. Det betyr at levekostnadene har økt mer enn reallønna til Elin. Hun hadde altså bedre kjøpekraft i 2015 enn i 2021.
Oppgave 4
Ada ønsker å finne ut hvor mange år det tar før hun har spart 500 000 kr.
Når programmet kjøres, defineres først variablene beløp, vekstfaktor, innskudd og år (linje 1-4).
Deretter kjøres en while-løkke (linje 6-9), som gjentar seg helt til beløpet har blitt 500 000 eller større. I while-løkka økes beløpet først med 20 000 (som viser at Ada sparer 20 000 kr i året). Deretter ganges beløpet med en vekstfaktor (Ada får 2 % renter årlig). Deretter økes variabelen "år" med én, slik at vi får vite hvor mange ganger løkken har kjørt (dvs. hvor mange år Ada har spart).
Når beløpet er på 500 000 eller mer, avsluttes while-løkken, og programmet skriver ut hvor mange år som har gått, og hva beløpet er.
Oppgave 5
I området $2<x<4$, er funksjonsverdiene til andregradsfunksjonen f, mindre enn funksjonsverdiene til den lineære funksjonen g.
Ulikheten som har denne løsningen kan uttrykkes på flere måter:
$f(x)<g(x)$
$x^2−5x +5 < x − 3$
$x^2 −6x +8 < 0$
$(x − 2)(x − 4) < 0$
DEL 2
Oppgave 3
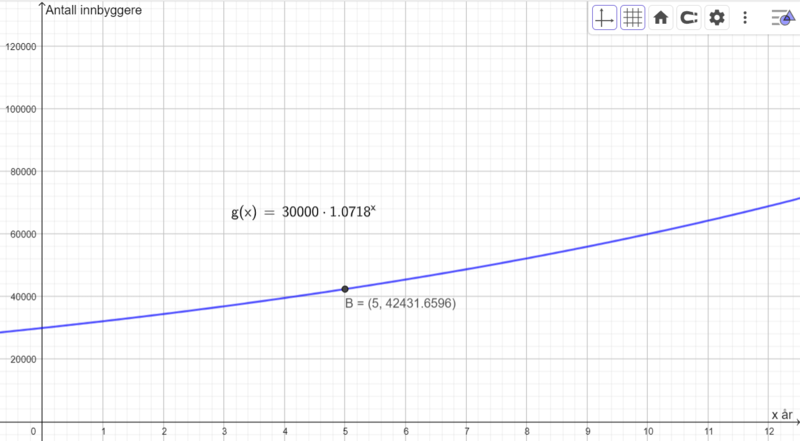
Bruker CAS i Geogebra til å finne prosent årlig vekst (det er også mulig å finne ved prøving og feiling). Finner en vekst på ca. 7,18 % per år. Vekstfaktoren blir da 1.0718, og den eksponentielle modellen blir:
$g(x)=30000\cdot 1.0718^x$
Punktet B=(5,42431) forteller oss at i starten av det 5. året, så er antall innbyggere 42431 personer, ifølge modellen.
Oppgave 5
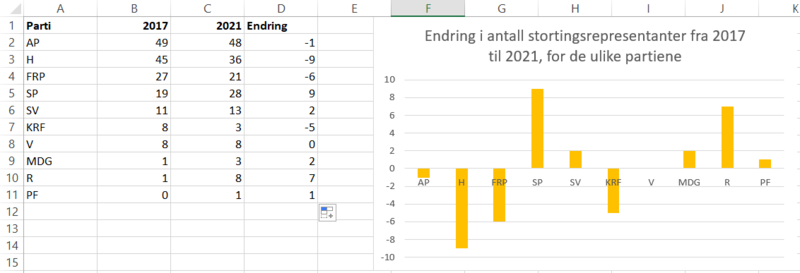
Bruker Excel til å regne ut endringen i antall stortingsrepresentanter for hvert parti fra 2017 til 2021, og til å fremstille et søylediagram som viser denne endringen. Jeg velger søylediagram fordi det er mest visuelt forklarende. Det gjør det enkelt å se endringer i antall representanter for hvert parti.
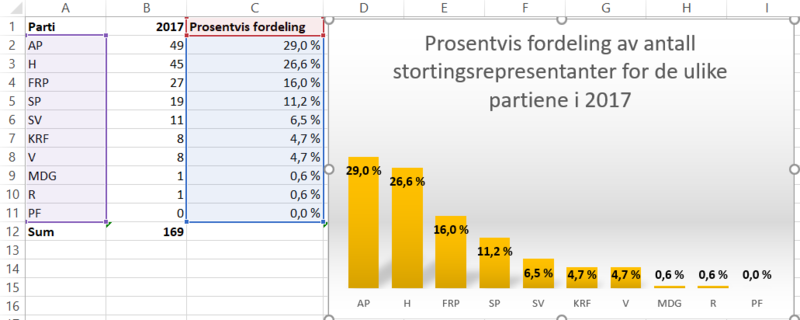
Bruker Excel til å regne ut prosentvis fordeling av representanter fra hvert parti i 2017 (ved å ta antallet i et parti, dele på det totale antall representanter, ganger 100%). Velger igjen et søylediagram, fordi jeg mener det gjør det lettest å se fordelingen. I et sektordiagram blir de minste partiene nesten ikke synlige.
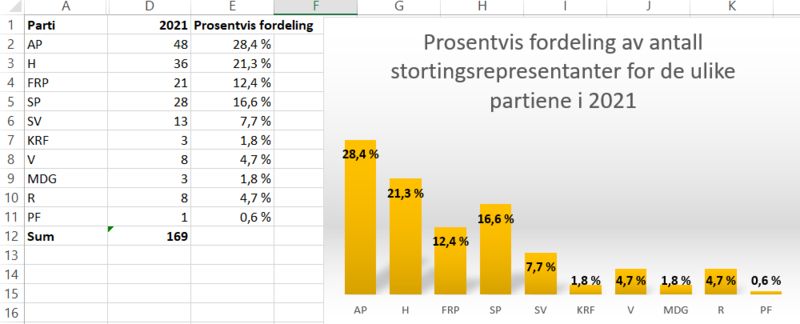
Gjentar prosessen for partiene i 2021.
Oppgave 6
a)
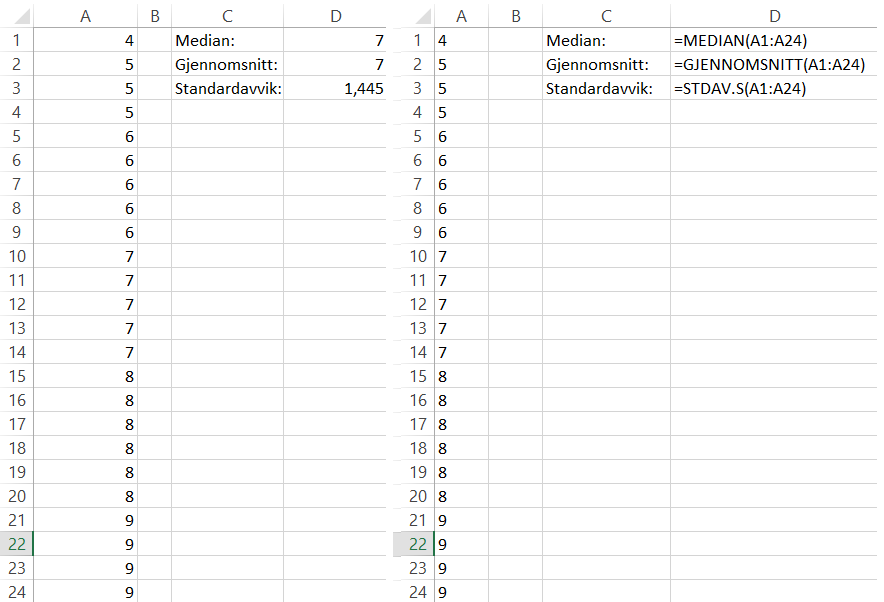
Løser oppgaven i Excel.
b)
Ola får en lavere median enn Kari, som vil si at han har kommet for sent mindre enn 7 minutter minst halvparten av gangene.
Ola får et høyere gjennomsnitt enn Kari, som vil si at han har kommet ganske mye for sent minst én gang.
Ola har et høyere standardavvik enn Kari, som vil si at antall minutter han kommer for sent avviker mer fra gjennomsnittet hans, enn det gjør for Kari.
Totalt sett kan vi si at Ola har kommet flere ganger litt for sent (under 7 minutter) enn Kari, men også har større "rekord" i antall minutter for sent enn Kari (f.eks. mer enn 10 minutter, eller enda mer).