Løsning del 2 utrinn Vår 21
Diskusjon av oppgaven på matteprat
Oppgave 1
a)
b)
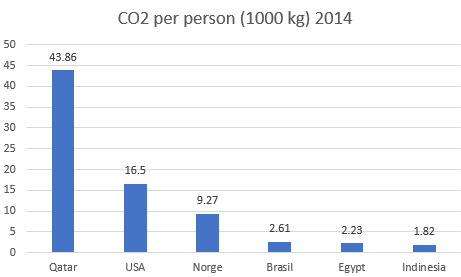
Variasjonsbredde :
c)
Nedgang i prosent fra 2014 til 2018:
Oppgave 2
a)
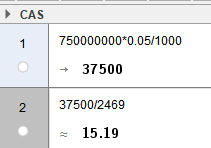
15 tonn/ min multiplisert med 60 min:
b)
Hun fikk 385 kroner i pant.
c)
Det blir et "plastfjell" ca 15 ganger høyere enn galdhøpiggen.
Oppgave 3
a)
1,9 dollar ganger 9,1245 NOK er 17 kroner og 33 ører. De som lever på dette daglig lever i ekstrem fattigdom (FN).
b)
Fra tabell og tekst ser man at 15,048 millioner utgjør 5,7% av befolkningen. Hele befolkningen blir da:
c)
Av Norges totale bistand (2017) går 0,81% til Indonesia.
Oppgave 4
a)
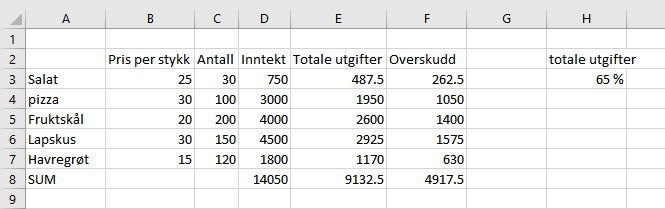
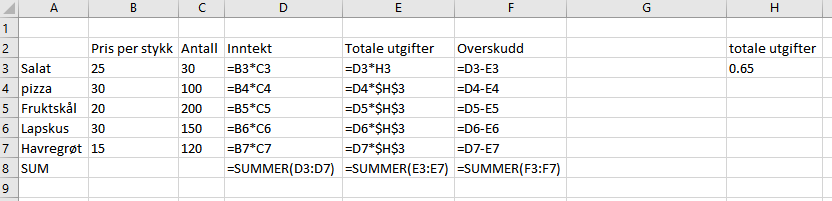
b)
Dersom utgiftene kuttes til 40% blir overskuddet 8430kr. Det er 3512,50 kr. mer enn det var før.
Oppgave 5
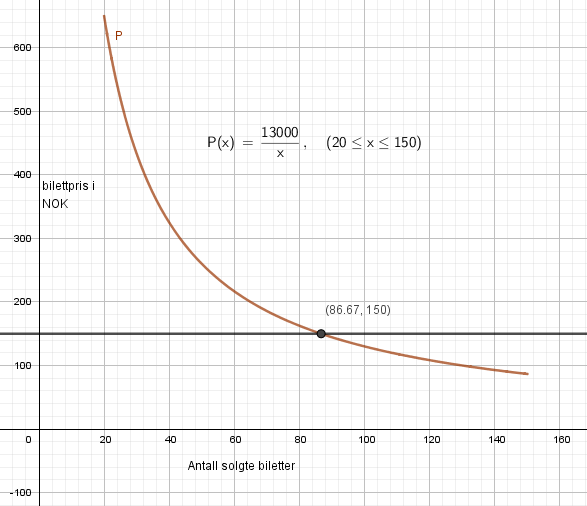
a)
b)
Som vi ser fra figuren i a, må bandet selge 87 billetter for å dekke kostnadene ved konserten.
c)
Overskuddet blir billettinntekter minus kostnader:
Oppgave 6
a)
Langs x og y retning er ikke avstanden problematisk. Det skulle være minst 360 meter mellom mølletårnene. I x og y retning er det 500 meter. Nå står det ingenting i oppgaven om tårnenes radius. Vi antar derfor at de er punkter. Langs diagonalene blir avstanden 353,6 meter. Dette er 6,4 meter mindre enn avstandskravet. I tillegg vet vi at tårnene har en utstrekning, slik at avstanden fra tårnvegg til tårnvegg blir mindre i virkeligheten. Nå må det legges til at med vindmøller i hjørnene vil parken i praksis dekke et område betydelig større enn en kvadratkilometer.
Dersom reglene er absolutte, og politikere og byråkrater har tenkt å følge dem, kan parken ikke bygges slik, selv om det var små marginer.
b)
Farten på tuppen av møllevingen:
Oppgave 7
Oppgave 8
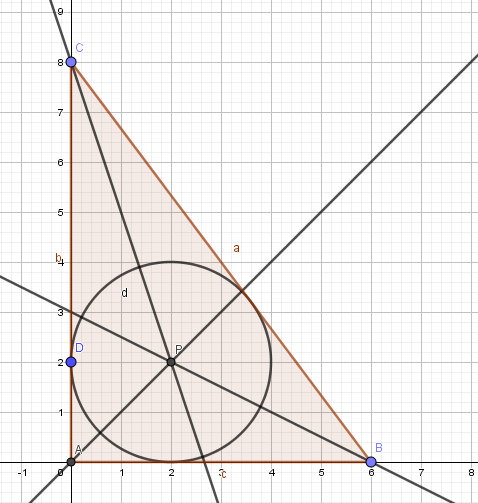
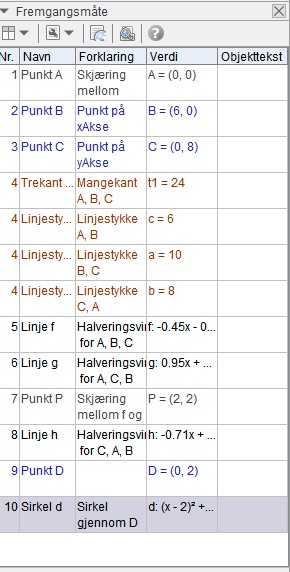
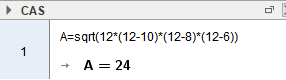
a)
Arealet av trekanten er 24.
b)
Den store trekantenc med en innskrevet sirkel, består av tre mindre trekanter, alle med høyde r. Arealet blir: