1T 2020 høst LØSNING
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
$y = 2x - 1$
Stigningstallet er 2 fordi y-verdien til funksjonen øker med 2 for hver gang x-verdien øker med 1. Konstantleddet er -1, der linjen krysser y-aksen.
Oppgave 2
$\frac{6,2\cdot10^4\cdot 2,5\cdot10^8}{0,0005} = \frac{6,2\cdot10^4\cdot2,5\cdot 10^8}{5\cdot10^{-4}} = 6,2\cdot 10^4 \cdot 0,5 \cdot 10^8\cdot 10^4 = 3,1 \cdot 10^{4+8+4} = 3,1\cdot 10^{16}$
Oppgave 3
$I. x+2y = 16 \\ II. 3x-y = 6$
Ganger likning II med 2, og legger sammen likning I og II.
$II. 3x - y = 6 \quad |\cdot 2 \\ II. 6x-2y = 12$
Likning I + II:
$ \quad\quad x+ 2y = 16 \\ + ( 6x - 2y = 12) \\ -------- \\ \quad\quad\quad\quad 7x = 28 \\ \quad\quad\quad\quad x = 4 $
Setter inn x = 4 i likning I:
$4+2y=16 \\ y = \frac{16-4}{2} \\ y=6$
Løsningen er x = 4 og y = 6. Du kan sjekke at det er riktig ved å sette inn disse verdiene i likning I og II, og se at likhetene stemmer.
Oppgave 4
$\frac{(x+y)^2-4xy}{x-y} = \frac{x^2+2xy+y^2-4xy}{x-y} = \frac{x^2-2xy+y^2}{x-y} =\frac{(x-y)^2}{x-y} = x-y$
Oppgave 5
$4x^2+kx+\frac{1}{4} = (2x)^2+kx+(\frac{1}{2})^2$
Uttrykket er et fullstendig dersom:
$kx=\pm 2\cdot 2x \cdot \frac{1}{2} \\ kx= \pm 2x \\ k = \pm 2$
Oppgave 6
$\frac{5^{\frac{1}{2}} \cdot 4^{-1} \cdot 8^{\frac{2}{3}}}{\sqrt{20}\cdot 3^0} = \frac{\sqrt{5} \cdot (2^2)^{-1} \cdot (2^3)^{\frac{2}{3}}}{\sqrt{5} \cdot \sqrt{2} \cdot \sqrt{2} \cdot 1} = \frac{2^{-2} \cdot 2^2}{2} = \frac{1}{2}$
Oppgave 7
$\frac{lg 1000 \cdot lg\frac{1}{10}}{lg 0,01 \cdot lg 10^{-\frac{1}{2}}} = \frac{3\cdot (-1)}{-2\cdot (-\frac{1}{2})} = \frac{-3}{1} = -3$
Oppgave 8
a)
$\frac{2^{2+x}}{2^{1-2x}}=64 \\ 2^{2+x-(1-2x)} = 2^6 \\ 2^{2+x-1+2x} = 2^6 \\ 2^{3x+1}=2^6 \\ 3x+1 = 6 \\ x = \frac{6-1}{3} \\ x = \frac{5}{3} $
b)
$lg(\frac{1}{x^2-3x})=-1 \\ 10^{lg(\frac{1}{x^2-3x})}=10^{-1} \\ \frac{1}{x^2-3x} = \frac{1}{10} \\ x^2-3x = 10 \\ x^2-3x-10 = 0 \\ (x+2)(x-5)=0 \\ x = -2 \vee x = 5$
Oppgave 9
- linjen $y=2x-4$ vil skjære y-aksen i x = -4, det samme som grafen til funksjonen $f$.
- linjen $y=2x-4$ vil øke med 2 enheter på y-aksen for hver enhet på x-aksen. Dermed krysser den grafen til funksjonen $f$ i punktet (5,6). Du kan vise dette ved å tegne linjen og grafen til funksjonen f i samme koordinatsystem.
- Grafen til funksjonen $f$ vil befinne seg under linjen $y = 2x-4$ når $x \in \langle 0,5 \rangle$
Vi har $f(x)<2x-4$ for $x \in \langle 0,5 \rangle$
Oppgave 10
$f(x)=x^3+3x^2+3$
$f'(x)=3x^2+6x$
$f'(x)=-3 \\ 3x^2+6x = -3 \\ 3x^2+6x+3 = 0 \quad |:3 \\ x^2+2x+1=0 \\ (x+1)(x+1)=0 \\ x=-1$
Grafen til $f$ har bare én tangent med stigningstallet -3.
Tangenten treffer funksjonen i punktet (-1, f(-1)).
$f(-1)= (-1)^3+3(-1)^2+3 = -1+3+3 = 5$
Likning for tangenten:
$y-y_1=a(x-x_1) \\ y-5 = -3(x-(-1)) \\ y -5 = -3x -3 \\ y = -3x+2$
Oppgave 11
a)
$P(\overline{C} \cap \overline{G})=P(\overline{C})\cdot P(\overline{G})= \frac{8}{10}\cdot \frac{7}{9}=\frac{56}{90}=\frac{28}{45}$
Sannsynligheten for at verken Charlotte eller Gunnar blir trukket ut er $\frac{28}{45}$
b)
$P(C \cap G) = P(C)\cdot P(G) = \frac{2}{10} \cdot \frac{1}{9} = \frac{2}{90} = \frac{1}{45}$
Sannsynligheten for at det blir Charlotte og Gunnar som skal lage kampoppsettet er $\frac{1}{45}$
Oppgave 12
a)
Bruker Pytagorassetningen til å finne lengden av BC:
$CB^2=AB^2+AC^2 \\ CB = \sqrt{1^2+1^2} \\ CB=\sqrt{2}$
$\triangle ABC$ er likebeint, og $\angle A=90^{\circ}$. De to andre vinklene må derfor være $45^{\circ} .$
Finner $sin 45^{\circ}$:
$ sin \angle ABC= \frac{AC}{BC} \\ sin 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$
Finner $cos 45^{\circ}$:
$ cos \angle ABC= \frac{AB}{BC} \\ cos 45^{\circ} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}\cdot 1}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}$
Vi har vist at $sin 45^{\circ} = cos 45^{\circ} = \frac{\sqrt{2}}{2}$
b)
Bruker arealsetningen.
$A=\frac{1}{2}\cdot PQ\cdot PR \cdot sin \angle RPQ \\ A = \frac{1}{2}\cdot 6\sqrt{2}\cdot 8 \cdot sin 45^{\circ} = 3\cdot \sqrt{2}\cdot 8 \cdot \frac{\sqrt{2}}{2} = 24 \cdot \frac{2}{2} = 24$
Arealet av trekant $\triangle PQR$ er 24.
c)
Brukes cosinussetningen:
$QR^2 = PR ^2 + PQ^2 - 2\cdot PR\cdot PQ \cdot cos \angle RPQ$
$QR^2 = 8^2+(6\sqrt{2})^2 - 2\cdot 8 \cdot 6\sqrt{2}\cdot cos 45^{\circ}$
$QR^2 = 64 + 36\cdot 2 - 96 \cdot \sqrt{2}\cdot \frac{\sqrt{2}}{2}$
$QR^2 = 64+72 - 96 \cdot 1$
$QR^2 = 40$
$QR = \sqrt{40} = \sqrt{4\cdot 10} = \sqrt{4} \cdot \sqrt{10} = 2\sqrt{10}$
Oppgave 13
Arealet av området er gitt ved $A=x\cdot y$.
Antall meter gjerde er gitt ved $x+2y=1000$. Bruker denne likningen til å uttrykket y ved x:
$x+2y=1000 \\ y=\frac{1000-x}{2} \\ y = -\frac{x}{2}+500$
Setter inn uttrykket for y i uttrykket for arealet:
$A = x\cdot y \\ A=x\cdot (-\frac{x}{2}+500) \\ A=-\frac{1}{2}x^2+500x$
Arealet er nå gitt som en andregradsfunksjon med negativt andregradsledd. Funksjonen vil følgelig ha et toppunkt. Bruker derivasjon til å finne x-verdien til dette toppunktet:
$A'(x) = -x+500$
Setter $A'(x)=0$
$-x+500 = 0 \\ x = 500$
Setter inn x=500 i uttrykket for y:
$y=-\frac{500}{2}+500 = -250+500 = 250$
Arealet blir størst mulig når x = 500 meter og y = 250 meter.
DEL 2
Oppgave 1
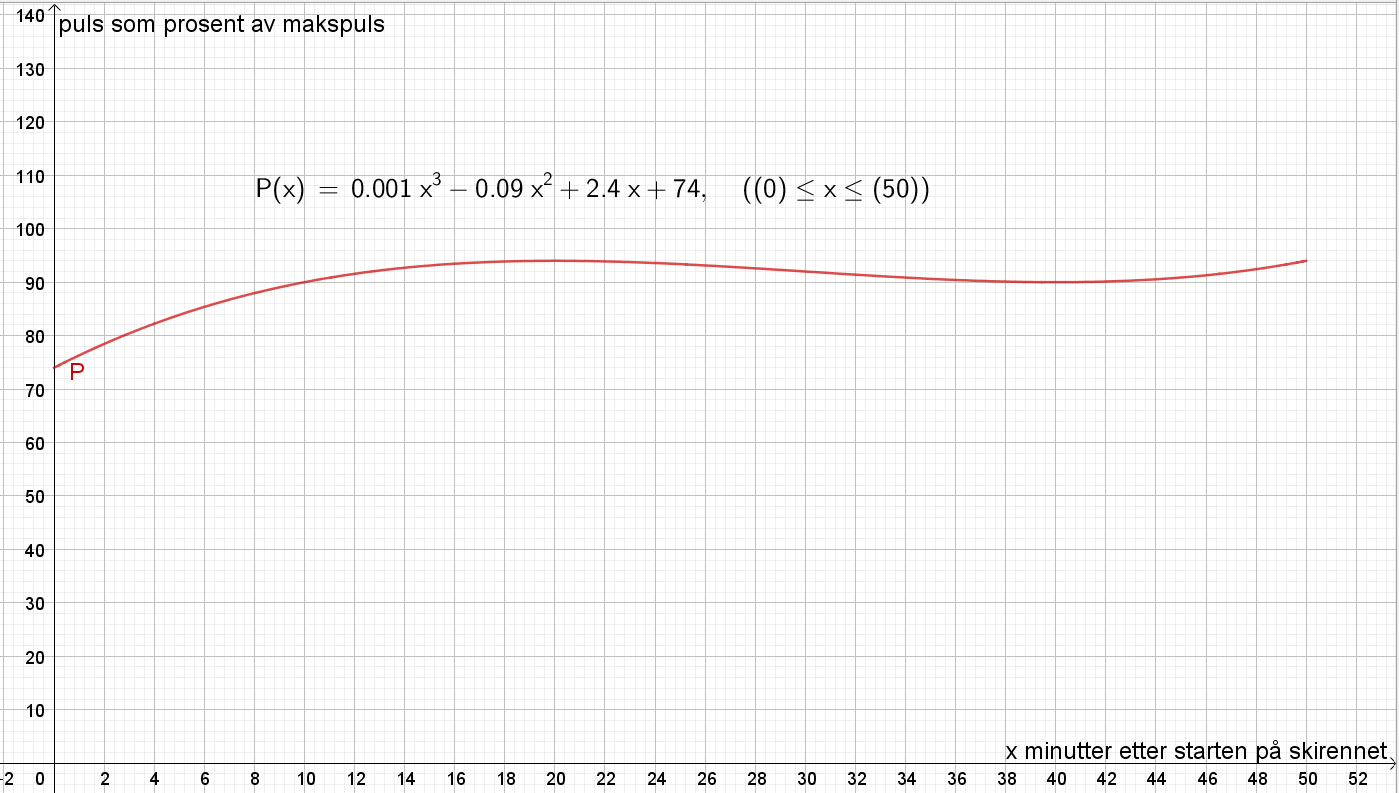
a)
b)
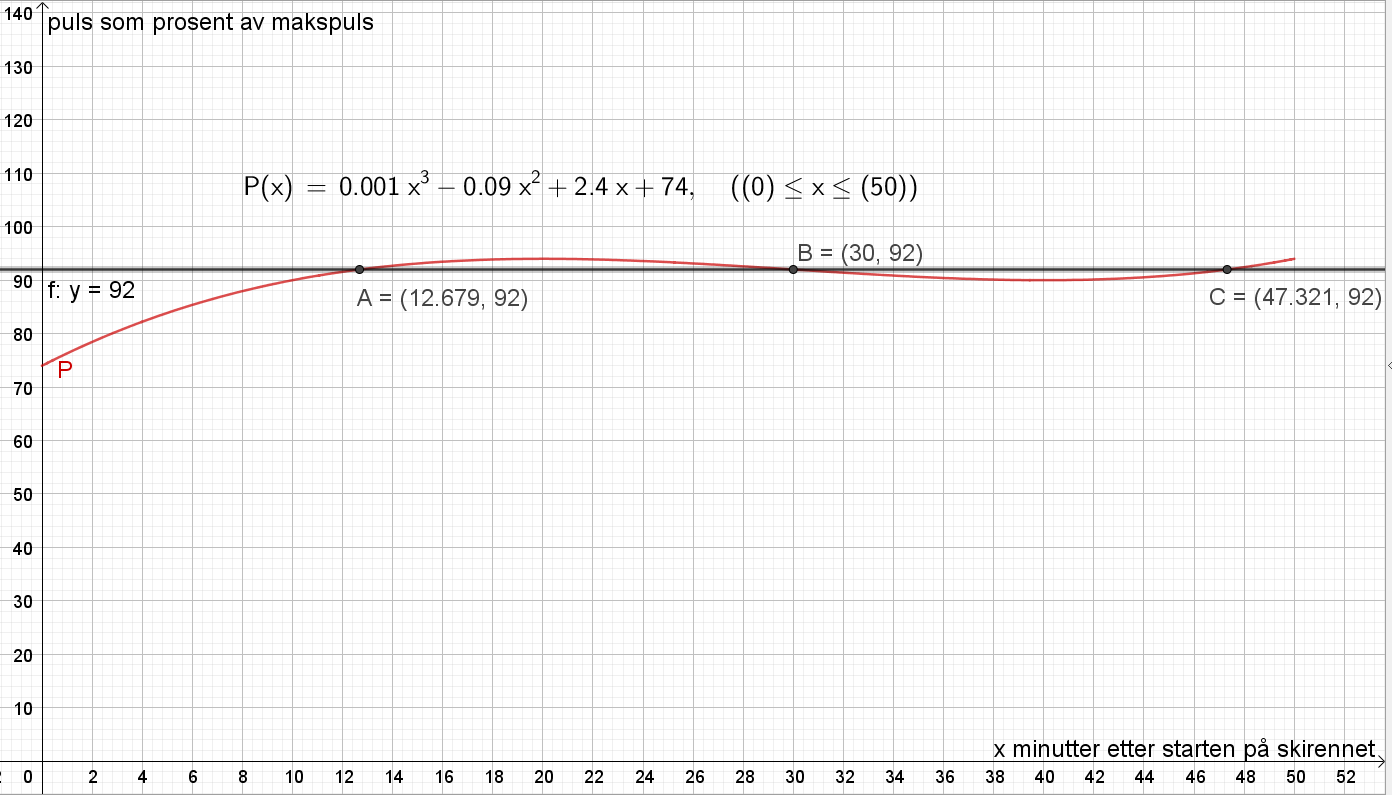
Legger inn linja y = 92, og bruker "Skjæring mellom to objekt" for å finne skæringspunktene mellom denne linjen og grafen til $P$. Leser av x-verdien til skjæringspunktene A, B og C, og beregner antall minutter hvor Ole hadde høyere enn 92% av makspuls:
$(30-12.7)+(50-47.3) = 20$
Pulsen til Ole høyere enn 92 % av makspuls i 20 minutter.
c)
Bestem den momentane vekstfarten til funksjonen når . Gi en praktisk tolkning av dette svaret.