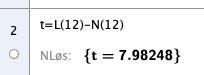1T 2019 vår LØSNING
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Løsningsforslag laget av Ole Henrik Morgenstierne
DEL EN
Oppgave 1
Oppgave 2
Vi ser at uttrykket på venstre side er et andregradsuttrykk, der grafen vender sin hule side ned. Vi er altså interessert i området mellom to eventuelle nullpunkt.
Vi faktoriser :
Nullpuktene er x= -3 og x = 1, så løsningsmengden til ulikheten er området mellom:
Oppgave 3
Oppgave 4
I denne type oppgave kan det lønne seg å prøve å faktorisere grunntallene for å minimalisere antallet grunntall.
Oppgave 5
Dette er en likebeint trekant. Normalen fra vinkelen dannet av sidene som begge er 5 vil dele grunnlinja i to like store linjestykker som hver har lengde 3. Bruker Pytagoras og ser at høyden i trekanten er 4, (
Definisjonen på tangens til en vinke er motstående katet dividert på hosliggende katet, altså:
Oppgave 6
Det hjelper å huske at
Oppgave 7
Oppgave 8
a)
Desom vi anvender abc formelen på et fullstendig kvadrat blir uttrykket under rottegnet null:
b)
Nullpunktet vil være på symmetrilinja:
Oppgave 9
a)
Hendelse M: I rute mandag - 80% Hendelse F: I rute fredag - 90%
Dersom begge henvendelsene skal inntreffe bruker vi multiplikasjonssetningen for å finne sannsynligheten:
P (M og F) =
Det er 72% sannsynlig at toget er i rute begge dagene.
b)
Dersom toget skal være i rute kun en av dagene kan det skje på to måter:
1: Toget er i rute mandag, men ikke fredag
2: Toget er i rute fredag, men ikke mandag.
P( i rute kun EN dag) =
Streken over F og M betyr sannsynligheten for at det IKKE er i rute M (mandag) eller F (fredag).
Vi får:
P( i rute kun EN dag) =
Oppgave 10
a)
b)
Fra figuren i a ser man at når det er
c)
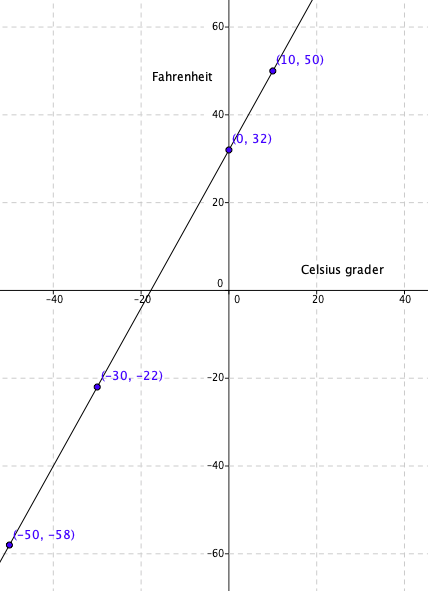
En rett linje er gitt som y= ax + b
I dette tilfelle er x = C og y = F, b = 32
Vi får da: F = aC + 32
For å finne stigningstallet, a, bruker vi de to siste punktene gitt i oppgaven ( 0, 32) og (10, 50). Man kan bruke hvile to punkter man vil men det lønner seg alltid å velge verdier som gir enklest mulig regning. Vi tar endring i y verdi delt på endring i x verdi:
d)
Altså er
Oppgave 11
a)
1)
2)
b)
Vi vet at definisjonen på cosinus i en rettvinklet trekant er hosliggende katet delt på hypotenus. Fra ungdomskolen vet vi at i en 30 - 60 - 90 trekant er det korteste katetet halvparten så lang som hypotenusen. Dersom vi lager en 30-60-90 trekant med hypotenusene lengde lik 1 får vi:
c)
Vi bruker Cosinussetningen for å finne BC:
Så benytter vi resultatene fra oppgave a:
Oppgave 12
Arealet er gitt: A = 12. Arealsetningen gir
Oppgave 13
Vi deler figuren opp.
Vi har tre fjerdedeler av en sirkel med radius 3a
Vi har en linje med lengden 2a og en linje med lengden 3a. For å finne lengden av den tredje linjen, den som går på skrå i koordinatsystemet, bruker vi Pytagoras. Den endrer seg 3a i x retning og 4a i y retning:
Omkretsen blir da:
Oppgave 14
Den deriverte av p i null lik null stemmer for A og D. Den deriverte av p i -1 skal vare negativ, stemmer bare for A. Derfor er A grafen til p.
Vi ser at graf E har en konstant stigning lik -2 (altså synker den med to for hver enhet av x) og er den eneste som passer til betingelsene til q. Altså viser E grafen til funksjonen q.
Når vi beveger oss fra -2 til 0 på x aksen har vi beveget oss to enheter. Dersom den gjennomsnittlige veksten skal bli 3 må endringen på y aksen være 6 (
Begge tangentene har stigningstall -8 når x=-2 og x=2. Det betyr at funksjonen avtar. Det passer kun med B. B er grafen til s.
DEL TO
Oppgave 1
a)
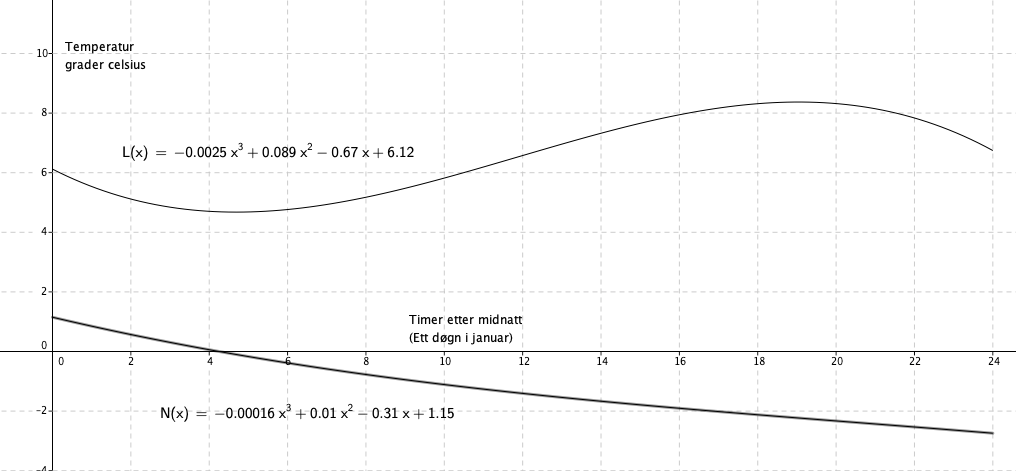
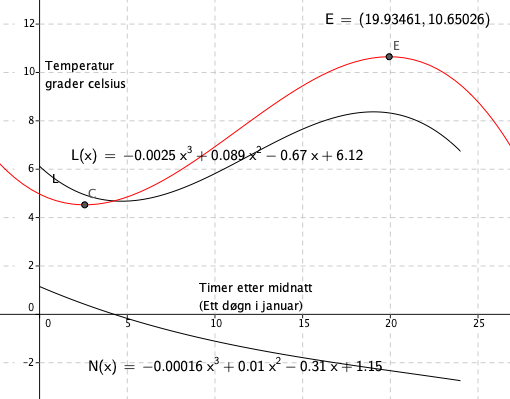
L er temperatur på Lindesnes
N er temperatur på Nordkapp
b)
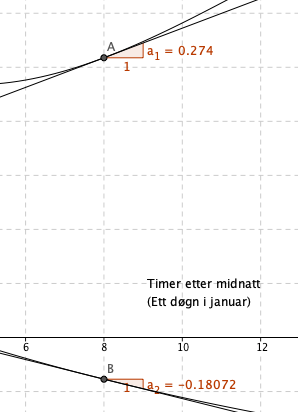
Når klokken er 8 på morgen øker temperaturen på Lindesnes med 0,27 grader per time. På Nordkapp synker den med 0,18 grader.
Jeg la inn to tangenter for x=8. Stigningstalle til disse er grafenes momentane vekst.
c)
Temperaturforskjellen kl 12:00 var nesten 8 grader celsius.
d)
Laget en funksjon som viser temperaturforskjellen: L(x) - N(x). Den har toppunkt ca kl 20:00. Da er temperaturforskjellen ca 10,7 grader.
Oppgave 2
a)
Krysstabell:
| under tredve | over tredve | Sum | |
| kildesorterer | 365 | ||
| kildesorterer ikke | 635 | ||
| Sum | 250 | 750 | 1000 |
b
c)
Oppgave 3
a)
f(x) = ax + b
Siden vi beveger oss en møt høyre på x aksen vil lengden av linjestykket BC tilsvare stigningstallet til den rette linjen, altså a.