Løsning del 2 utrinn Vår 19
Løsningsforslag lagt ut på Facebookgruppen Matematikkdidaktikk
Oppgave 1
a)
b)
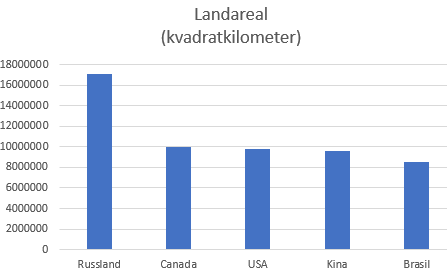
Variasjonsbredden er største minus minste verdi:
17 098 240 $km^2$ - 8 515 770 $km^2$ = 8 582 470 $km^2$
c)
".... enn arealet av Brasil." Betyr at det er arealet av Brasil man skal sammenligne med:
$\frac{17098240}{8515770} \cdot 100$ % = 200,78%. Siden Brasil utgjør 100 av disse prosentene er Russland 100,78% større enn Brasil
Oppgave 2
a)
Vi avleser y aksen og ser at grafen slutter på ca. 6200 km.
b)
Vi ser at mellom 1 og 6 timer er grafen parallell med x aksen, hvilket betyr at avstanden fra Oslo ikke endrer seg, dvs. hun har en pause på fem timer.
c)
Vi ser fra kartet at New York ligger seks timer etter Oslo. I Oslo er klokka 18:55 når hun lander, det betyr at klokka i New York er 12:55.
Oppgave 3
a)
$2 \cdot 27 + 22 = 76$ GBP
Multiplisert med 11 blir det ca. 836 NOK.
b)
377m = 0,377 km
30 min = 0,5 h
$0,377 : 0,5 = 0,754 $km/h
c)
Forholdet mellom lengde og høyde er 5:3. Dersom lengden til et flagg er 7,5 m er høyden $ \frac{7,5m}{5} \cdot 3 = 4,5 m$
Bredden på stripen er $\frac 15$ av dette, altså $\frac{4,5}{5} = 0,9 m.$
Oppgave 4
a)
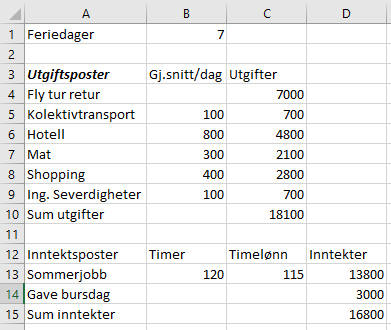
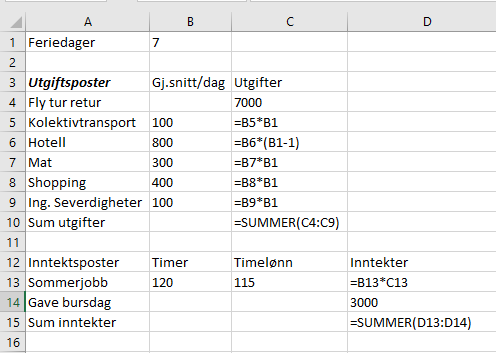
Prisen på overnatting er multiplisert med seks fordi syv dagers ferie krever seks overnattinger.
b)
Hun mangler 1300 kroner og må jobbe $1300 : 115 = 11,3$. Hun må jobbe 12 timer til, altså totalt 132 timer.
Oppgave 5
a)
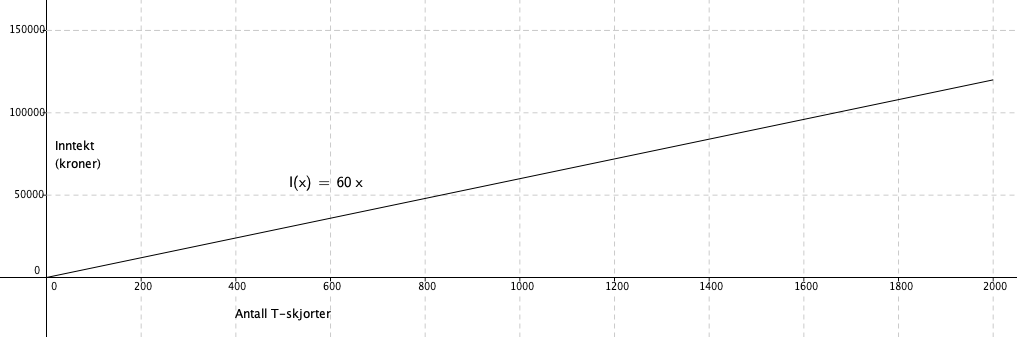
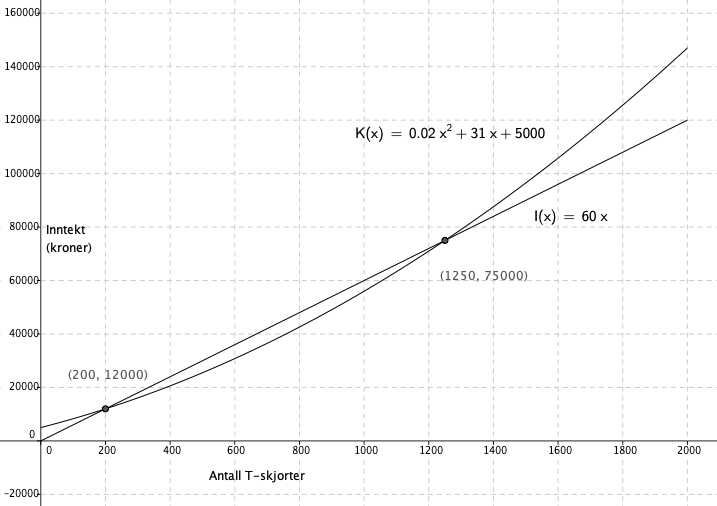
Prisen for en T - skjorte er 60 kroner.
b)
c)
d)
For at inntektene skal være større enn kostnadene må salget være mer enn 200 og mindre enn1250 T - skjorter. Se figur i c.
Oppgave 6
a)
$365:29,5= 12$
Månen går 12 hele runder rundt jorda i løpet av et år.
b)
$O = 2 \pi \cdot \sqrt{0,5\cdot (a^2 + b^2)} = \\ 2 \pi \cdot \sqrt{0,5\cdot (405000^2 + 363000^2)} = \\ 24.166.348 km$
Omkretsen er ca. 24,2 millioner kilometer.
Oppgave 7
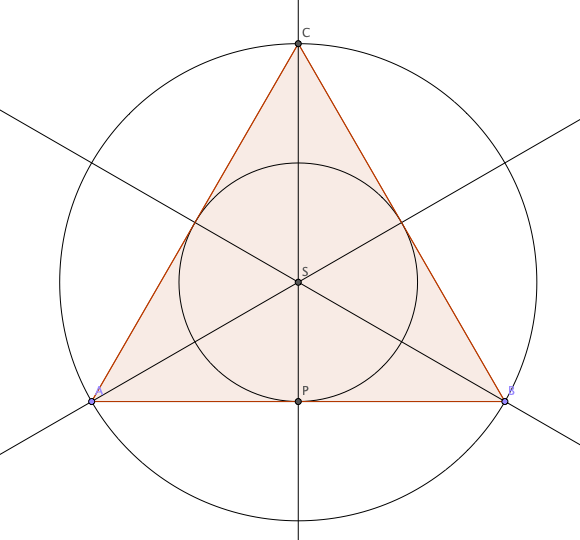
Her er et forslag av mange mulige løsninger.
Avsatte AB 10 cm. Laget regulær trekant. Halverte vinklene for å finn S. Slo den omskrevne sirkelen. Fant P og slo den innskrevne sirkelen.
Oppgave 8
Denne oppgaven minner sterkt om oppgave 7. Mulig vi kan dra nytte av å ha løst den.
a)
O= 24901,5 mile $\cdot $ 1,60934 km/ mile = 40074,98 km, som skulle vises.
b)
$O = 2 \pi r \\ r = \frac{O}{2 \pi} \\ r= \frac{40075 km}{2 \pi} \\ r = 6378 km$
c)
Satelittenes banehøyde blir radius i den indre sirkelen (jorda) minus radius i den ytre sirkelen (satelittbanen). Vi trekker linjen AS og normalen fra S på AB. Da får vi en 30, 60, 90 trekant. Hypotenusen er da dobbelt så stor som minste katet. Minste katet er jordradius. Høyden til satelittbanen er like lang som jordradius, altså ca 6378 km over jordens overflate.
Oppgave 9
a)
I en kvadratisk grunnflate er alle sidene like lange.
$ \sqrt{1225 m^2} = 35m$
b)
Finner først avstanden fra toppen av pyramiden, til midt nede på sidekanten (hs). Finner så arealet av en side, og multipliserer med fire.
$hs = \sqrt{(21,65m)^2 + (17,5m)^2} = 27,84$
Arealet av en sideflate blir da
$ \frac{35m \cdot 27,84m}{2} = 487,17 m^2$
Og arealet av hele overflaten blir
$ 4 \cdot 487,17 m^2 = 1948,68m^2 \approx 1950 m^2$
c)
Volum av glass:
$V = 1948,68 m^2 \cdot 0,02152 m = 41,94 m^3 \approx 42m^3$
Massen blir da:
$42m^3 \cdot 2400 \frac{kg}{m^3} = 100 800 kg$ eller 100,8 tonn.