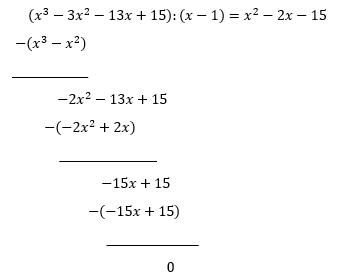S2 2018 vår LØSNING

oppgave som pdf

Diskusjon av denne oppgaven på matteprat

Løsning laget av mattepratbruker Tommy O.

DEL 1

Oppgave 1

a)

$f(x)=2x^3-4x+1 \\ f'(x) = 6x^2 - 4$

b)

$g(x)=\frac{x}{e^x}$

$g'(x)= \frac{1 \cdot e^x - x \cdot e^x}{(e^x)^2} = \frac{e^x (1-x)}{(e^x)(e^x)} = \frac{1-x}{e^x} $

c)

$h(x)=ln(x^2+4x) \\ g(u)=ln(u), \quad u=x^2+4x \\ h'(x)=g'(u)\cdot u'(x)=\frac{1}{u} \cdot u' =\frac{2x+4}{x^2+4x}$

Oppgave 2

$ I \quad \, 5x+y+2z=0 \\ II \,\,\,\, 2x+3y+z=3 \\ III \, 3x+2y-z=-3$

Legger sammen likning II og III.

$2x+3x + 3y + 2y + z-z = 3 -3 \\ 5x+5y=0 \\ x+y=0 \\ x=-y$

Setter inn $x=-y$ i likning I.

$5\cdot (-y)+y+2z=0 \\ -4y+2z=0 \\ 2z=4y \\ z=2y$

Setter inn $z=2y$ og $x=-y$ i likning II.

$2\cdot (-y)+3y+2y=3 \\ 3y=3 \\ y=1$

$x=-y=-1$

$z=2y=2\cdot 1=2$

Løsning: $x=-1,\,y=1,\,z=2$

Oppgave 3

a)

$P(x)=x^3-3x^2-13x+15$

$P(1)=1^3-3\cdot 1^2-13\cdot 1+15= 1-3-13+15=0$

x=1 er et nullpunkt, så P(x) er delelig med (x-1).

b)

Utfører polynomdivisjon for å faktorisere P(x)

Resten faktoriseres: $x^2-2x-15=(x^2-5x+3x+(-5)\cdot 3)=(x-5)(x+3)$. Bruk andregradsformelen ved behov.

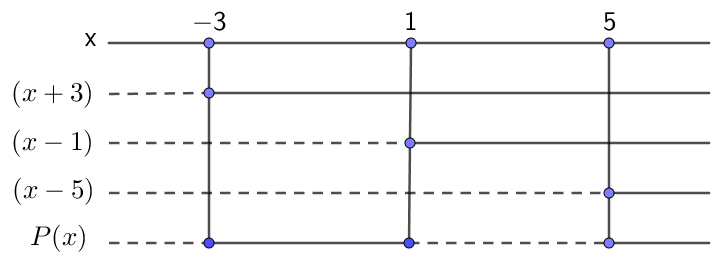
Vi har $P(x)=(x-5)(x-1)(x+3)$. Bruker fortegnsskjema for å løse ulikheten.

$P(x)>0$ når $-3<x<1$ og $x>5$.

Løsningen kan også skrives som $x \in \langle -3,\,1 \rangle$ og $x \in \langle 5,\, \rightarrow \rangle$

Oppgave 4

a)

Differansen, d, mellom to ledd i en aritmetisk rekke er konstant. Finner d:

$a_4=a_1+d+d+d \\ 14=2+3d \\ 3d=12 \\ d=4$

n	1	2	3	4	n
$a_n$	2	6	10	14
Formel	$2+4\cdot 0$	$2+4\cdot 1$	$2+4\cdot 2$	$2+4\cdot 3$	$2+4\cdot (n-1)=4n-2$

$a_n=4n-2$

b)

Summen av en aritmetisk rekke er gitt ved:

$S_n=\frac{a_1+a_n}{2} \cdot n$

Finner $a_{100}$:

$a_{100}=4\cdot 100-2=398$

Regner ut summen av de 100 første leddene i vår rekke:

$S_{100}=\frac{2+398}{2} \cdot 100 = 200 \cdot 100 = 20000$

Oppgave 5

a)

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer. I slike tilfeller er $S_n=\frac{a_1}{1-k}$ når n går mot uendelig.

Her har vi $a_n=3\cdot (\frac{1}{4})^{n-1}$. Siden $-1<k<1$, så konvergerer rekken.

Regner ut summen av rekken når n går mot uendelig:

$S_n=\frac{3}{1-(\frac{1}{4})} = \frac{3}{\frac{3}{4}} = \frac{3\cdot 4}{3} = 4$

b)

$0,242424...=0,24+0,0024+0,000024+...=\frac{24}{100}+ \frac{24}{100^2}+\frac{24}{100^3}+...$

Dette er en geometrisk rekke hvor

$a_n=\frac{24}{100}\cdot (\frac{1}{100})^{n-1}$

Siden $-1<k<1$, konvergerer rekken. Summen av denne rekken når n går mot uendelig er:

$S_n=\frac{\frac{24}{100}}{1-\frac{1}{100}}=\frac{\frac{24}{100}}{\frac{99}{100}}=\frac{24}{99}$

Det betyr at $0,242424...$ kan skrives som $\frac{24}{99}$

Oppgave 6

a)

$f(x)=\frac{6}{1+e^{-x}}$

Bruker kvotientregelen for derivasjon.

$f'(x)=\frac{0 \cdot (1+e^{-x})-6 \cdot (-e^{-x})}{(1+e^{-x})^2} = \frac{6e^{-x}}{1+2e^{-x}+e^{-2x}}$

Alle potenser av $e$ er positive (og større enn 0). Både telleren og nevneren til $f'(x)$ er altså positive. En brøk med positiv teller og nevner har alltid positiv verdi. Altså er $f'(x)>0$ for alle verdier av x. Det vil si at $f(x)$ er strengt voksende.

b)

Finner grenseverdien av f(x) når x går mot uendelig:

$lim_{x \rightarrow \infty} e^{-x}=0$

Det vil si at når x går mot uendelig, går $e^{-x}$ mot null. Følgelig har vi at:

$lim_{x \rightarrow \infty} \frac{6}{1+e^{-x}}=\frac{6}{1+0}=6$

Finner grenseverdien av f(x) når x går mot minus uendelig:

$lim_{x \rightarrow - \infty} e^{-x}=e^{\infty}=\infty$

Det vil si at når x går mot minus uendelig, går $e^{-x}$ mot uendelig. Følgelig har vi at:

$lim_{x \rightarrow - \infty} \frac{6}{1+e^{-x}}=\frac{6}{\infty}=0$

Altså er $0<f(x)<6$.

c)

Bruker kvotientregelen for derivasjon.

$f ' '(x) = \frac{(-6e^{-x})(e^{-2x}+2e^{-x}+1)-(6e^{-x})(-2e^{-2x}-2e^{-x})}{(e^{-2x}+2e^{-x}+1)^2} \\ = \frac{-6e^{-3x}-12e^{-2x}-6e^{-x}+12e^{-3x}+12e^{-2x}}{(e^{-2x}+2e^{-x}+1)^2} \\ = \frac{6e^{-3x}-6e^{-x}}{(e^{-2x}+2e^{-x}+1)^2}$

Brøken kan forkortes videre, men vi behøver ikke det. Vi skal finne x-verdien hvor $f ' '(x)=0$, og trenger bare å se på telleren videre. Nevneren er et kvadrat av et uttrykk som alltid er større enn 0. Nevneren er derfor alltid større enn 0.

Vi har $f ' '(x)=0$ når $6e^{-3x}-6e^{-x}=0$.

$6e^{-3x}=6e^{-x} \\ e^{-3x}=e^{-x} \\ -3x=-x \\ x=0$

$f(x)$ har et vendepunkt i x=0. Finner y-verdien:

$f(0)=\frac{6}{1+e^{-0}}=\frac{6}{1+1}=3$

$f(x)$ har et vendepunkt i $(0,3)$.

d)

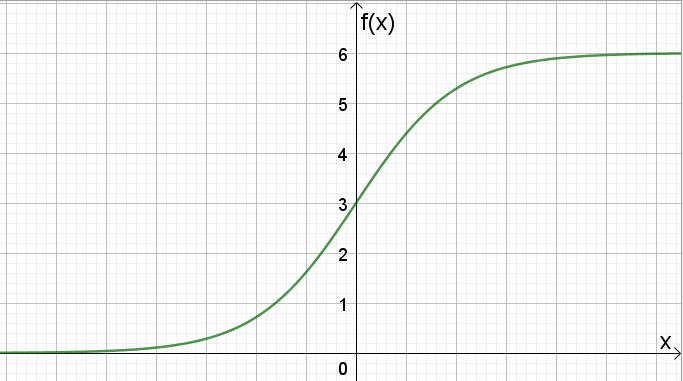
Vi vet at $0<f(x)<6$ og at vi har et vendepunkt i $(0,3)$. Vi vet også at dette er en logistisk funksjon, som er S-formet. Vi vet ikke så mye om x-aksen, men kunne eventuelt regne ut noen av punktene. Skisse av funksjonen:

Oppgave 8

a)

$x=1,10 \Rightarrow z=\frac{x-\mu}{\sigma}=\frac{1,10-1}{0,05}=\frac{0,10}{0,05}=\frac{10}{5}=2$

$x=0,90 \Rightarrow z= \frac{0,90-1}{0,05}=\frac{-0,10}{0,05}=\frac{-10}{5}=-2$

$P(0,90 \leq X \leq 1,10)=P(-2 \leq Z \leq 2)=P(Z \leq 2)-P(Z \leq -2) = P(Z \leq 2)-(1-P(Z \leq 2)) \\ 0,97725-(1-0,97725) = 0,97725-0,02275=0,95450$

Sannsynligheten for at et tilfeldig valgt rugbrød veier mellom 0,90 kg og 1,10 kg er 95,45%.

b)

$\mu_S=n\cdot \mu_x=100\cdot 1,00\,kg=100\,kg$

$\sigma_S=\sqrt{n} \cdot \sigma_x=\sqrt{100}\cdot 0,05\,kg=10\cdot 0,05\,kg=0,5\,kg$

$S=100,5 \Rightarrow z=\frac{100,5-100}{0,5}=\frac{0,5}{0,5}=1$

$S=99,5 \Rightarrow z=\frac{99,5-100}{0,5}=\frac{-0,5}{0,5}=-1$

$P(99,5 \leq S \leq 100,5)=P(-1 \leq Z \leq 1)=P(Z \leq 1)- (1-P(Z\leq 1)) \\=0,84134-(1-0,84134)=0,84134-0,15866=0,68268$

Sannsynligheten for at veksten av rugbrødene på en tilfeldig pall er mellom 99,5 kg og 100,5 kg er ca. 68,3%.

Oppgave 9

$g(x)=-5 \cdot f(x)+3$

$g'(x)=-5\cdot f'(x)$. Det vil si at dersom $f'(x)=0$, så er $g'(x)=0$. $f(x)$ og $g(x)$ har derfor samme ekstremalpunkter. Derimot vil grafen til g synke når grafen til f stiger og omvendt, fordi $g'(x)$ alltid har motsatt fortegn som $f'(x)$.

Et toppunkt for f er $(2,3)$

$g(2)=-5\cdot f(2)+3=-5\cdot 3+3=-15+3=-12$

$g(x)$ har et bunnpunkt i $(2,-12)$.

Et bunnpunkt for f er $(3,-4)$

$g(3)=-5\cdot f(3)+3= -5\cdot (-4)+3=20+3=23$

$g(x)$ har et toppunkt i $(3,23)$.

DEL 2

Oppgave 1

a)

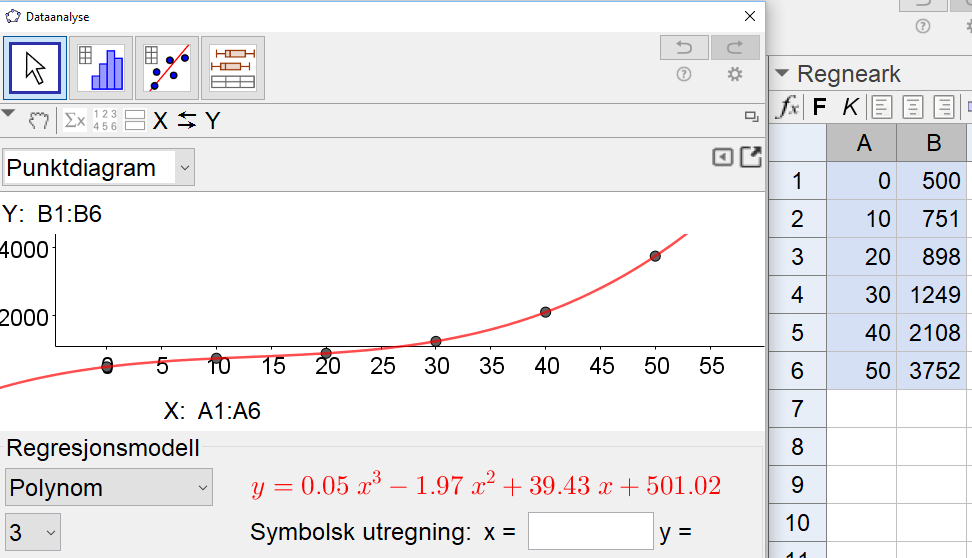
Bruker Geogebra til å utføre en regresjonsanalyse på punktene i tabellen. Velger polynomfunksjon av 3. grad som modell for kostnadene, h(x). Se skjermbildet under.

Jeg har funnet en modell for kostnaden, $h(x)=0,05x^3-1.97x^2+39,43x+501,02$

Inntekten er 80 kroner per enhet, og kan uttrykkes som $I(x)=80x$.

For å finne en modell for overskuddet, O(x), bruker jeg CAS i Geogebra, og regner ut O(x)=I(x)-h(x). Se skjermbildet under.

Jeg har dermed vist at funksjonen $O(x)=-0,05x^2+2,0x^2+41x-501$ (noe avrundet) er en god modell for det daglig overskuddet til bedriften ved produksjon av x enheter.