S1 2018 høst LØSNING
Diskusjon av denne oppgaven på matteprat
Løsning laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
b)
c)
Oppgave 2
a)
b)
Jeg synes dette svaret er penest, men man kan også skrive svaret slik:
Oppgave 3
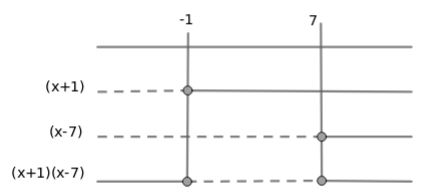
Løser likningen
Et andregradsuttrykk
Faktoriserer andregradsfunksjonen:
Lager fortegnsskjema:
Svar:
Alternativt kan svaret skrives slik:
Velg din favoritt!
Oppgave 4
a)
b)
Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel:
Sannsynligheten for at det blir trukket ut to jenter og to gutter er
c)
P(minst en gutt) = 1 - P(ingen gutter) =
Sannsynligheten for at minst én gutt fra elevrådet blir med på turen er
Oppgave 5
a)
Trekker likning II fra likning I og får:
Setter inn
Løsning:
b)
Uttrykker de to første ulikhetene med hensyn på y:
Ulikhet nr. 1:
NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.
Ulikhet nr. 2:
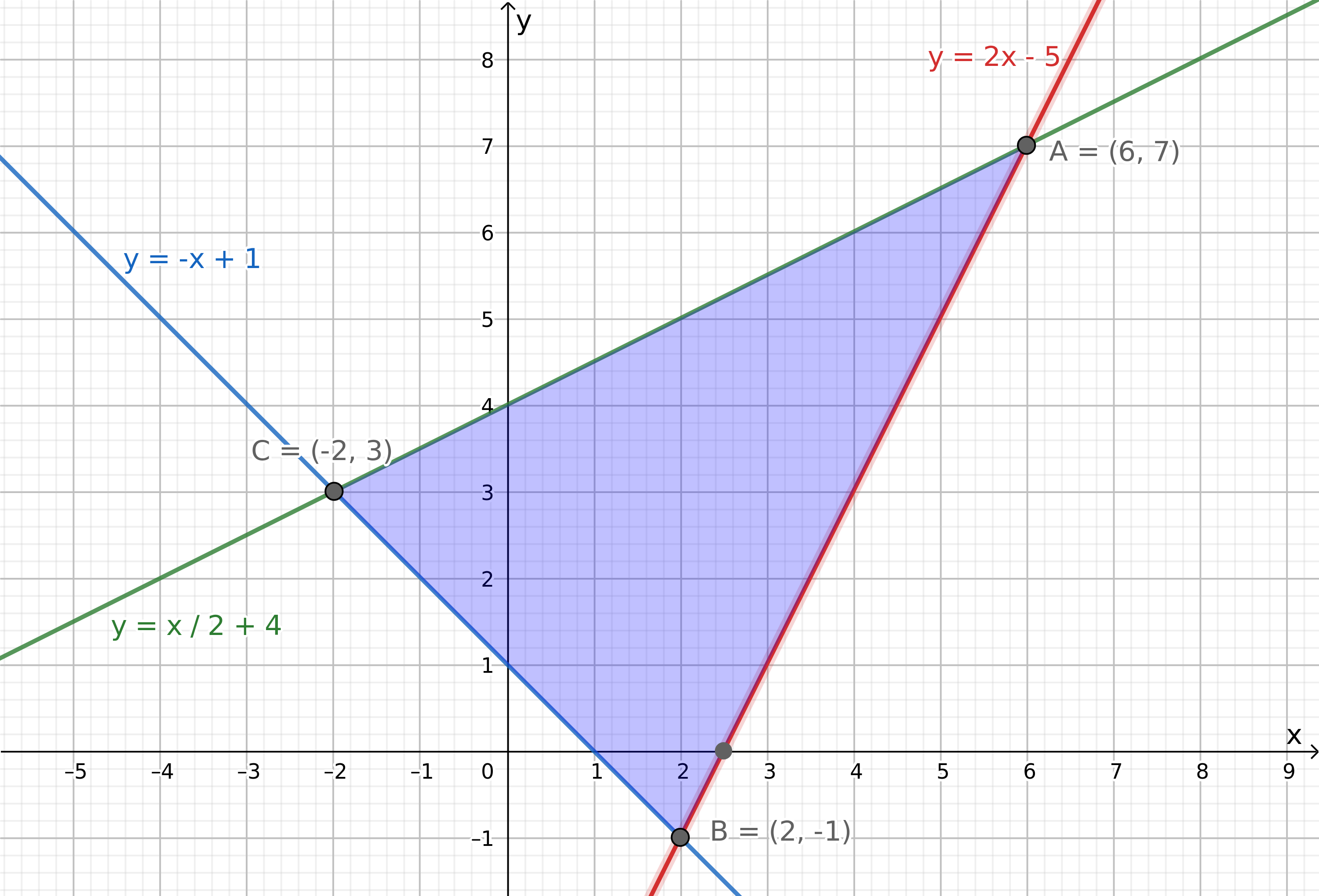
Vi har nå de tre ulikhetene:
Tegn de tre linjene
c)
Sjekker verdien til
Punkt A:
Punkt B:
Punkt C:
Størrelsen
Oppgave 6)
a)
Setter
Siden O er en andregradsfunksjon med negativt andregradsledd, vet jeg at funksjonen har et toppunkt, og ikke et bunnpunkt. Den produksjonsmengden som gir størst overskudd er 20 enheter per dag. Finner overskuddet
Overskuddet blir 25 000 kr.
b)
Setter
Det vil bli overskudd for en daglig produksjon mellom 10 og 30 enheter. Siden O er en andregradsfunksjon med toppunkt på x=20, vet jeg at funksjonen har en positiv verdi fra x=10 til x=30.
Oppgave 7
a)
Leser av de aktuelle punktene grafisk: (-1,5) og (2,8).
Gjennomsnittlig vekstfart i intervallet [-1,2]:
Gjennomsnittlig vekstfart i intervallet [-1,2] er 1.