S1 2018 vår LØSNING
Løsning laget av mattepratbruker Tommy O.
Løsning laget av LektorNilsen (pdf)
diskusjon av oppgaven på matteprat
DEL1
Oppgave 1
a)
Bruker abc-formelen
b)
c)
Oppgave 2
Løser likning to med hensyn på y:
Bruker innsettingsmetoden og erstatter y med 3x-1 i likning én.
Bruker abc-formelen
Bruker likning to for å finne tilhørende y-verdier:
Løsning:
Oppgave 3
a)
b)
c)
Oppgave 4
Kjenner igjen likningen
Et andregradsuttrykk
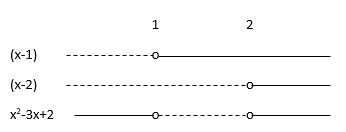
Faktoriserer uttrykket:
Lager fortegnsskjema:
Løsning:
Oppgave 5
a)
b)
Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel:
P(tre blå kuler)=
Sannsynligheten for at du trekker 3 blå kuler er
c)
Dersom du skal trekke både røde og blå kuler, må du trekke enten én blå og to røde, eller to blå og én rød.
P(både røde og blå kuler) = P(én blå og to røde)+P(to blå og én rød)
Sannsynligheten for at du trekker både røde og blå kuler er
Oppgave 6
Uttrykker de to siste ulikhetene med hensyn på y:
Ulikhet nr. 3:
Ulikhet nr. 4:
NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.
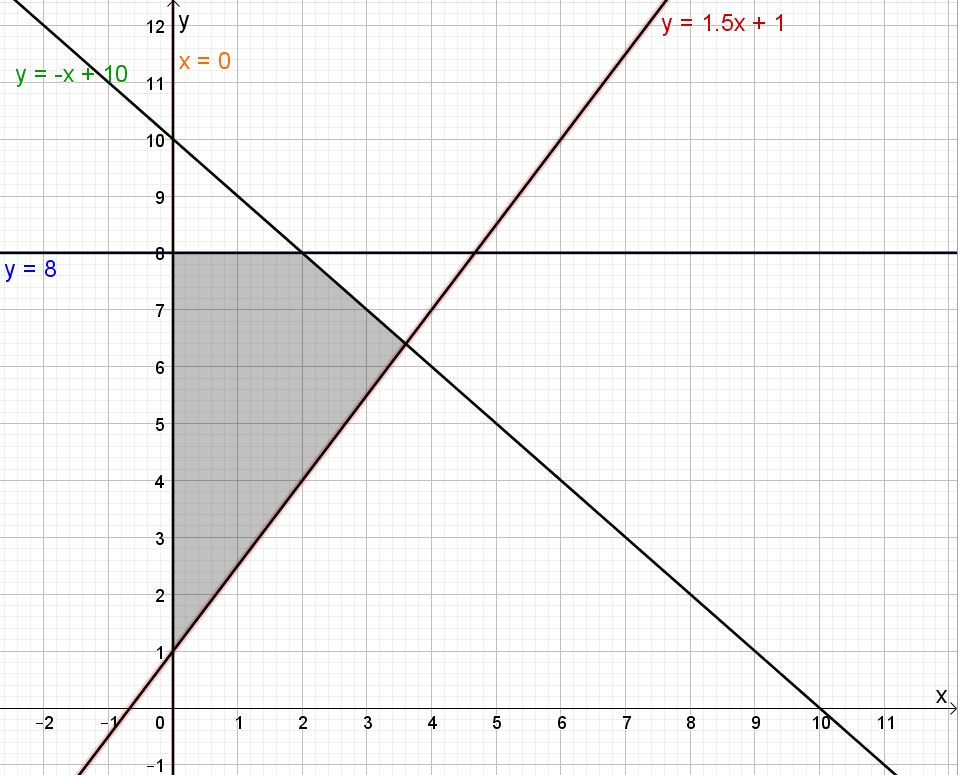
Vi har nå de fire ulikhetene:
Tegn de fire linjene
Oppgave 7
a)
Finner vertikal asymptote, som er den x-verdien som gir null i nevner, i dette tilfellet
Finner horisontal asymptote ved å la x gå mot uendelig.
Finner nullpunktet (dvs. skjæringspunktet med x-aksen):
Finner skjæringspunktet med y-aksen, som er det samme som konstantleddet, i dette tilfellet