Trigonometriske identiteter
Spisse vinkler
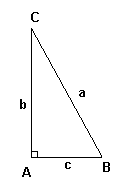
De trigonometriske funksjonene er sinus, cosinus, tangens. Vanligvis forkortes disse sin, cos, tan. For spisse vinkler defineres de trigonometriske funksjonene som forholdet mellom sidene i en rettvinklet trekant. Vi har:
DEFINISJONER
•
•
•
Enhetssirkelen - sin - cos - tan
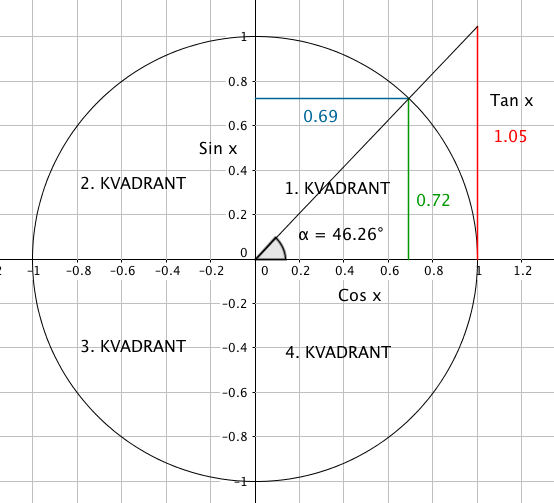
De trigonometriske funksjonene begrenser seg ikke til spisse vinkler. Vi tegner en sirkel med radius 1 der positive vinkler kan tenkes framkommet ved en dreining mot klokken og negative vinkler fremkommer ved dreining med klokken. Dette kalles orienterte vinkler. I enhetssirkelen ser vi på orienterte vinkler med absolutte vinkelmål (radianer). Enhetsirkelen legges med sentrum i origo i et ortonormert koordinatsystem, slik at et av vinkelbeina er sammenfallende med den positive x aksen. Det andre vinkelbeinet skjærer sirkelen i punktet (x,y). De trigonometriske funksjonene defineres som følger:
\\ \\ cot (a) = \frac xy \quad \quad sec (a) = \frac 1x \quad \quad cosec (a) = \frac 1y </math>
Sin og cos har alle perioden
Enhetssirkelen og dens fire kvadranter
Identiteter
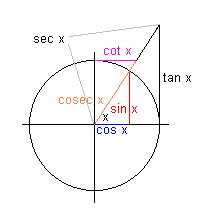
Geometrisk tolkning av de trigonometriske funksjonene. Figuren nedenfor viser de forskjellige trigonometriske funksjonene inntegnet i enhetssirkelen.
Definisjoner:
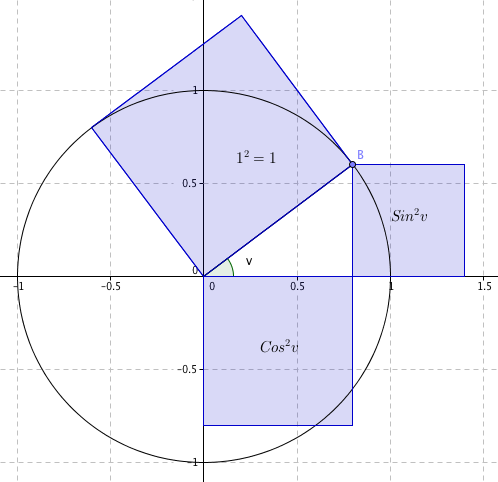
Det finnes mange trigonometriske identiteter. Her er noen av dem.
| Uttrykt ved | ||||||
|---|---|---|---|---|---|---|
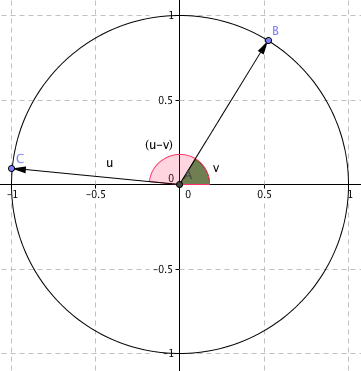
Sum og differanser av vinkler
Setter u = 0, cos 0 = 1 og sin 0 = 0:
Bruker (1) og (2) og får:
Dobble vinkler
Dersom u + v = 180° har vi at Sin v = sin u og cos v = -cos u
Flere funksjoner
Nedenfor følger en rekke trigonometriske identiteter. Noen er pensum i norsk skole (R2), andre ikke. Vi mener det er riktig å vise alle, da noen av dere kan komme til å studere i land der disse er pensum.
De tre neste er ikke pensum, men greie å kjenne til:
•
•
•
Ved observasjon ser vi at fortegnet til en trigonometrisk funksjon varierer avhengig av hvilken kvadrant man befinner seg i. Nedenfor følger en oversikt.
| Kvadrant | I | II | III | IV |
| cos | pos | neg | neg | pos |
| sin | pos | pos | neg | neg |
| tan | pos | neg | pos | neg |
| cot | pos | neg | pos | neg |
| sec | pos | neg | neg | pos |
| cosec | pos | pos | neg | neg |