S1 2016 vår LØSNING
Fasit (ikke løsning) laget av matteprat-bruker rekel
Løsning laget av matteprat-bruker LektorH
DEL EN
Oppgave 1
a)
$X^2-3X+2=0 \\ X= \frac{3 \pm \sqrt{9-8}}{2} \\ x=1 \vee x=2$
b)
$lg(4x+3)= lg7 \\ 10^{lg(4x+3)} = 10^{lg7} \\ 4x+3 =7 \\ 4x=4\\ x=1$
Oppgave 2
a)
$(2x-3)^2 -3(x-2)^2 + (x-1)(x+1) = \\ 4x^2-12x+9-3(x^2-4x+4)+x^2-1= \\ 4x^2-12x+9-3x^2+12x-12+x^2-1= \\ 2x^2-4$
b)
$\frac{a^2b^3}{(a^3b)^{-2}} = \frac{a^2b^3}{a{-6}b^{-2}} = a^{2-(-6)}b^{3-(-2)}= a^8b^5$
Oppgave 3
a)
Omkrets: 2x + 2y = 11
Areal: xy=6
<math> \left[ \begin{align*}2x+2y=11\\ xy=6 \end{align*}\right] </math>
b)
<math> \left[ \begin{align*}2x+2y=11\\ xy=6 \end{align*}\right] </math>
<math> \left[ \begin{align*}x=\frac{11}{2}-y\\ xy=6 \end{align*}\right] </math>
$( \frac {11}{2}-y)y=6 \\ -y^2 + \frac{11}{2}y - 6 =0 \\ -2y^2+11y - 12 =0 $
$y = \frac{-11 \pm \sqrt{121 - 96}}{-4} \\ y= \frac{3}{2} \vee y =4$
Innsatt gir det løsninger $( \frac 32, 4) \wedge (4, \frac32 )$ som jo er samme rektangel.
Lenden på rektangelet er 4 og bredden er $\frac 32$.
Oppgave 4
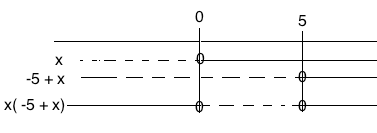
$-5x+x^2 \leq 0 \\ x(-5 + x) \leq 0$
$x \in [0, 5]$
Oppgave 5
a)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
$\binom{7}{4} = 35$
Teller ned til syvende rad (første rad er nullte rad), teller så fire mot høyre.
b)
Dersom man skal velge ut fire elementer fra en mengde på syv, uten tilbakelegging, kan det gjøres på 35 måter.
Oppgave 6
a)
b)
Oppgave 7
a)
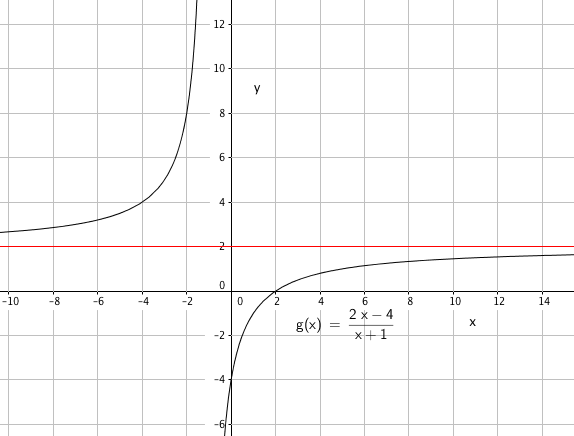
Vertikal asymptote for x= - 1 gir c = 1
Skjærer y akse i y = -4 gir g(0) = -4 som gir b = -4
Skjærer x aksen i x = 2 gir g(2) = 0 eller $2 \cdot 2 - 4 = 0$ som gir a=2
Funksjonsuttrykket blir da:
$g(x)= \frac{2x-4}{x+1}$
b)
Vertikal asymptote for x= -1
Horisontal asymptote finner vi ved å dele alle ledd i teller og nevner på x, for så å la x gå mot uendelig. Man ser at g går da mot 2. Atså er horisontal asymptote y = 2.
Oppgave 8
a)
b)
Oppgave 9
a)
Nullpunkt:
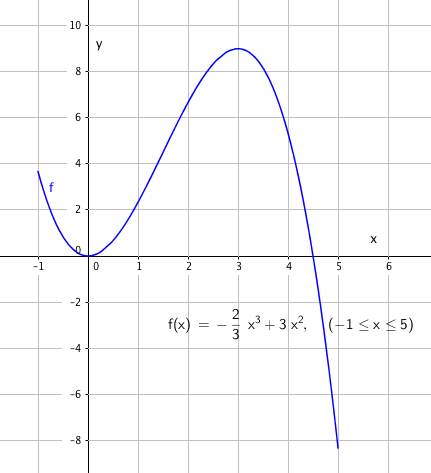
$f(x)=0 \\ - \frac 23 x^3 + 3x^2 =0 \\ x^2( - \frac23 x+3)= 0 \\ x = 0 \vee x = \frac 92$
Nullpunkter: $(0,0) \wedge ( \frac 92 , 0)$
b)
Ekstremalpunkter:
$f´(x)= -2x^2+6x \\ f´(x)=0 \\ -2x^2+6x=0 \\ x(-2x+6)=0 \\ x=0 \vee x=3$