1P 2015 vår LØSNING
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
a)
b)
Oppgave 2
a)
Vinklene i de to trekantene er parvis like, A = D, B = E og C = F , derfor er de to trekantene formlike.
b
Oppgave 3
Diagonalen i rektangelet er
Siden 9 ganger 9 er 81, bør det være fullt mulig å få den kvadratiske planten gjennom vinduet.
Oppgave 4
Areal av rektangel, minus de tre hvite trekantene blir:
Areal blått område:
Arealet av det skraverete området er 27 kvadratcentimeter.
Oppgave 5
a)
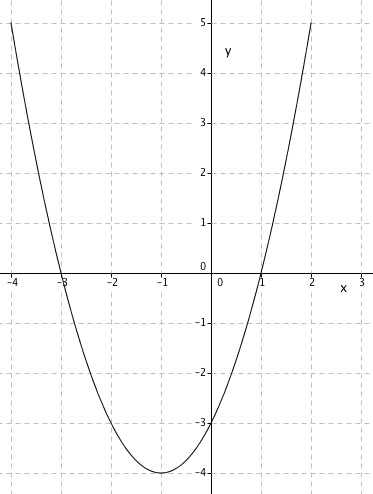
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| f(x) | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
b)
Oppgave 6
a)
P ( ikke "Jump") =
Det er fem tolvtedels sjanse for at du ikke tar en "Jump".
b)
En "Surf" og en "Catch" kan velges ut på to måter, først "Surf", så "Catch", eller motsatt:
P(en Surf og en Catch)=
Det er to nidels sannsynlighet for en av hver av de to.
Oppgave 7
Dersom varen følger indeksen vil den koste 8 kroner i 2014.
Oppgave 8
a)
b)
Oppgave 9
a)
Funksjonsuttrykk for rette linjer: y = ax + b
A:
Grafen begynner på 200 på y- aksen, når x ( antall kilometer er null). Det betyr at b = 200. Når x = 20 er y = 400. På 20 x enheter har y økt med 200. Det betyr at når x øker med en, øker y med 10. Da blir funksjonsuttrykket :
y = 10x + 200
B:
y= 5x + 800
b)
Dersom man kjører mindre enn 120 kilometer er firma A billigst. Firma B er billigst for kjørelengder over 120 kilometer.
c)
Nei. I både A og B er kilometerprisen større for de første kilometrene. Ved proporsjonalitet går grafen gjennom origo.
Oppgave 10
Siden boksene har samme høyde, vil boksen mdstørst grunnflate også ha størst volum.
Prisme: 7cm
Vi avrunder pi til 3,14.
Sylinder:
Det betyr at sylinderen har et større volum.
DEL TO
Oppgave 1
a)
Dersom 906 millioner utgjør ca 20% var den totale overføringen ca 4,5 milliarder før kutt. (
b)
UNICEF får redusert sin støtte med
Oppgave 2
a)
| Melk | Ikke melk | Total | |
| Juice | 110 | 206 | 316 |
| Ikke juice | 54 | 67 | 121 |
| Total | 164 | 273 | 437 |
b)
P( ikke melk) =
Dersom man trekker ut en tilfeldig elev ved skolen er det 62,5% sannsynnlig at vedkommende ikke drikker melk daglig.
c)
Vi trekker nå ut en telfeldig elev i gruppen som drikker melk daglig (164):
P (drikker juice | drikker melk) =
Det er ca. 67% sannsynlig at et elev drikker jucie hver dag, når vi vet at eleven drikker melk hver dag.
Oppgave 3
Oppgave 4
a)
b)
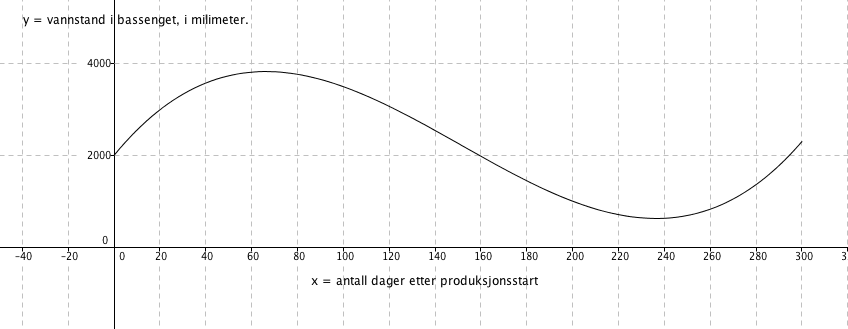
Oppgave 5
a)
b)
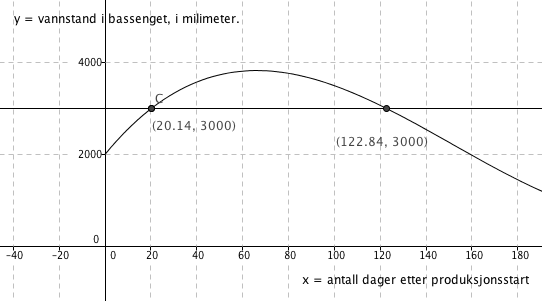
c)
På den 20 og 122 dagen er vannstanden 3000 milimeter. I tiden mellom disse dagene er den høyere.
d)
Oppgave 6
a)
b)
Oppgave 7
Målestokk:
Dette er jo en forstørrelse, i motsettning til tegninger og kart som er en forminskning. Målestokken er 1: 0,001 eller 1000:1.
Detbetyr at en meter på bildet er en milimeter i virkeligheten.
Oppgave 8
a)
b)
Oppgave 9
Volum av shylinder:
Radius i tanken er 2,44 dm