2P 2014 høst LØSNING

• Oppgaven
• Løsning som pdf

Oppgave 1

$ \frac{0,0003 \cdot 500000000}{0,002}= \frac{3 \cdot 10^{-4} \cdot 5 \cdot 10^{8}}{2 \cdot 10^{-3}} = \frac{3 \cdot 5}{2} \cdot 10^{-4+8-(-3)} = 7,5 \cdot 10^7$

Oppgave 2

$x \cdot 1,25 = 250 \\ x = \frac{250}{1,25} \\ x =200$

Varen kostet 200 kroner før den ble satt opp.

Oppgave 3

300m = 30000cm

Vi vet at 500 ark er 6 cm. Dersom vi deler 30000 på 6 finner vi antall bunker med 500 ark. Så ganger vi med 500 for å finne antall ark.

$ \frac{30000}{6} \cdot 500 = \frac{3 \cdot 10^4 \cdot 5 \cdot 10^2}{6 \cdot 10^0 } = 2,5 \cdot 10^6$

I en 300 meter høy bunke med ark vil det være 2 500 000 ark

Oppgave 4

$\frac{2^3 \cdot 2^0}{2} - 8 \cdot 2^{-2} = \\ 2^{3+0-1} - 2^3 \cdot 2^{-2} =\\ 4 - 2 = 2$

Oppgave 5

a)

Det er 15 år mellom 2014 0t 2029. I denne perioden minker elevtallet med 350 - 275 = 75 elever, dvs. 5 elever per år. En lineær modell blir da:

y = -5x + 350 , der x er antall år etter 2014. y er antall elever et gitt år.

b)

Elever i 2024, dvs. x= 10:

$ y = -5 \cdot 10 + 350 = 300$

Etter modellen i a vil det være ca. 300 elever.

c)

I 2014 er elevtallet 200.

Det forventes en årlig vekst i elevtallet på 3%, derfor vekstfaktor 1,03.

x er antall år etter 2014.

Oppgave 6

a)

$L(3) = 1500 \cdot 1,08^3$

1500 er startverdi.

1,08 er vekstfaktor for 8%.

3 er perioder fram i tid.

b)

$L(juli, august, september, oktober) = 1500 \cdot 1,08^{-2}+1500 \cdot 1,08^{-1} + 1500 \cdot 1,08^0 + 1500 \cdot 1,08^1$

Oppgave 7

a)

y aksen viser frekvens delt på klassebredde. 1,5. Klassebredden er 50 - 30 = 20. Vi får da:

$ \frac{x}{20} =1,5 \\ x = 1,5 \cdot 20 \\ x=30$

b)

Ved å bruke samme metode som i a, på de tre andre klassene finner man at det var 100 personer på kinoen. 10 av disse er mellom 0-10 år. Prosent er del av hundre, dvs. 10%.

Oppgave 9

a)

Det spilles 16 kamper: Det skåres i gjennomsnitt:

$\frac{0\cdot 2 +1 \cdot 6+ 2 \cdot 3 + 3\cdot 4 + 4 \cdot 1 }{16} = \frac{28}{16} = 1,75 $

Oda skårer i gjennomsnitt 1,75 mål per kamp.

b)

Den kummulative frekvensen for to mål er 11 ( 2 + 6 + 3). Det betyr at i 11 kamper skårer hun 2 mål eller mindre.

c)

Frekvensen for 3 mål er 4. Da er den relative frekvensen for 3 mål $ \frac{4}{16} = \frac{1}{4}$

d)

Hun skårer 4 mål i 25% av kampene. I 11 av 16 kamper skårer hun to mål eller mindre.

Oppgave 1

a)

Fra Excel får man:

23,5

26,1

18,4

22,8

25,1

20,3

22,7 Gjennomsnitt

2,652671609 Standardavvik

Gjennomsnittskastet er 22,7 meter, med et standardavvik på 2,65 meter.

b)

Hvem som er best kan vi ikke si noe om, men Sven kaster jevnere på lengdene enn Kjell, som har et standardavvik på 3,2 m.

Oppgave 2

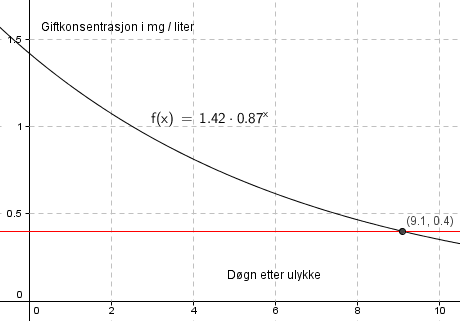
$f(x)= 1,42 \cdot 0,87^x$

a)

Rett etter ulykken er x=0, dvs. giftkonserntrasjonen er 1,42 mg / L.

Giftkonsentrasjonen minker med 1 - 0,87 = 0,13 = 13% per døgn.

b)

Gjennomsnittlig nedgang per døgn:

Rett etter ulykken: 1,42 mg /L.

Syv døgn etter ulykken: $ f(7)= 1,42 \cdot 0,87^7 = 0,54$ mg/L.

Gjennomsnitt per døgn (de første syv): $\frac{0,54 - 1,42}{7 } \approx -0,13$ mg/L.

Nedgangen var på ca 0,13 mg/liter i gjennomsnitt per døgn, de første syv døgn.

c)

Etter 9,1 dager er giften nede på 0,4 mg /L. Det kan nok være fornuftig å vente til dag 10 etter ulykken før man begynner å drikke det.

Oppgave 5

a)

Overflate = 2 kortsider + forside + tak

$O(x)= 2 \cdot h \cdot x + 4 \cdot h \cdot x + 4 \cdot x \cdot x \\ O(x)= 2hx+4hx+4x^2 \\ O(x)= 4x^2+6hx$

b)

Vi får beskjed om at O(x) = 40. Skal få h alene på venstre side.

$40 = 4x^2+6hx \\ 40 - 4x^2 = 6hx \\ 6hx= 40-4x^2 \\ h = \frac{40-4x^2}{6x} $

c)

En slik kasse kallles et prisme. Volumet av et prisme er

$V= Gh \\ V(x) = 4x^2h$

Nå har vi to variabler, x og h. Vi bytter h med uttrykket vi fant i b og får:

$V(x)= 4x^2 \cdot \frac{40-4x^2}{6x} \\V(x)= - \frac 83x^3+ \frac{80}{3}x $

Vi setter så funksjonsuttrykket inn i Geogebra og ser hvordan volumfunksjonen ser ut.