1T 2013 høst LØSNING
Diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1:
$7,5 \cdot 10^{12} \cdot 4,0 \cdot 10^{-4} = 30 \cdot 10^{12+(-4)} = 30 \cdot 10^8 = 3,0 \cdot 10^9$
Oppgave 2:
a)
| Blå bukser | Svarte bukser | Total | |
|---|---|---|---|
| Bukser som passer | $3$ | $3 $ | $6$ |
| Bukser som ikke passer | $1$ | $3$ | $4$ |
| Total | $4$ | $6$ | $10$ |
b)
P (buksa passer) =$\frac {6}{10}$ = 60%
Det er 60% sjanse for at buksa passer.
c)
P ( blå bukse, gitt at den passer) = $\frac 36 = \frac 12 = $ 50%
Det er 50% sjanse for at buksa er blå, når vi vet at hun har trukket en bukse som passer.
Oppgave 3:
$\frac {2x^2-18}{x^2+6x+9} = \frac {2(x+3)(x-3)}{(x+3)(x+3)} = \frac{2(x-3)}{x+3}$
Oppgave 4:
$ \frac{\sqrt 2 \cdot 2^0 \cdot 2^{-1}}{8^{\frac12} \cdot 2^{-2}} = \frac{2^{\frac 12} \cdot 2^{-1}}{2^{\frac 32}\cdot 2^{-2}} = \\ 2^{\frac12 -1-\frac32 + 2} = 2^0=1 $
Oppgave 5:
$2lgx-8=5lgx+1 \\ -3lgx =9 \\ lgx =-3 \\ x = 10^{-3} = 0,001$
Oppgave 6:
Rett linje: y = ax + b
stigningstal: $a = \frac{\Delta y}{\Delta x} = \frac{5-2}{3-1} = \frac 32$
Bruker dette sammen med første punkt og får:
$y=ax + b \\ 2= \frac 32 \cdot 1 + b \\ b= \frac 12$
Dvs:
$y = \frac 32x + \frac 12$
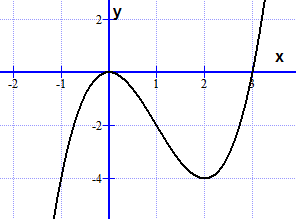
Oppgave 7:
Oppgave 8:
a)
b)
c)
Oppgave 9:
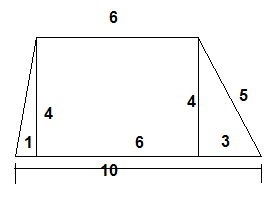
Oppgave 10:
Lengden av hypotenusen i den rettvinklede trekanten til venstre er $ \sqrt {4^2 + 1^2} = \sqrt {17}$ . omkretsen blir derved 10 + 5 + 6 + $ \ sqrt{17} = 21 + \sqrt{17}$ .