Røtter og potenser med brøkeksponent
Kvadratrot
Kvadratroten av et tall m, er et tall n som ganget med seg selv gir m, og skrives <tex> \sqr{m} </tex>
Hva er kvadratroten av 4? Tallet som ganget med seg selv gir 4 er 2. Det skrives slik:
<tex>\sqr{4}= \sqr{2 \cdot 2} = 2 </tex>
Mer generelt: dersom n·n = m så er: <tex>\sqr{m}= \sqr{n \cdot n} = n </tex>
Man kan ikke ta kvadratroten av et negativt tall.
Ut fra navnet kvadratrot er det naturlig å tro et det er en sammenheng mellom kvadratrot og kvadrat. La oss se!
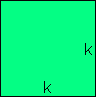
Et kvadrat har sidekanter med lengde k.
Arealet av kvadratet er k · k, eller k <tex>^2</tex>. Dersom man setter k = 10 cm betyr det at arealet av kvadratet er 100cm <tex>^2</tex>. Dersom man kjenner arealet av et kvadrat kan vi bruke kvadratroten til å finne lengden av sidekantene. Et kvadrat med areal 81 cm <tex>^2</tex> har sidekanter med lengde:
<tex>L = \sqrt{81cm^2}=9cm</tex>
Kvadratroten kalles av og til for andreroten og kan også skrives slik:
<tex> \sqrt{x}=\sqrt[2]{x}</tex>
Det er nyttig å vite dette, men man bruker <tex> \sqrt{x}</tex> når man ønsker å skrive kvadratroten av x.
n'terot
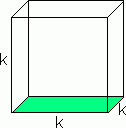
På samme måten som man kan ta kvadratroten, eller andreroten av at tall, er det også mulig å ta tredjeroten. Tenk deg en terning med sidekanter k. Vi setter k = 5cm. Volumet av terningen blir V = k3=k · k · k = 5cm · 5cm · 5cm = 125cm3.
Tredjeroten, eller kubikkroten som den også kalles, kan man bruke til å finne sidekanten av en terning dersom man kjenner volumet. Eksemplet over løser man på følgende måte:
Når man skal finne tredjeroten jakter vi på det tallet som, ganget med seg selv tre ganger, har et produkt tilsvarende tallet under rottegnet. Vi kan skrive et generelt utrykk slik:
Her må n være et helt positivt tall. Dersom n = 2 (kvadratrot) pleier vi utelate 2 - tallet.
Rot som potens
Regneregler
Et kvadrat har si
dekanter med lengde k.
Arealet av kvadratet er k · k, eller k2. Dersom man setter k = 10 cm betyr det at arealet av kvadratet er 100 cm2. Dersom man kjenner arealet av et kvadrat kan vi bruke kvadratroten til å finne lengden av sidekantene. Et kvadrat med areal 81cm2 har sidekanter med lengde:
Kvadratroten kalles av og til for andreroten og kan også skrives slik:
På samme måten som man kan ta kvadratroten, eller andreroten av at tall, er det også mulig å ta tredjeroten. Tenk deg en terning med sidekanter k. Vi setter k = 5cm. Volumet av terningen blir V = k3=k · k · k = 5cm · 5cm · 5cm = 125cm3.
Tredjeroten, eller kubikkroten som den også kalles, kan man bruke til å finne sidekanten av en terning dersom man kjenner volumet. Eksemplet over løser man på følgende måte:
Når man skal finne tredjeroten jakter vi på det tallet som, ganget med seg selv tre ganger, har et produkt tilsvarende tallet under rottegnet. Vi kan skrive et generelt utrykk slik:
Her må n være et helt positivt tall. Dersom n = 2 (kvadratrot) pleier vi utelate 2 - tallet.
| REGEL | EKSEMPEL |
| <tex>a^{\frac{m}{n}= \sqrt[n]{a^m} = (\sqrt[n]{a})^m</tex> |
<tex>27^{\frac{2}{3}}= \sqrt[3]{27^2} = (\sqrt[2]{27})^2 = 3^2 = 9</tex> |
| <tex>(ab)^{\frac1n}=\sqrt[n]{a \cdot b} =\sqrt[n]{a}\cdot \sqrt[n]{b} </tex> | <tex>(16x^8)^{\frac14}=\sqrt[4]{16 \cdot x^8} =\sqrt[4]{16}\cdot \sqrt[4]{x^8} =\sqrt[4]{2 \cdot 2\cdot 2 \cdot2}\cdot \sqrt[4]{x \cdot x \cdot x\cdot x\cdot x \cdot x \cdot x \cdot x} = 2x^2</tex> |
| <tex>( \frac ab)^{\frac 1n} =\sqrt[n]{\frac ab}= \frac{\sqrt[n]{a}}{\sqrt[n]{a}} </tex> | <tex>( \frac {8}{27})^{\frac 13} =\sqrt[3]{\frac {8}{27}}= \frac{2}{3} </tex> |
NB:I (10) er m og n positive heltall. I (9) er b forskjellig fra null.